빗물

문제

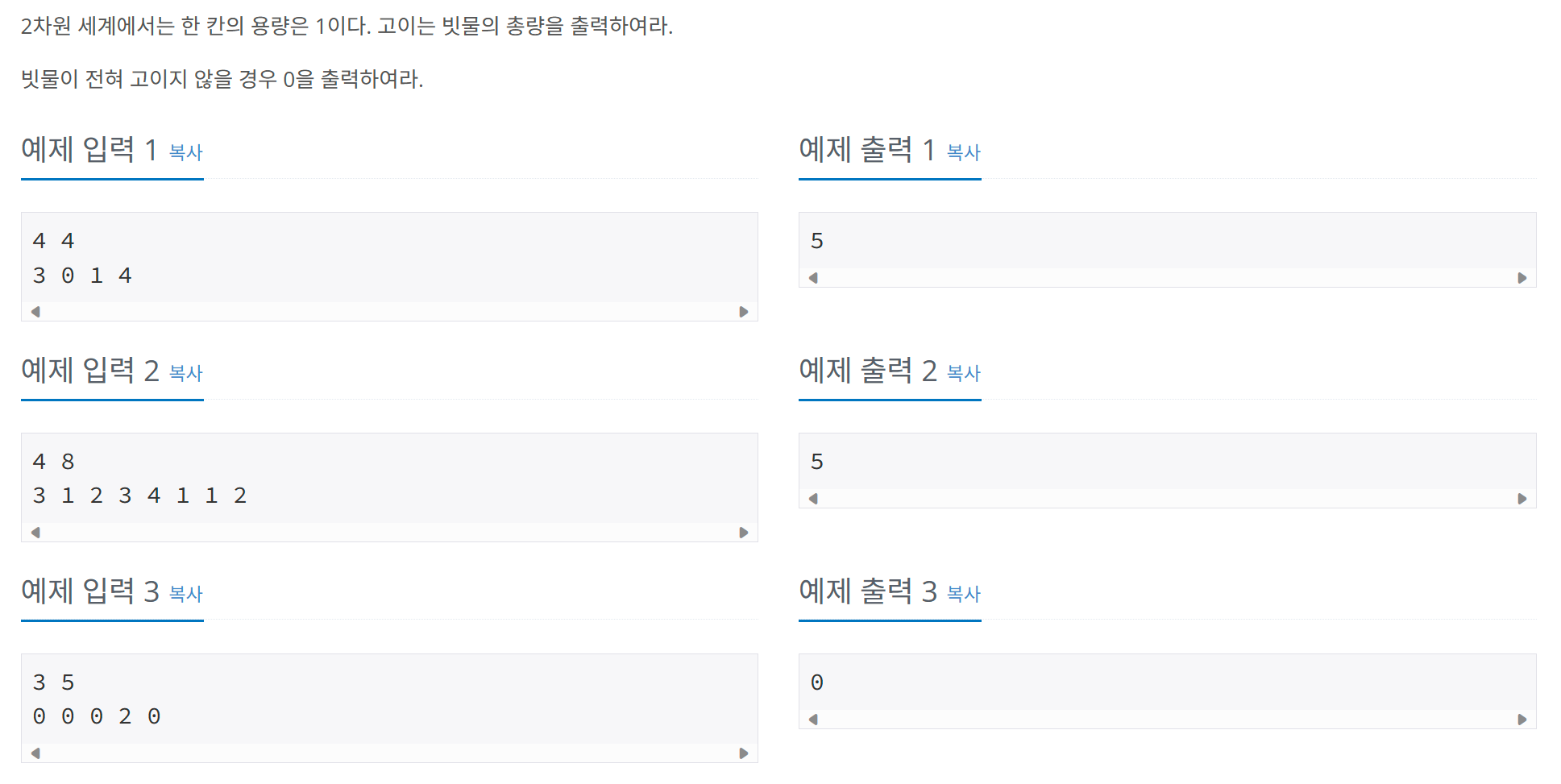
나의 풀이

1. 최대 높이 찾기

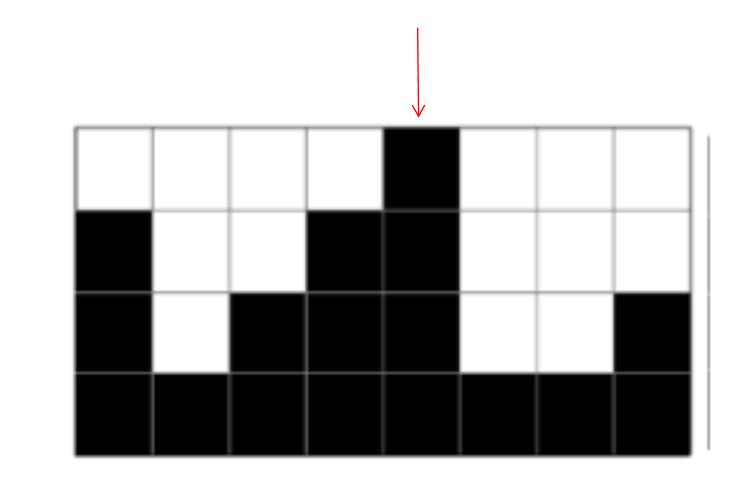
[3 1 2 3 4 1 1 2]에서 최대값은 4인 것을 알 수 있다.

2. 최대 높이 기준 왼쪽에서 최대 높이 찾기

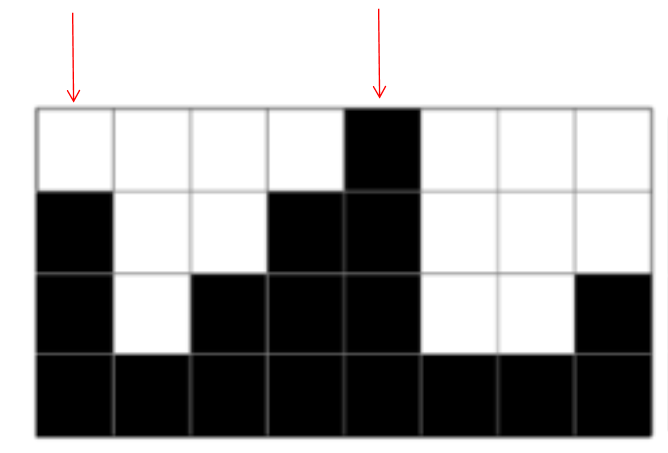
[3 1 2 3]에서 최대값은 3인 것을 알 수 있다.
3이 다른 인덱스에도 나오지만 먼저 나온 0번째 인덱스인 3 기준으로 한다.
이제 화살표 사이에 있는 블록들의 고이는 양을 계산할 수 있게 된다.
min(3, 4) -1, min(3, 4) - 2가 고일 것이다.

3. 반복

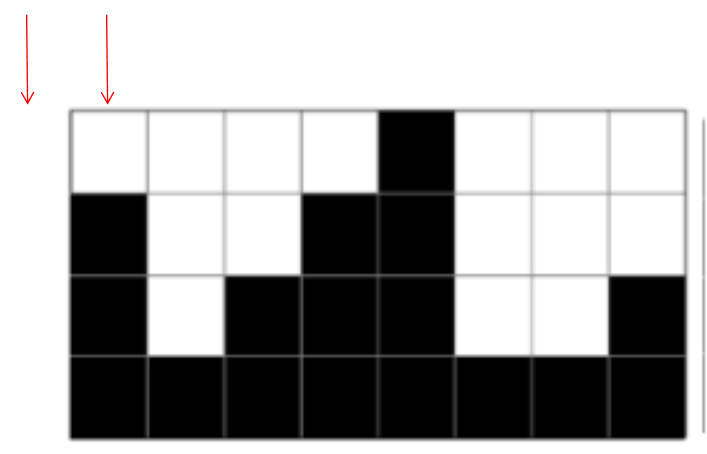
다음 왼쪽에 최대값을 찾으려 했지만 범위를 벗어나므로 왼쪽은 끝이난다.
오른쪽도 같은 방법대로 해주면 된다.

4. 최대 높이 기준 오른쪽에서 최대 높이 찾기

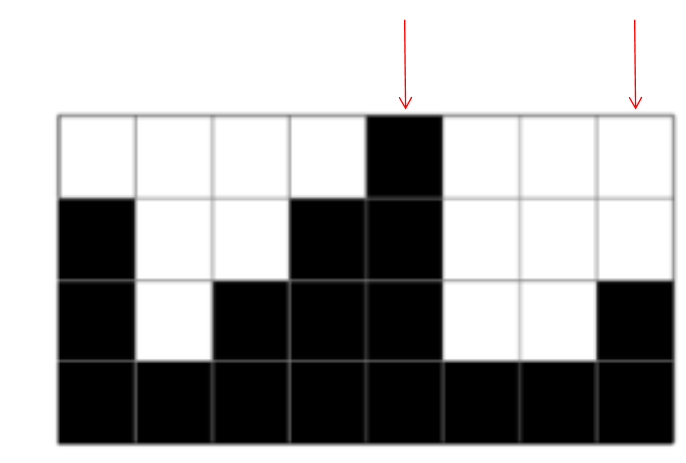
[1 1 2]에서 최대값은 2인 것을 알 수 있다.
이제 최대값4와 최대값 2 사이에 빗물이 고인다는 것을 알 수 있고 계산 또한 할 수 있다.
min(4, 2) - 1 min(4, 2) - 1가 고일 것이다.

5. 반복

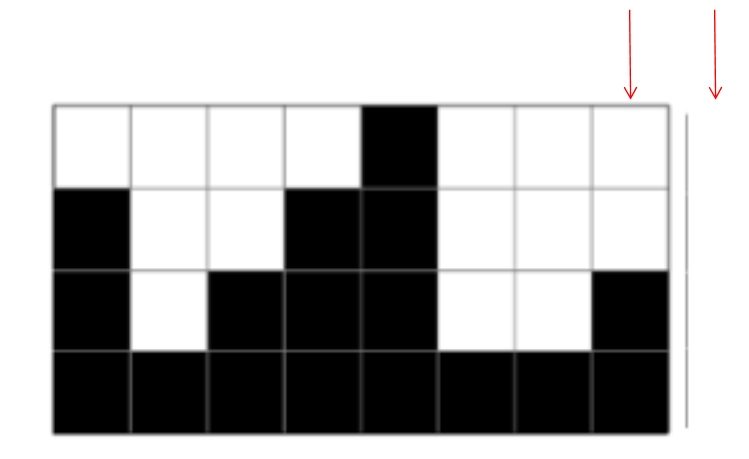
범위를 벗어나므로 끝이난다.

def solution():
    h, w = map(int, sys.stdin.readline().split())
    graph = list(map(int, sys.stdin.readline().split()))
    ans = 0
    def left(max_idx):
        nonlocal ans
        left_max_idx = -1
        max_num = 0
        for idx in range(max_idx):
            if max_num < graph[idx]:
                max_num = graph[idx]
                left_max_idx = idx

        if left_max_idx == -1:
            return

        if left_max_idx == -1:
            return

        num = min(graph[left_max_idx], graph[max_idx])
        for idx in range(left_max_idx + 1, max_idx):
            ans += (num - graph[idx])

        left(left_max_idx)

    def right(max_idx):
        nonlocal ans
        right_max_idx = -1
        max_num = 0
        for idx in range(max_idx+1, len(graph)):
            if max_num < graph[idx]:
                max_num = graph[idx]
                right_max_idx = idx

        if right_max_idx == -1:
            return

        num = min(graph[right_max_idx], graph[max_idx])
        for idx in range(max_idx + 1, right_max_idx + 1):
            ans += (num - graph[idx])

        right(right_max_idx)

    max_idx = -1
    max_num = 0
    for idx in range(len(graph)):
        if max_num < graph[idx]:
            max_num = graph[idx]
            max_idx = idx

    left(max_idx)
    right(max_idx)

    print(ans)
solution()

처음 max_idx로 가장 최대값 인덱스를 찾는다.
기 최대값 인덱스 기준으로 left, right함수를 호출하여 빗물에 고인 양을 찾는다.
2개의 함수의 로직은 앞서 설명한 로직으로 실행된다.

다른 풀이

일단 가장 양 옆에 있는 부분은 물을 고일 수 없으므로 range는 1 ~ len(graph) - 1로 해준다.
또한 특정 위치에서 고이려면 특정 위치 기준으로 양 옆에 더 높은 블록이 있어야 한다.
양 옆에 가장 높은 블록 변수 left_max, right_max가 존재한다.
그리고 이 둘 중 작은 것 기준으로 담기게 되므로 base라는 변수를 둔다.
base가 현재 위치 블록 보다 높아야지 잠기므로 조건문을 추가한다.

def solution():
    h, w = map(int, sys.stdin.readline().split())
    graph = list(map(int, sys.stdin.readline().split()))

    ans = 0

    for i in range(1, len(graph) - 1):
        left_max = max(graph[:i])
        right_max = max(graph[i+1:])

        base = min(left_max, right_max)

        if base - graph[i] > 0:
            ans += base - graph[i]
    print(ans)
solution()