BST(이진 검색 트리)
이진 검색 트리는 다음과 같은 특징을 가진다.
1. 각 노드에 중복되지 않는 키(key)가 있다.
2. 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다.
3. 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다.
4. 좌우 서브 트리도 모두 이진 탐색 트리여야 한다.
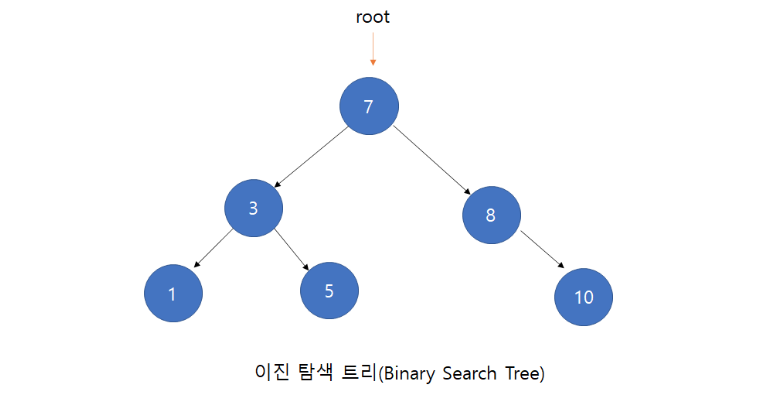
위에 이미지를 보게 되면 7보다 작은 값은 왼쪽 서브트리에, 큰 값은 오른쪽 서브트리에 존재한다.
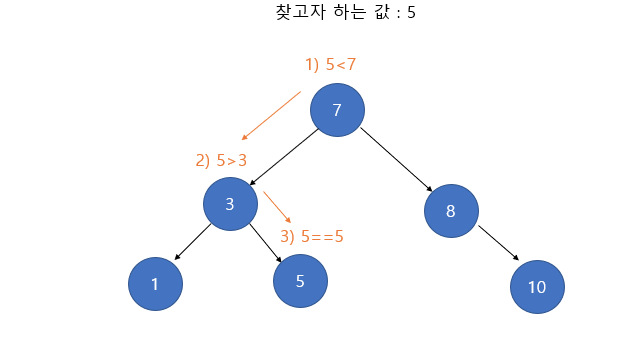
BST(이진 검색 트리)탐색
- 루트 노드의 키와 찾고자 하는 값을 비교한다. 찾고자 하는 값이라면 탐색을 종료한다.
- 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행한다.
- 찾고자 하는 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리로 탐색한다.
위 과정을 찾고자 하는 값을 찾을 때까지 진행한다. 만약 값을 찾지 못하면 그대로 종료한다.
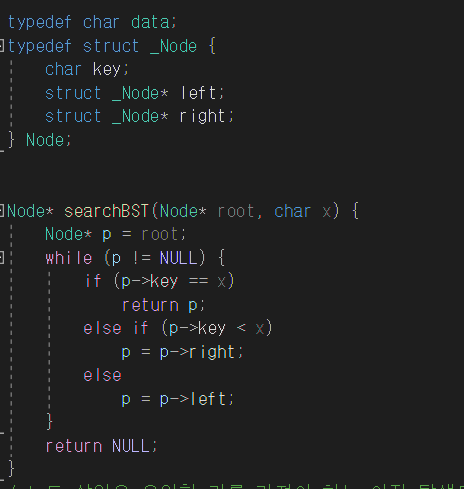
포인터 변수 p에 root포인터를 저장한다. 그리고 찾고자 하는 값 x와 p의 키 값과 비교하여 작으면 left를 크면 right로 탐색한다. 탐색하다가 p값이 null될 때가 있다. 해당 x값은 없다는 의미로 null을 리턴한다.
BST(이진 검색 트리)삽입
- 넣으려는 값이 탐색 시 존재한다면 오류를 발생한다. (중복 값 허용 x)
- 탐색 실패시 해당 위치에 넣으려는 값을 넣는다.
Node* insertBST(Node* root, char x) {
Node* p = root;
Node* parent = NULL;
while (p != NULL) {
parent = p;
if (p->key == x) {
printf("같은 키가 있습니다.\n");
return p;
}
else if (p->key < x)
p = p->right;
else
p = p->left;
}
//새 노드 할당.
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->key = x;
newNode->left = newNode->right = NULL;
//parent의 자식으로 새 노드 붙이기.
if (parent != NULL) {
if (parent->key < newNode->key)
parent->right = newNode;
else
parent->left = newNode;
}
return newNode;
}parent 변수를 만든다. 그 이유는 현재 노드를 기준으로 부모 노드 위치를 알아야 부모노드 left, right 포인터에 새로 만든 포인터를 연결할 수 있기 때문이다.
탐색 함수와 비슷하게 현재 포인터 위치인 p를 root노드로 치환한다.
그 후 x를 탐색하고 만약 해당하는 x가 존재한다면 빠져나간다. 탐색하다가 더 이상 존재하지 않아 p값이 NULL이 된다면 그 자리에 새 노드를 할당해야 한다.
넣으려는 값 x를 새 노드의 키값으로 둔다.
이제 넣으려는 값을 부모노드에 연결시키면 되는데 부모 노드는 parent에 할당되어 있다. parent의 키값이 x보다 크다면 오른쪽에 그렇지 않다면 왼쪽에 연결시키면 된다.
BST(이진 검색 트리)삭제
이진 검색 트리 삭제 할 때에는 3가지 상황을 나누어 구현해야 한다.
1. 삭제하려는 노드가 단말 노드인 경우
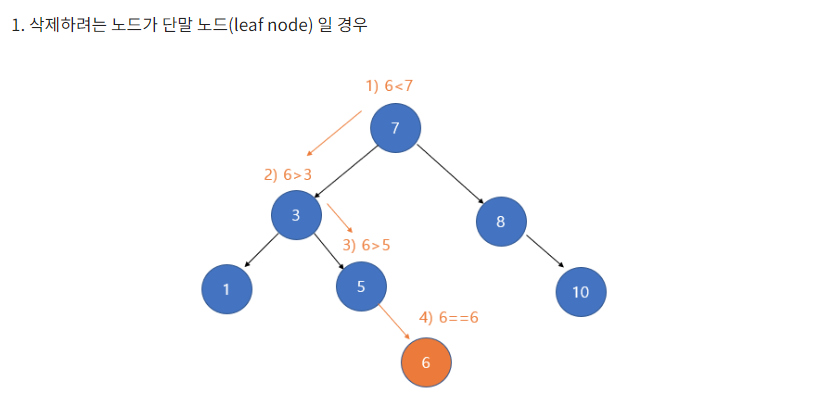
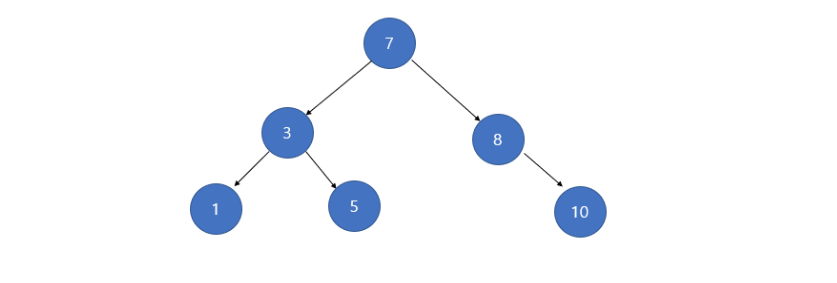
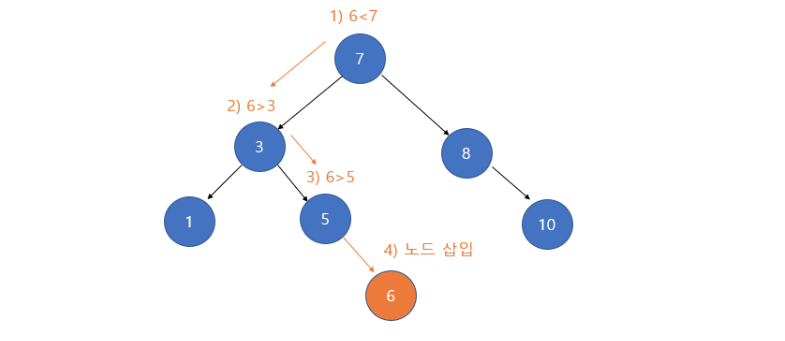
만약 6을 삭제하려 하면
마찬가지로 6을 탐색하고 탐색한 6을 끊어 버리면 된다.
Node* p = root;
Node* parent = NULL;
while ((p != NULL) && (p->key != x)) {
parent = p;
else if (p->key < x)
p = p->right;
else
p = p->left;
}
if (p == NULL) {
printf("찾는 노드가 없습니다.");
return root;
}
//차수가 0인 경우
if (p->left == NULL && p->right == NULL) {
if (parent == NULL)
root = NULL;
else {
if (parent->left == p)
parent->left = NULL;
else
parent->right = NULL;
}
}처음에는 탐색을 한다. 하지만 추가적인 부분이 있다. 즉 while문 조건을 보면 기존에 p != NULL (더 이상 탐색이 안 될경우) 뿐만 아니라 x가 찾아진다면 종료한다. 따라서 p == NULL이면 탐색된 것이 없으므로 리턴해준다.
차수가 0일 때에는 left, right 둘다 NULL 이다. 이 때에는 2가지 경우를 나눈다.
1. 삭제하려는 노드가 바로 root에 있고 차수가 0일 때
이 때에는 그냥 root를 NULL로 하면 된다.
2. 삭제하려는 노드가 root에 있지 않고 차수가 0일 때
만약 부모노드 left가 p라면 left를 null로 해주고 그렇지 않다면 right를 null해준다.
2. 삭제하려는 노드의 서브 트리가 하나인 경우(왼쪽 혹은 오른쪽 서브 트리)
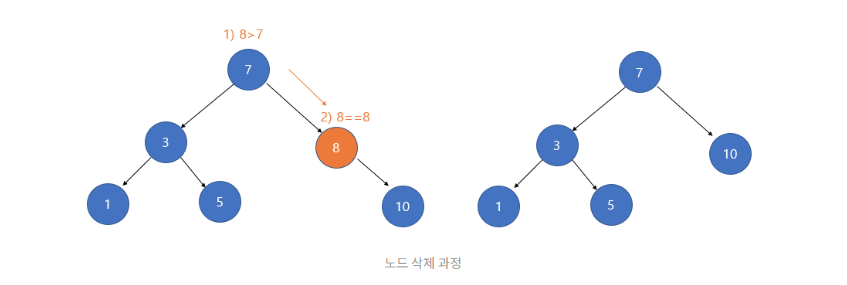
삭제할 노드의 자식 노드를 삭제할 노드의 자식 노드를 삭제할 노드의 부모 노드가 가리키게 하고 해당 노드를 삭제한다.
//차수가 1인 경우
else if (p->left == NULL || p->right == NULL) {
Node* child = (p->left != NULL) ? p->left : p -> right;
if (parent == NULL)
root = child;
else {
if (parent->left == p)
parent->left = child;
else
parent->right = child;
}
}현재 탐색 된 포인터 p의 left자식노드 또는 right 자식노드가 있다면 1개만 있다고 할 수 있다.
child 변수를 설정하는데 이 변수에는 현재 탐색도니 포인터 p에 존재하는 자식 노드의 포인터를 저장한다.
마찬가지로 2가지를 나누어서 생각해야한다.
1. 현재 탐색된 포인터 p가 root일 때
root노드를 p의 자식노드로 바꾸면 된다.
2. 그렇지 않다면
부모노드에 자식노드를 연결한다.
3. 삭제하려는 노드의 서브트리가 두 개인 경우
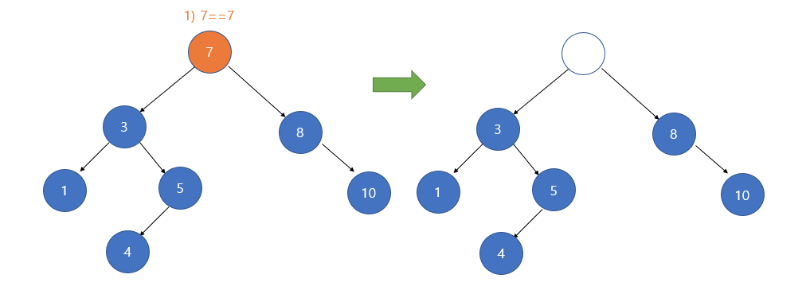
삭제할 때에 삭제된 노드에 하나의 노드를 할당해야 하는데 2가지 방법이 있다.
-
삭제할 노드의 왼쪽 서브 트리의 가장 큰 자손을 해당 노드의 자리에 올린다.
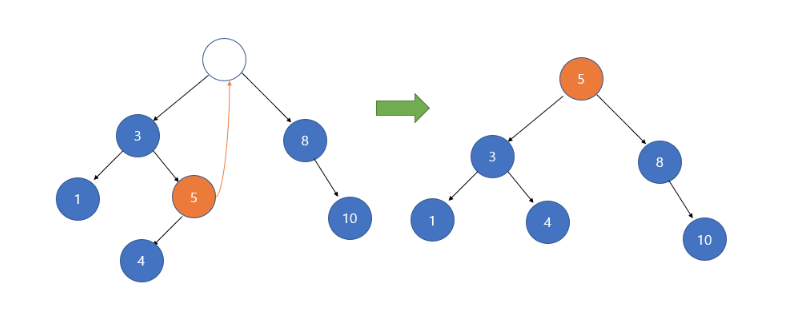
왼쪽 서브 트리에서 오른쪽으로만 탐색하게 되면 5에서 멈춘다. -
삭제할 노드의 오른쪽 서브 트리의 가장 작은 자손을 해당 노드의 자리에 올린다.
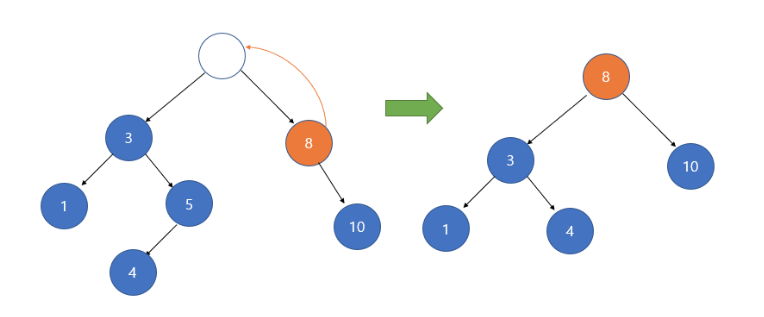
오른쪽 서브 트리에서 왼쪽으로만 탐색하게 되면 8에서 멈춘다.
//차수가 2인 경우
else {
Node* succ_parent = p;
Node* succ = p->right;
while (succ->left != NULL) {
succ_parent = succ;
succ = succ->left;
}
p->key = succ->key;
if (succ_parent->left = succ)
succ_parent->left = succ->right;
else
succ_parent->right = succ->right;
p = succ;
}
free(p);
return root;통상적으로 오른쪽 서브 트리에서 가장 작은 값을 계승자로 한다.
가장 작은 값을 찾기 위해선 왼쪽으로 찾으면 된다.
succ_parent에는 현재 삭제할 node의 포인터값이, succ에는 오른쪽 서브 트리에 포인터값이 저장된다.
가장 작은 값을 찾기 위해선 succ의 left값이 NULL일 때를 보면 되는데 NULL이라면 succ값이 가장 작은 값이 된다.
그래서 삭제할 p포인터 key값을 가장 작은 값으로 바꾼다.
맨 처음 root에서 무조건 right로 가야 한다. 그 때 root포인터값이 succ가 될 수 있다. 이 때를 대비해 다음과 같은 조건문을 추가한다.
전체코드
#include <stdio.h>
#include <stdlib.h>
typedef char data;
typedef struct _Node {
char key;
struct _Node* left;
struct _Node* right;
} Node;
Node* searchBST(Node* root, char x) {
Node* p = root;
while (p != NULL) {
if (p->key == x)
return p;
else if (p->key < x)
p = p->right;
else
p = p->left;
}
return NULL;
}
/*노드 삽입은 유일한 키를 가져야 하는 이진 탐색트리에는 탐색이 성공했을 때는 삽입이 당연히 안된다.*/
/*탐색 실패 시 실패한 위치에 노드 삽입한다.*/
Node* insertBST(Node* root, char x) {
Node* p = root;
Node* parent = NULL;
while (p != NULL) {
parent = p;
if (p->key == x) {
printf("같은 키가 있습니다.\n");
return p;
}
else if (p->key < x)
p = p->right;
else
p = p->left;
}
//새 노드 할당.
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->key = x;
newNode->left = newNode->right = NULL;
//parent의 자식으로 새 노드 붙이기.
if (parent != NULL) {
if (parent->key < newNode->key)
parent->right = newNode;
else
parent->left = newNode;
}
return newNode;
}
/*노드 삭제는 3가지 방법으로 나누어서 삭제
1.차수가 0일 때 해당 노드만 free시키고 해당 노드로 향하는 parent 포인터만 null값으로 바꿔 주면 된다.
*/
Node* deleteBST(Node* root, char x) {
Node* p = root;
Node* parent = NULL;
while ((p != NULL) && (p->key != x)) {
parent = p;
if (p->key == x) {
printf("같은 키가 있습니다.\n");
return p;
}
else if (p->key < x)
p = p->right;
else
p = p->left;
}
if (p == NULL) {
printf("찾는 노드가 없습니다.");
return root;
}
//차수가 0인 경우
if (p->left == NULL && p->right == NULL) {
if (parent == NULL)
root = NULL;
else {
if (parent->left == p)
parent->left = NULL;
else
parent->right = NULL;
}
}
//차수가 1인 경우
else if (p->left == NULL || p->right == NULL) {
Node* child = (p->left != NULL) ? p->left : p -> right;
if (parent == NULL)
root = child;
else {
if (parent->left == p)
parent->left = child;
else
parent->right = child;
}
}
//차수가 2인 경우
else {
Node* succ_parent = p;
Node* succ = p->right;
while (succ->left != NULL) {
succ_parent = succ;
succ = succ->left;
}
p->key = succ->key;
if (succ_parent->left = succ)
succ_parent->left = succ->right;
else
succ_parent->right = succ->right;
p = succ;
}
free(p);
return root;
}
void Inorder(Node* root) {
if (root == NULL)
return;
Inorder(root->left);
printf("%c", root->key);
Inorder(root->right);
}
int main() {
Node* root = insertBST(NULL, 'D');
insertBST(root, 'I');
insertBST(root, 'F');
insertBST(root, 'A');
insertBST(root, 'G');
insertBST(root, 'C');
Inorder(root); printf("\n");
root = deleteBST(root, 'I');
Inorder(root); printf("\n");
return 0;
}