ACM Craft

ACM Craft

풀이

위상정렬

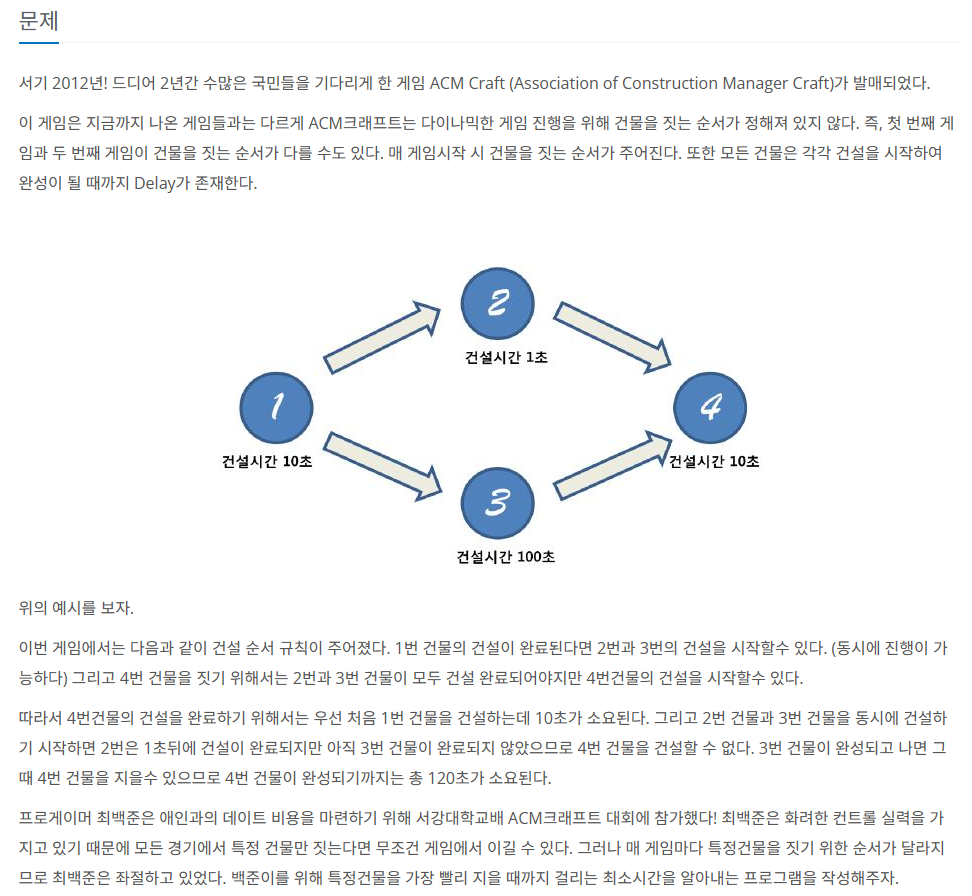
해당 인풋을 기준으로 위상정렬을 해보자
1 -> 0
2 -> 1
3 -> 1
4 -> 1
5 -> 1
6 -> 1
7 -> 2
8 -> 1
즉 from, to 기준으로 to로 들어오는 개수를 세준다.

개수가 0인 것을 기준으로 출발하면 시작할 수 있는 노드는 1말곤 없다.

1부터 시작하여 갈 수 있는 경로는 2, 3이 있다.
2, 3의 개수를 1감소 시킨다.
그리고 개수는 둘 다 0이 되므로 결국 2로 도달할 수 있는 모든 경로는 끝난 것이다. 이런식으로 진행하면 위상정렬로 조건을 만족하여 목표지점에 도달할 수 있다.

하지만 여기서 DP를 사용할 수 있다.
각 지점마다 최대값을 구해주면 되는 것이다.
만약 개수가 4이면 결국 경로는 4개가 될 것이고 이 4개 중에서 최대값을 저장해 DP로 풀면 된다.

import java.io.*;
import java.util.*;

public class Main {
	static int T, N, K;
	static int[] TIME;
	static HashMap<Integer, ArrayList<Integer>> graph;
	static int[] dp;
	static int[] count;
	
	public static void main(String[] args) throws IOException {
		//BufferedReader br = new BufferedReader(new FileReader("./input.txt"));
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());

		T = Integer.parseInt(st.nextToken());

		for (int t = 1; t <= T; t++) {
			st = new StringTokenizer(br.readLine());
			N = Integer.parseInt(st.nextToken());
			K = Integer.parseInt(st.nextToken());
			TIME = new int[N + 1];
			dp = new int[N + 1];
			count = new int[N + 1];
			graph = new HashMap<>();
			
			st = new StringTokenizer(br.readLine());
			for (int i = 1; i <= N; i++) TIME[i] = Integer.parseInt(st.nextToken());
			
			for (int i = 0; i < K; i++) {
				st = new StringTokenizer(br.readLine());
				
				int from = Integer.parseInt(st.nextToken());
				int to = Integer.parseInt(st.nextToken());
				
				if (graph.containsKey(from)) {
					ArrayList<Integer> list = graph.get(from);
					list.add(to);
					graph.put(from, list);
				} else {
					ArrayList<Integer> list = new ArrayList<>();
					list.add(to);
					graph.put(from, list);
				}
				
				count[to]++;
			}
			
			st = new StringTokenizer(br.readLine());
			int target = Integer.parseInt(st.nextToken());
			
			Deque<Integer> deque = new LinkedList<>();
			
			// init
			for (int i = 1; i <= N; i++) {
				if (count[i] == 0) {
					deque.add(i);
					dp[i] = TIME[i];
				}
			}
			
			while (!deque.isEmpty()) {
				int cur_node = deque.pollFirst();
				// 종료 조건
				if (count[target] == 0) break;
				
				if (!graph.containsKey(cur_node)) continue;
				
				ArrayList<Integer> new_list = graph.get(cur_node);
				
				for (int new_node : new_list) {
					dp[new_node] = Math.max(dp[new_node], dp[cur_node] + TIME[new_node]);
					
					count[new_node] -= 1;
					if (count[new_node] == 0) {
						deque.add(new_node);
					}
				}
			}
			
			System.out.println(dp[target]);
		}

	}
}