1914 하노이탑

문제

알고리즘

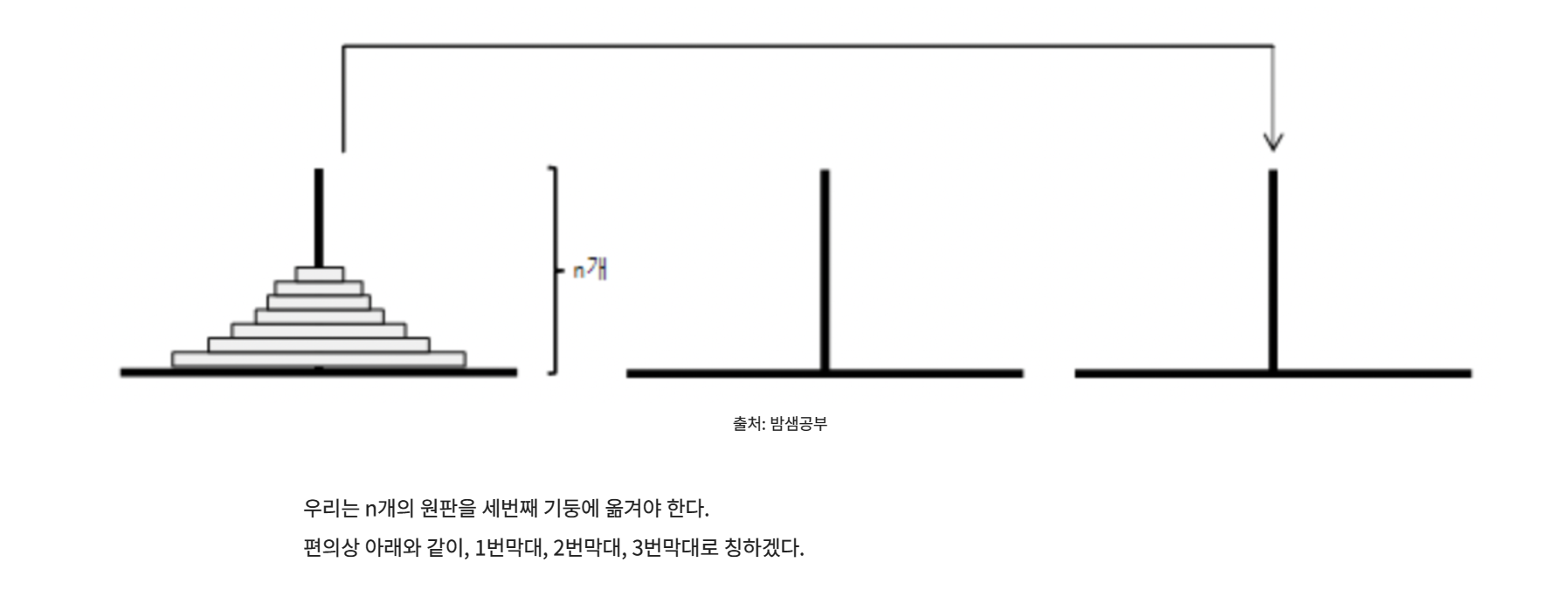
이렇게 구현하기 위해서 재귀함수를 사용해야 한다.

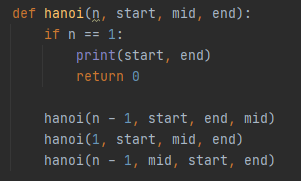
start => 시작지점
mid => 경유지점
end => 도착지점 이다.
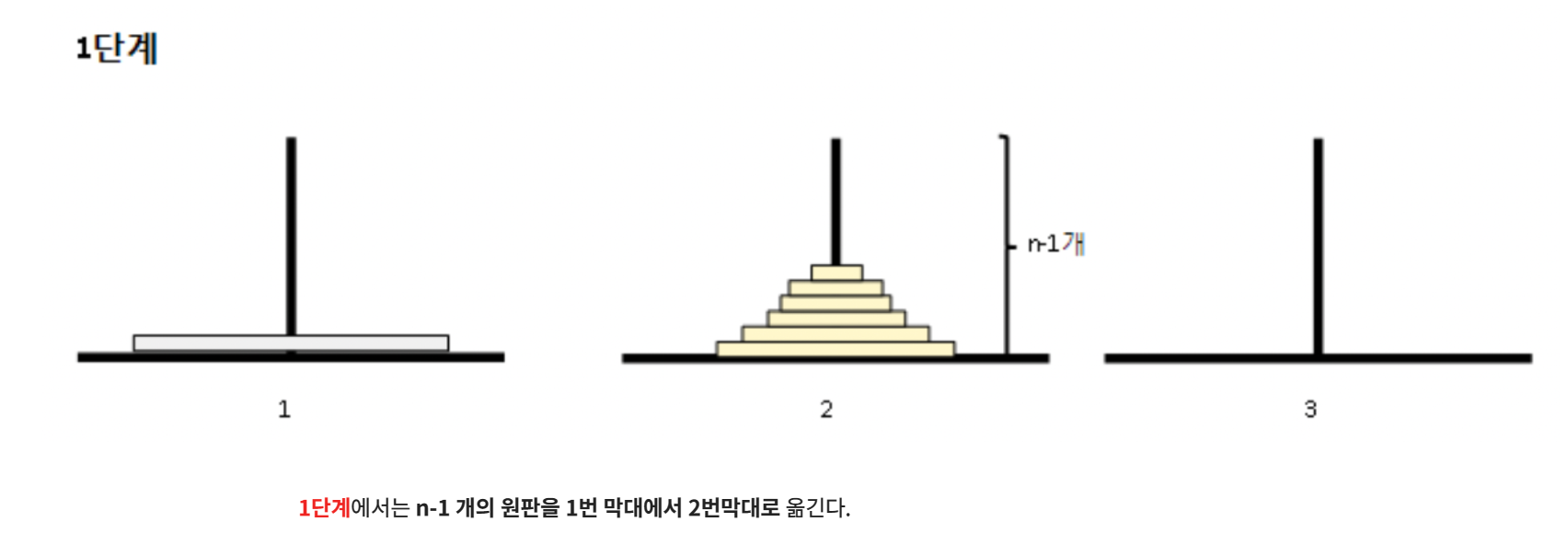
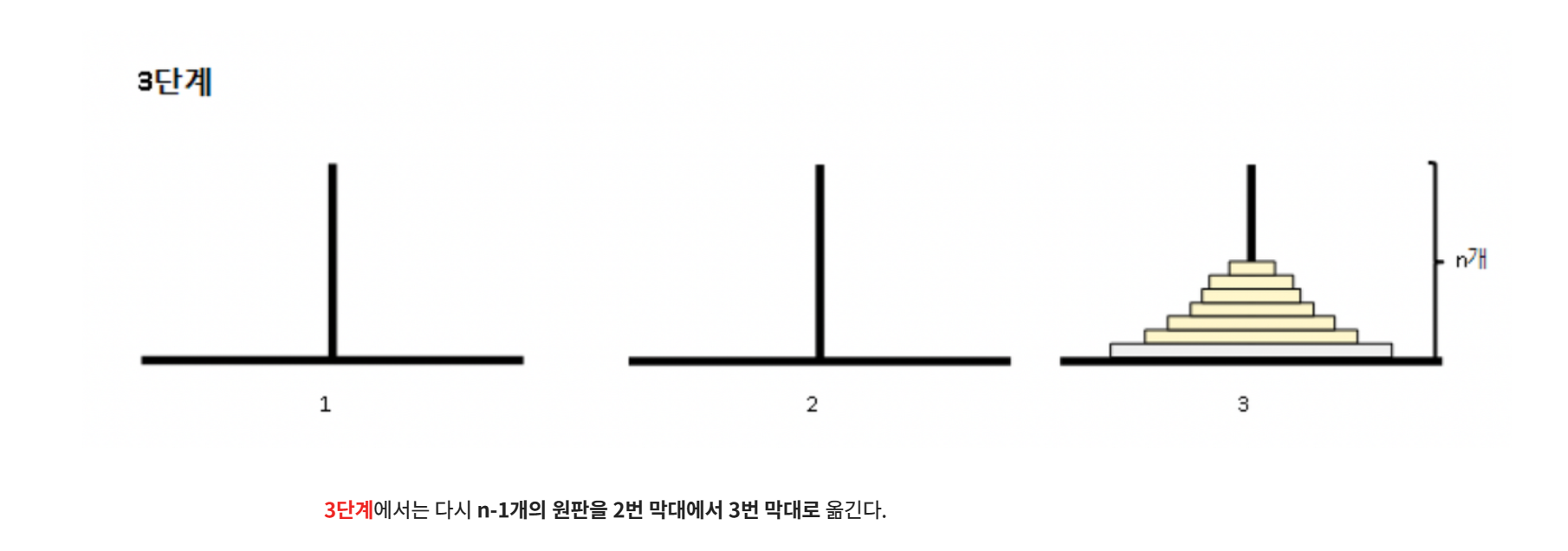
재귀함수를 통해 n-1개를 start지점에서 end지점을 경유해 mid지점으로 둔다. 그래야지 마지막 원판을 end지점에 놓을 수 있기 떄문이다.
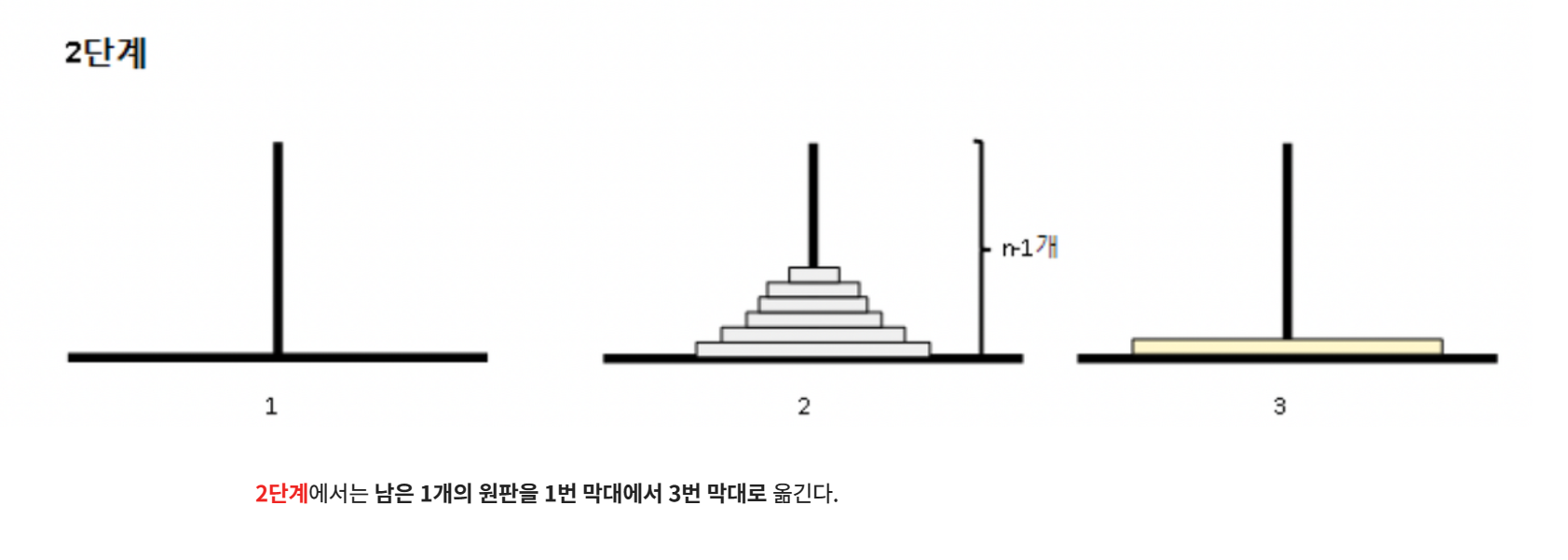
그 다음 start지점에는 가장 큰 원판이 남았을 것이므로 start에서 end로 옮겨준다.
이제 n-1개 원판을 mid 지점에서 start를 경유하여 end지점으로 보내면 된다.

내가 풀었던 코드

for test_case in range(1):
    num = int(sys.stdin.readline())

    q = deque()
    dp = {}
    def hanoi(n, start, mid, end):
        global  num
        ans = 0
        if n > 20 and (n, start, mid, end) in dp:
            return dp[(n, start, mid, end)]
        if n == 1:
            if num <= 20:
                q.append((start, end))
            return 1

        ans += hanoi(n-1, start, end, mid)
        ans += 1
        if num <= 20:
            q.append((start, end))
        ans += hanoi(n-1, mid, start, end)

        dp[(n, start, mid, end)] = ans
        return ans

    ans = hanoi(num,1,2,3)
    print(ans,)
    while q:
        x, y= q.popleft()
        print(x,y)

20개 이하만 과정을 출력하라고 명시했으므로 20개일 때만 q에 담아서 출력하는 방법으로 하였다. 이렇게 할 경우 시간초과가 발생하였다. 그래서 메모리제이션 기법을 사용하였는데 이렇게 하니 통과 되었다.

다른 방법

for test_case in range(1):
    n = int(sys.stdin.readline())


    def hanoi(n, start, mid, end):
        if n == 1:
            print(start, end)
            return 0

        hanoi(n - 1, start, end, mid)
        hanoi(1, start, mid, end)
        hanoi(n - 1, mid, start, end)

    print(2**n-1)
    if n<=20:
        hanoi(n, 1, 2, 3)

합은 금방 구할 수가 있었다.
n = 1 => 1
n = 2 => 2
n = 3 => 7
n = 4 => 15
...
즉 규칙적인 수가 나왔는데 이것을 공식으로 나타내면 2^n - 1이다.
이것으로 갯수는 알 수 있었고 n <= 20일 때만 출력하도록 하니 금방 나왔다.