1074 Z

✏️ 문제

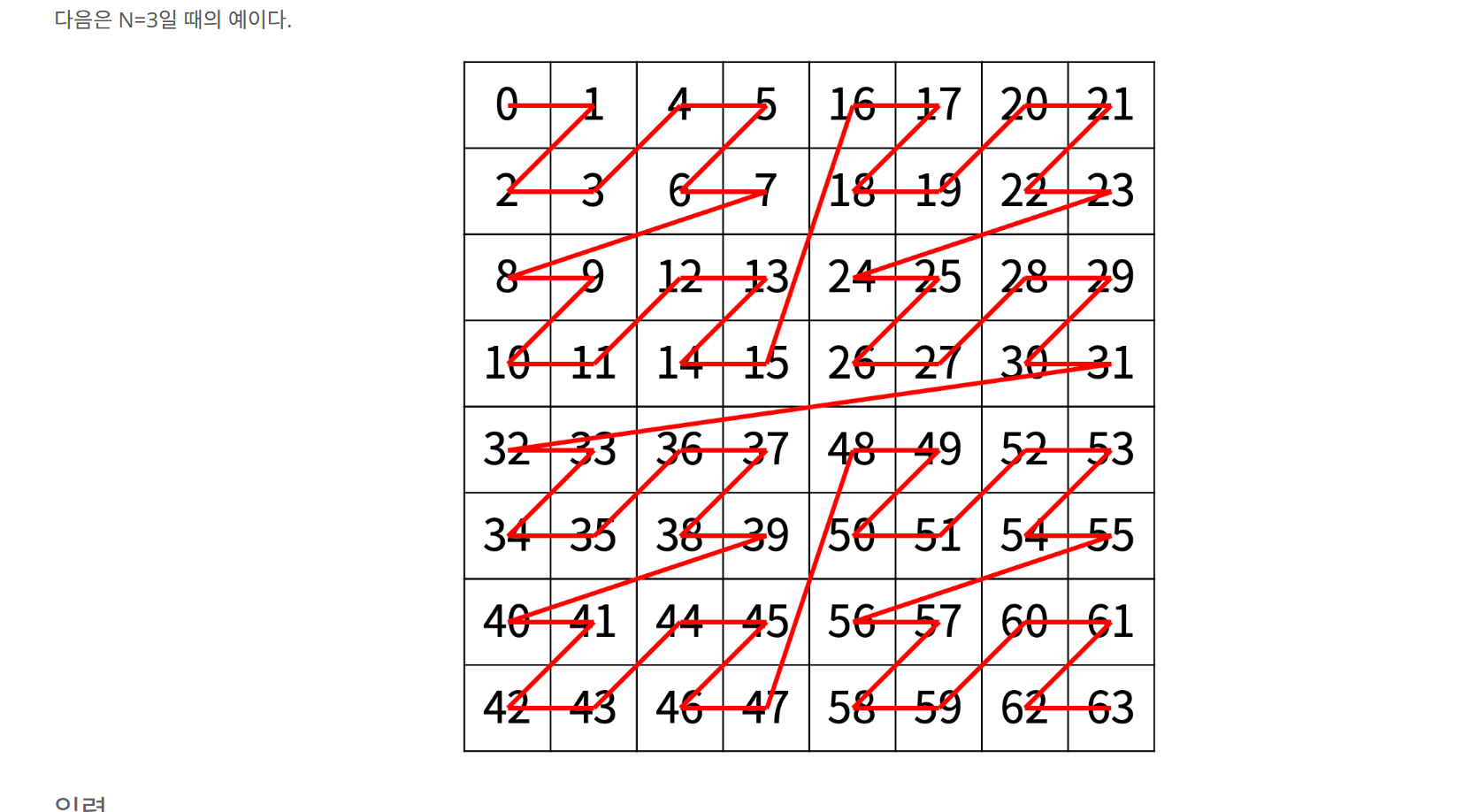
📝 처음 풀었던 풀이

이 문제는 전에 풀었던 쿼드트리 문제랑 비슷했다.
쿼드트리:https://www.acmicpc.net/problem/1992

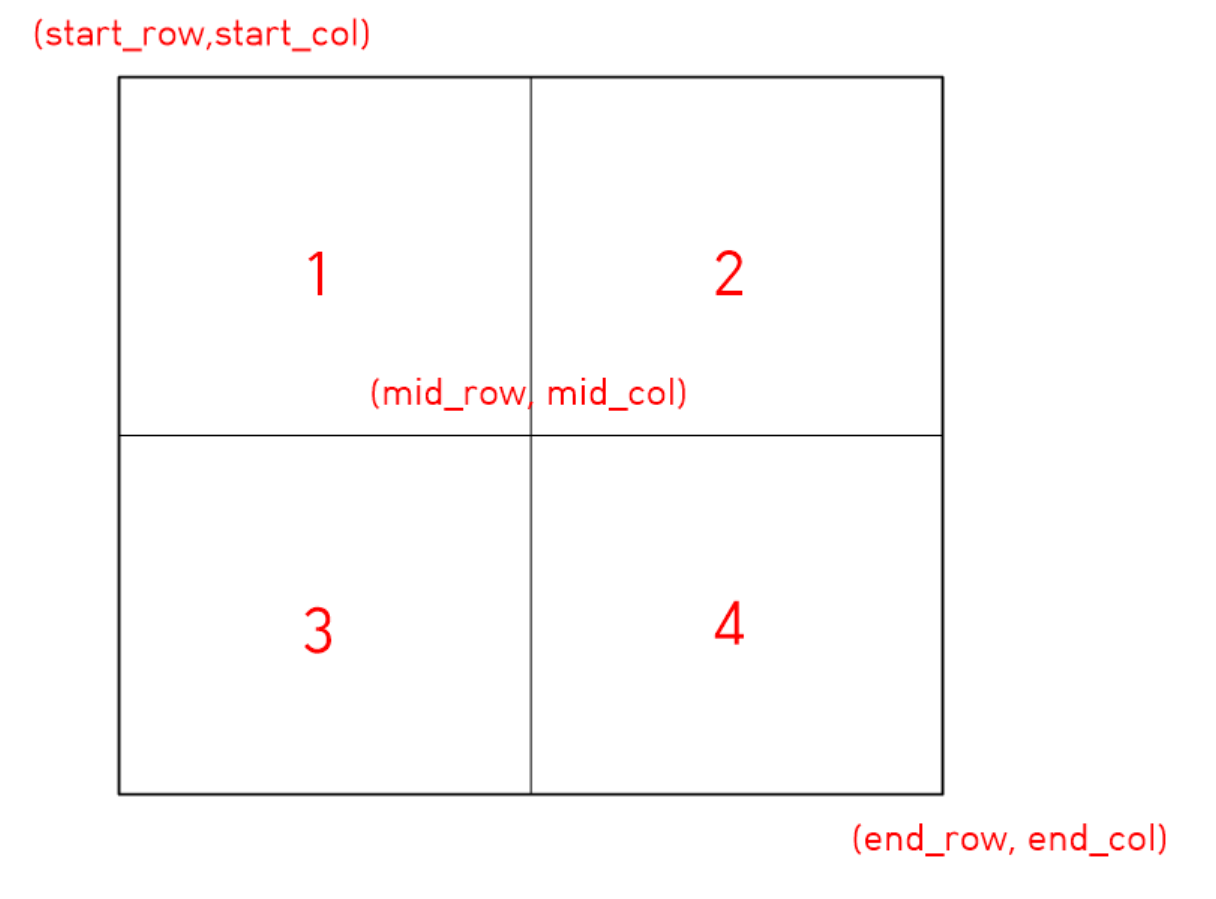
분할 정복으로 풀기 위해서 mid_row, mid_col을 알아야 했다.

mid_row와 mid_col을 어떻게 구하지?🤔

mid_row, mid_col = (start_row + end_row) // 2, (start_col + end_col) // 2

순서는 1, 2, 3, 4 순으로 어떻게 구현할까?🤔

direction = [
            (start_row, start_col, mid_row, mid_col), => 1사분면
            (start_row, mid_col, mid_row, end_col),	  => 2사분면
            (mid_row, start_col, end_row, mid_col),	  => 3사분면
            (mid_row,mid_col, end_row, end_col)		  => 4사분면
        ]

전체코드

for test_case in range(1):
    n, r, c = map(int, sys.stdin.readline().split())

    cnt = 0
    graph = []
    for row in range(2**n):
        tmp = []
        for col in range(2**n):
            tmp.append(cnt)
            cnt += 1
        graph.append(tmp)
    ans = 0
    def dfs(depth, start_row, start_col, end_row, end_col):
        global ans
        if depth == 0:
            if start_row == r and start_col == c:
                print(ans)
            ans += 1
            return

        mid_row, mid_col = (start_row + end_row) // 2, (start_col + end_col) // 2
        direction = [
            (start_row, start_col, mid_row, mid_col),
            (start_row, mid_col, mid_row, end_col),
            (mid_row, start_col, end_row, mid_col),
            (mid_row,mid_col, end_row, end_col)
        ]

        for new_start_row, new_start_col, new_end_row, new_end_col in direction:
            dfs(depth-1,new_start_row, new_start_col, new_end_row, new_end_col )


    dfs(n, 0, 0, 2**n, 2**n)

TLE 발생한다. ㅠㅠ
이유는 2^15 * 2^15은 상당히 큰 숫자이다. 이렇게 모든 경로를 탐색하면 안된다.

📝 아이디어

모든 경로를 탐색하지 않고 4사분면 기준으로 어디에 위치하는지 알면된다.

예를 들어 3사분면에 있다고 생각해보자
1, 2사분면을 탐색할 이유가 없다. 1, 2사분면 전체 길이를 더해주고 3사분면에서 재귀적으로 구하면 된다.

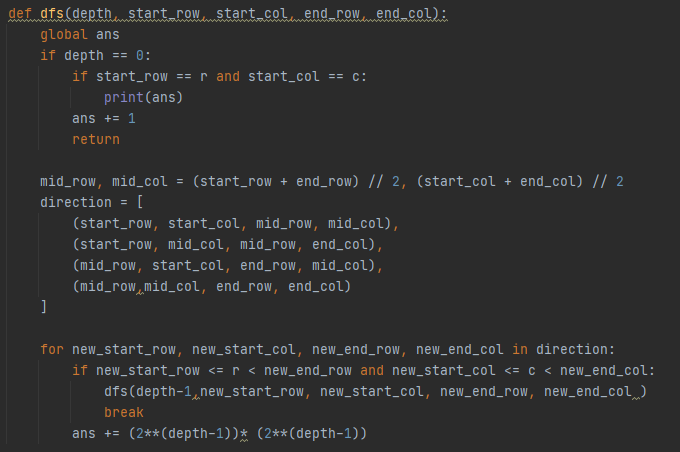
일단 순서(1,2,3,4 사분면 순서)를 나타내는 배열 direction을 구한다.
여기서 찾고자 하는 위치 r, c가 해당 사분면에 있다면 그 사분면을 탐색한다.
또한 이전 사분면의 길이를 더해주면 된다.