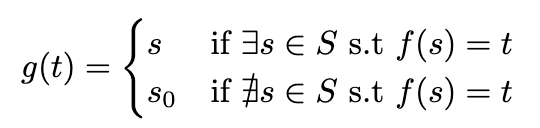칸토어 이론 증명

하기 싫은 공부를 더 이상 미룰 수 없다.
과연 컴퓨터로 임의의 숫자를 표현하는게 가능한지 증명을 해보자.
요즘 메타버스 어쩌구 하던데, 과연 컴퓨터는 현실세계의 데이터를 담아내는 것이 이론적으로 가능한 것인가?
결론: 컴퓨터의 메모리가 무한히 크고, CPU 연산량이 무한히 빠르면 가능하다
하지만 당연하게도 현실적으로 불가능하다.

Reference 링크 에 적힌 책을 읽고 요약 정리해보았다.

Definition 1.1 (one-to-one)

function $f:S \rightarrow T$ is injective if
$\forall x,x' \in S$, $x \neq x' \Rightarrow f(x) \neq f(x')$

Lemma 1.2

$S,T \neq \emptyset$ and $f:S \rightarrow T$ is one to one.
Then, $\exists$ onto function $g:T \rightarrow S$ s.t $g(f(s)) = s$ for $\forall s \in S$
Proof
Choose some $s_0 \in S$ and define $g:T \rightarrow S$ as follows.

Since $f$ is one-to-one, $\forall s,s' \in S, s \neq s' \Rightarrow f(s) \neq f(s')$.
Let $t=f(s), t'=f(s')$. Then, $t=t' \Rightarrow g(t)=g(t')$.
$\therefore$ $g$ is a function.

Since $f$ is a function, $\forall s \in S, \exists t \in T$ s.t $f(s)=t$.
$\Rightarrow$ $\forall s \in S, \exists t \in T$ s.t $g(t)=g(f(s))=s$
$\therefore$ $g$ is onto.

Definition 2.7

$\{0,1\}^*$ = set of all finite sequences of bits = set of all bit strings
$\{0,1\}^\infty$ = set of all infinite sequences of bits
Let $f:\mathbb{N} \rightarrow \{0,1\}$
Then, $(f(0),f(1),f(2),\dots)$ is an infinite sequence of bits
$\Rightarrow f$ is an infinite sequence of bits
$\therefore \{0,1\}^\infty = \{f|f:\mathbb{N} \rightarrow \{0,1\}\}$

Lemma 2.8

$\nexists$ one-to-one map $FtS: \{0,1\}^\infty \rightarrow \{0,1\}^*$
proof
$\nexists$ one-to-one map $FtS: \{0,1\}^\infty \rightarrow \{0,1\}^*$
$\Leftrightarrow \nexists$ onto function $StF:\{0,1\}^* \rightarrow \{0,1\}^\infty$

Suppose $\exists$ onto function $StF: \{0,1\}^* \rightarrow \{0,1\}^\infty$
$\Rightarrow \forall \overline{d} \in \{0,1\}^\infty, \exists x \in \{0,1\}^*$ s.t $StF(x) = \overline{d}$

Define $\overline{d} \in \{0,1\}^\infty$ as follows.

Where $n \in \mathbb{N}$, $x_n \in \{0,1\}^*$, and
$StF(x_n)(n) \in \{0,1\}$ is the n-th bit of $StF(x_n) \in \{0,1\}^\infty$.

Since $\overline{d}$ is a "diagonal argument", $\nexists x \in \{0,1\}^*$ s.t $StF(x) = \overline{d}$
$\therefore$ Proved by contradiction.

Lemma 2.9

$\exists$ one-to-one map $FtR: \{0,1\}^\infty \rightarrow \mathbb{R}$
proof
For $f \in \{0,1\}^\infty$, Define $FtR$ as follows.

Then, $FtR(f) \in \mathbb{R}$ and $FtR$ is one-to-one.

Theorem 2.5 (Cantor's Theorem)

The reals are uncountable.
proof
The reals are uncountable.
$\Leftrightarrow \nexists$ onto function $NtR: \mathbb{N} \rightarrow \mathbb{R}$
$\Leftrightarrow \nexists$ one-to-one function $RtS: \mathbb{R} \rightarrow \{0,1\}^*$

Suppose there exists one-to-one function RtS.
From Lemma 2.9, $\exists$ one-to-one map $FtR: \{0,1\}^\infty \rightarrow \mathbb{R}$
Let $FtS = FtR \circ RtS$
Then, $FtS: \{0,1\}^\infty \rightarrow \{0,1\}^*$ is an one-to-one function.
However, $FtS$ can not be one-to-one from Lemma 2.8.
$\therefore$ Proved by contradiction.