Computing Every Function

지난 시간에 Computation 을 엄밀히 정의하면서,
computation 을 Circuit 으로 구현하든, 프로그램으로 구현하든,
그게 그거라는 것을 보였다.

또한 NAND 하나로, AND / OR / NOT 3가지를 다 표현 가능하니,
NAND 하나만으로 computation 을 구현할 수 있다.

이번 시간에는 NAND 하나만으로, 정말로 모든 함수를 compute 할 수 있는지 증명해보려 한다.

Definition (Lookup function)

$LOOKUP_k: \{0,1\}^{2^k+k}\rightarrow \{0,1\}$
Lookup function of order $k$ is defined as follows:
$x = x_0 x_1 \ldots x_{2^{k}-1} \in\{0,1\}^{2^k}$
$i = i_0 i_1 \ldots i_{k-1} \in \{0,1\}^k$

where $x_i$ = $i^{th}$ entry of $x$.

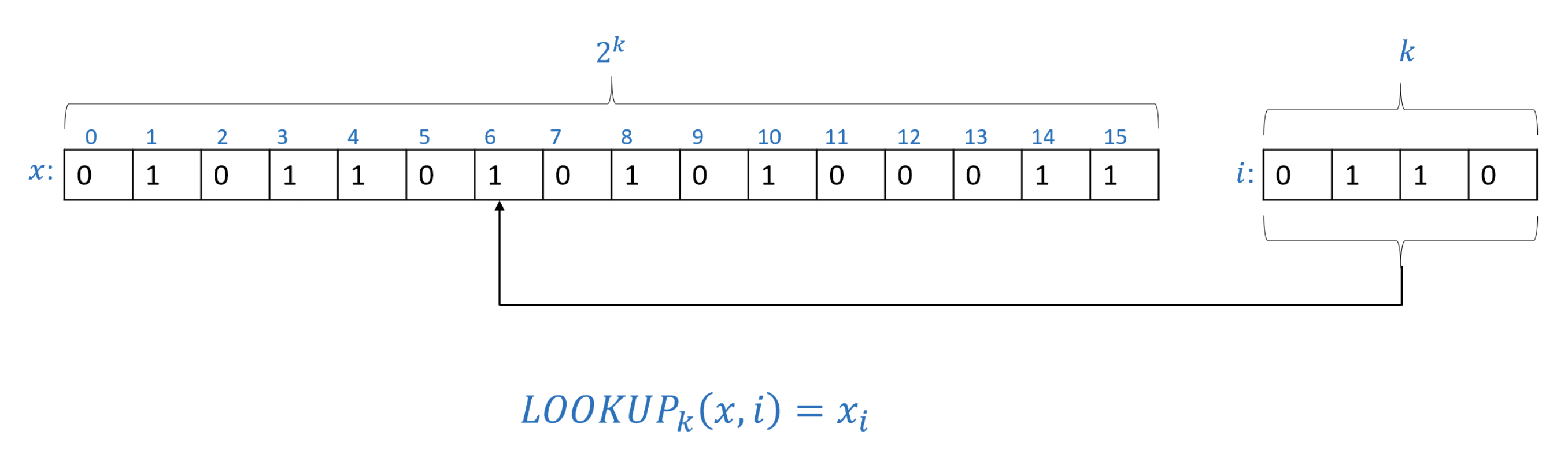
즉 Lookup function 이란, i bit string 을 숫자로 바꾸어서,
해당하는 숫자의 위치에 있는 i 번째 bit 를 x bit string 에서 가져오는 함수이다.

Lemma 4.11 (Lookup recursion)

$k \geq 2$
$a = LOOKUP_{k-1}(x_0,\ldots,x_{2^{k-1}-1},i_1,\ldots,i_{k-1})$
$b = LOOKUP_{k-1}(x_{2^{k-1}},\ldots,x_{2^k-1},i_1,\ldots,i_{k-1})$

Proof

If $i_{0} = 0$, then the index $i$ is in $\{0,\ldots,2^{k-1}-1\}$.
Perform the lookup on the first half of $x$.
Then, $LOOKUP_k(x,i) = LOOKUP_{k-1}(x_0,\ldots,x_{2^{k-1}-1},i_1,\ldots,i_{k-1}) = a$

If $i_{0} = 1$, then the index $i$ is in $\{2^{k-1},\ldots,2^k-1\}$.
Perform the lookup on the "second half" of $x$.
Then, $LOOKUP_k(x,i) = LOOKUP_{k-1}(x_{2^{k-1}},\ldots,x_{2^k-1},i_1,\ldots,i_{k-1}) = b$

증명이라기보다는 Lookup recursion 함수에 대한 설명 같다.

Theorem 4.10 (Lookup function 의 구현)

$LOOKUP_k: \{0,1\}^{2^k+k}\rightarrow \{0,1\}$ is a lookup function.
For $\forall k > 0$, $\exists$ NAND-CIRC program that computes $LOOKUP_k$.
Moreover, the number of lines in this program $\leq 4 \cdot 2^k$

Proof

For $k = 1$,
$LOOKUP_1: \{0,1\}^{3}\rightarrow \{0,1\}$ can be computed by
4 line NAND-CIRC program.

def IF(cond,a,b):
  notcond = NAND(cond,cond)
  temp = NAND(b,notcond)
  temp1 = NAND(a,cond)
  return NAND(temp,temp1)

For $k \geq 2$,
We can apply Lemma 4.11.
$a = LOOKUP_{k-1}(x_0,\ldots,x_{2^{k-1}-1},i_1,\ldots,i_{k-1})$ \
$b = LOOKUP_{k-1}(x_{2^{k-1}},\ldots,x_{2^k-1},i_1,\ldots,i_{k-1})$

Recursively call $LOOKUP_k$ until $k$ becomes 1.
Then, we have $4 \cdot 2^k$ lines of NAND-CIRC program.

Theorem 4.12 (Universality of NAND)

For $n,m>0$ and function $f: \{0,1\}^n\rightarrow \{0,1\}^m$
$\exists$ constant $c>0$ such that
$\exists$ Boolean circuit with at most $c \cdot m 2^n$ gates that computes the function $f$.

Proof

For $\forall$ function $f: \{0,1\}^n \rightarrow \{0,1\}$,
we can write a NAND-CIRC program that does the following:

1. Initialize $2^n$ variables of the form
   temp = NAND(X[0], X[1])
   one = NAND(X[0], temp)
   zero = NAND(one, one)
   $x_0 = f(00\cdots0)$, $\cdots$, $x_{2^n-1} = f(11\cdots1)$
   This requires $3 + 2^n$ lines of code.

2. Compute $LOOKUP_n$ on the $2^n$ variables initialized in the previous step,
   with the index variable $i = i_0 i_1 \dots i_{n-1}$ being the input variables.
   $LOOKUP_n(x_0,\dots,x_{2^n-1},i_0,\cdots,i_{n-1})$
   This requires at most $4\cdot 2^n$ lines of code by Theorem 4.10.

$y = y_0 \dots y_{m-1} \in \{0,1\}^m$
$l \in [m] = \{0, 1, \dots, m-1\}$
total number of lines for computing one bit $y_l \in \{0,1\}$
$\leq (3+2^n) + (4\cdot 2^n) = 3 + 5 \cdot 2^n$

Repeat the computation of one bit $y_l \in \{0,1\}$ for m times.
Then, we can get $y = y_0 \dots y_{m-1} \in \{0,1\}^m$

$\therefore$ the total number of lines for computing function $\leq m \cdot (3 + 5 \cdot 2^n)$

This completes the proof.