택배 배달과 수거하기 150369

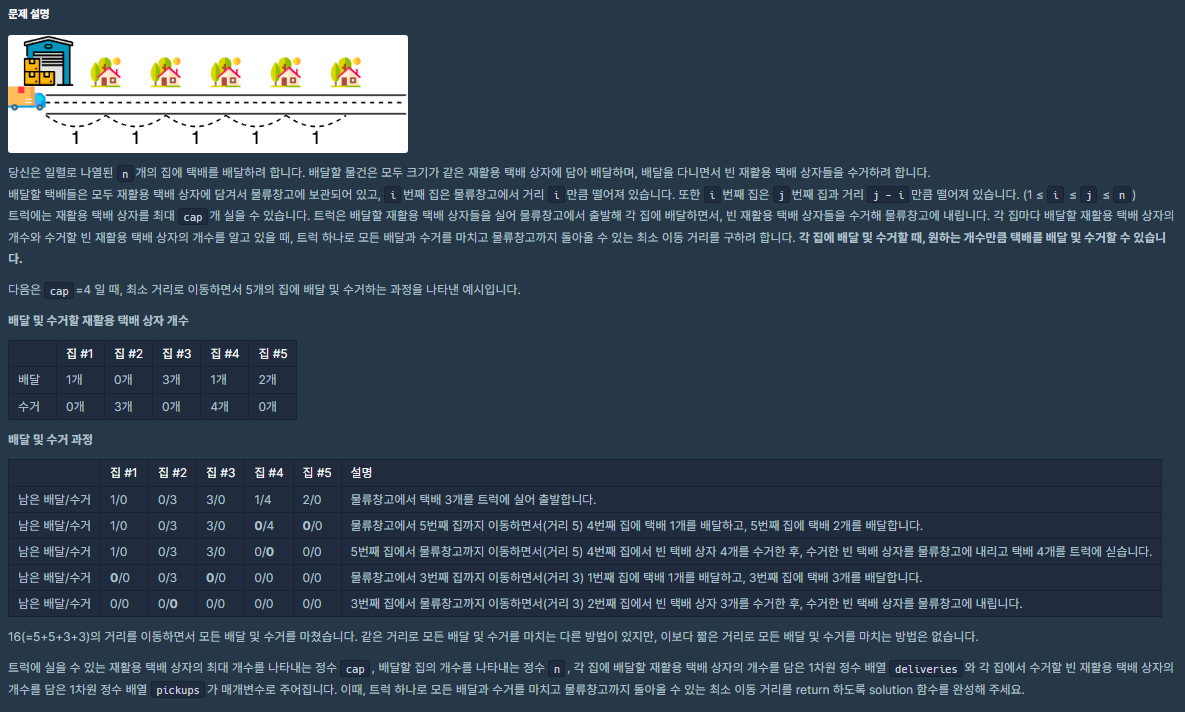
문제

접근 방법

수거와 배달의 원리를 살펴보자.

1. 가장 먼 곳을 간다.
2. 차례대로 배달 (오는 동안) 또는 수거(가는 동안)를 한다.
3. 다시 돌아온다.
4. 모든 곳이 배달 또는 수거될 때까지 1번으로 돌아간다.

중복되는 부분이 많다.
수거, 배달 모두 먼 곳에서부터 해결해주면 최소 이동 거리를 보장한다.
배달 후 수거를 한다고 생각하면 중복되는 거리 또한 해결해준다.
즉 두 부분의 가장 먼 거리를 구한 뒤 2배를 한 값을 합산하면 된다.

코드

#include <string>
#include <vector>
using namespace std;
pair<int, int> getLenIdx(vector<int> &v, int cap, int _idx)
{
    int idx = _idx, len = 0;
    while (idx >= 0 && !v[idx])
    {
        --idx;
    }
    if (idx < 0)
        return {-1, 0};
    else
    {
        len = idx + 1;
    }
    while (idx >= 0 && cap)
    {
        if (v[idx] <= cap)
        {
            cap -= v[idx];
            v[idx] = 0;
            --idx;
        }
        else
        {
            v[idx] -= cap;
            cap = 0;
        }
    }
    return {idx, len};
}
long long solution(int cap, int n, vector<int> deliveries, vector<int> pickups)
{
    long long answer = 0;
    int deliIdx = n - 1, pickIdx = n - 1;
    while (deliIdx >= 0 || pickIdx >= 0)
    {
        auto deli = getLenIdx(deliveries, cap, deliIdx);
        deliIdx = deli.first;
        auto pick = getLenIdx(pickups, cap, pickIdx);
        pickIdx = pick.first;
        answer += (deli.second > pick.second ? deli.second : pick.second) << 1;
    }
    return answer;
}

풀이

인덱스와 거리는 1만큼 차이 있다는 것을 명심하면 좋다.
배달이나 수거가 비어있을 수도 있다는 점 또한 명심하면 좋다.
가장 먼 곳부터 해결하기에 그리디라고 생각한다.