카드 구매하기 11052

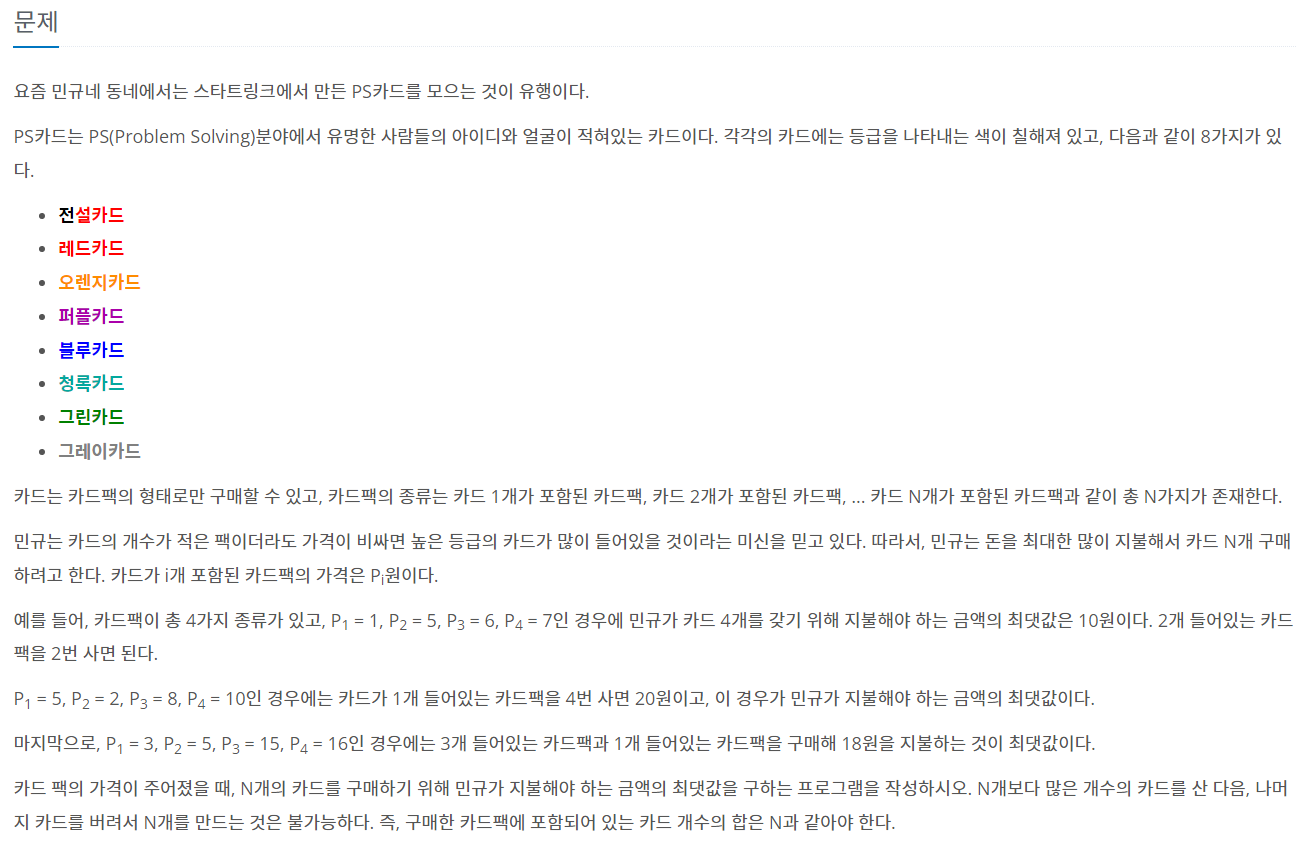
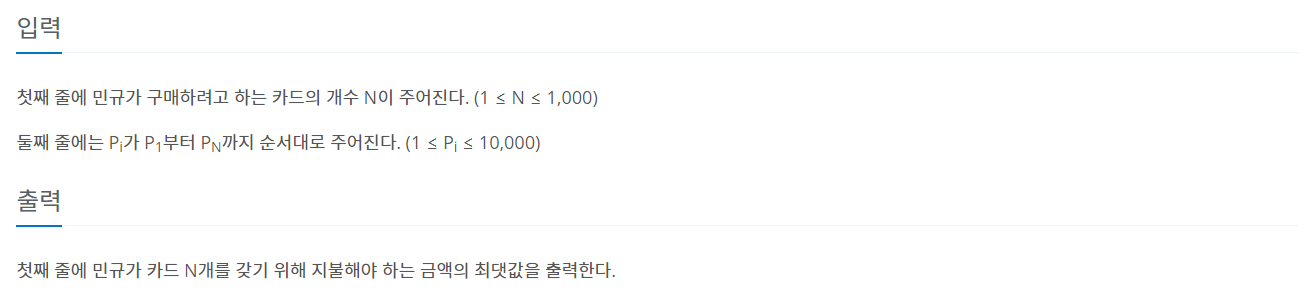
문제

접근 방법

1개일 경우
1
2개일 경우
1+1, 2
3개일 경우
1+1+1, 2+1, 3
1+2
4개일 경우
1+1+1+1, 2+1+1, 2+2, 3+1, 4
1+2+1, 1+3
겹치는 부분이 보인다. 우리에게 중요한 것은 N개를 사용했을 경우에 최댓값이다. 즉 이렇게 바꿀 수 있을 것이다.

1개일 경우
1
2개일 경우
1개일 경우+1, 2
3개일 경우
2개일 경우+1, 3
4개일 경우
3개일 경우+1, 2개일 경우+2개일 경우, 4

이것을 예제 입력 1에 적용해서 확인해본다.
1개일 경우 1
2개일 경우 1+1, 5
3개일 경우 5+1, 6
4개일 경우 6+1, 5+5, 7

예제 입력 2에도 적용해본다.
1개일 경우 10
2개일 경우 10+10, 9
3개일 경우 10+10+10, 8
4개일 경우 10+10+10+10, 10+10+10+10, 7
5개일 경우 10+10+10+10+10, 10+10+10+10+10, 6

6개일 경우를 생각해보겠다.
6개일 경우, 5개일 경우+1개일 경우, 4개일 경우+ 2개일 경우, 3개일 경우+3개일 경우 이렇게 나뉠 것이다.
즉 N개의 경우는 N부터 (N+1)/2개의 경우까지 확인하면 된다.

코드

#include <iostream>
#include <vector>
using namespace std;
int main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int N;
    cin >> N;
    vector<int> prices(N + 1), dp(N + 1);
    for (int i = 1; i <= N; ++i)
        cin >> prices[i];
    for (int i = 1; i <= N; ++i)
    {
        dp[i] = prices[i];
        for (int j = (i + 1) / 2; j < i; ++j)
        {
            int price = dp[j] + prices[i - j];
            dp[i] = price > dp[i] ? price : dp[i];
        }
    }
    cout << dp[N];
    return 0;
}

풀이

DP는 규칙을 찾아내어서 해결하면 된다.
가장 작은 부분에서 시작하여 큰 부분으로 나아가면 된다.
겹치는 부분을 해소해줄 방법이 무엇인지 생각해보면 풀 수 있을 것이다.