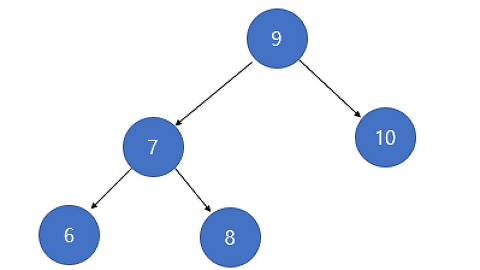
트리 용어
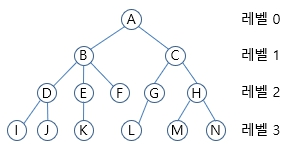
노드- 트리를 구성하는 기본원소
- ex) A, B, C...관계(가지)- 노드와 노드간의 연결선차수- 한 노드에 연결된 자식 노드의 수
- ex) A차수: 2, B차수: 3...계수- 자식 노드들 중 최대 개수
- ex) B의 자식: 3 => 계수=3레벨- 루트로부터의 단순 경로의 길이
- ex) A 레벨: 0, B, C의 레벨: 1높이- 최대 레벨 + 1
- ex) 최대 높이: 4경로- 한 노드에서 다른 한 노드에 이르는 경로 사이에 놓여있는 노드들의 순서경로 길이- 출발 노드에서 목적 노드까지 거치는 노드의 개수root node- 부모가 없는 최상위 노드
- ex) Aleaf node- 최하단 노드
- ex) F, I, J, K, L...단말 노드- 가지를 가지지 않는 차수가 0인 노드부모 노드- ex) D, E, F의 부모노드는 B자식 노드- ex) B의 자식노드는 D, E, F형제 노드- ex) D, E, F 는 동일한 부모를 갖는 형제노드크기- 특정 노드가 자신을 포함한 자손의 수서브트리- ex) B를 루트로 하는 트리를 A의 왼쪽 서브트리,
C를 루트로 하는 트리를 A의 오른쪽 서브트리라 지칭
이진트리
- 각각의 노드가 최대 두개의 자식 노드를 가지는 트리 자료 구조
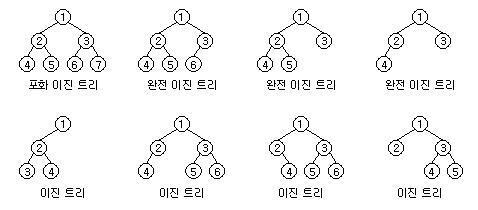
이진트리의 종류
정이진트리
- 트리의 모든 node가 0개 혹은 2개의 자식을 가지는 경우
포화이진트리
- leaf node가 끝까지 정말 꽉 찬 트리를 의미
완전이진트리
- 마지막 레벨을 제외한 모든 레벨에서 순서대로 node가 꽉 채워진 트리를 의미
균형이진트리
- leaf node들의 레벨차이가 최대 1레벨까지만 나는 트리
- 트리의 높이를 균형적으로 유지 (B트리에서 주로 사용)
B트리
B-트리
- 이진트리와는 다르게 하나의 노드에 많은 정보를 가질 수 있음
- 이렇게 정보를 담게 되면서
차수라는 개념이 생김
- 이렇게 정보를 담게 되면서
- 많은 데이터베이스들이 B-Tree를 채용함
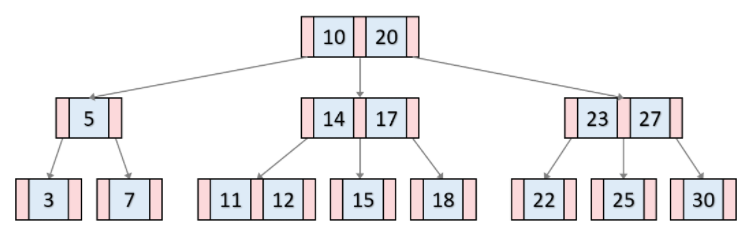
- 균형이진트리의 연속
- 균형을 계속 유지 (최악의 경우에도
O(logN)유지)
- 균형을 계속 유지 (최악의 경우에도
B-트리 탐색 과정
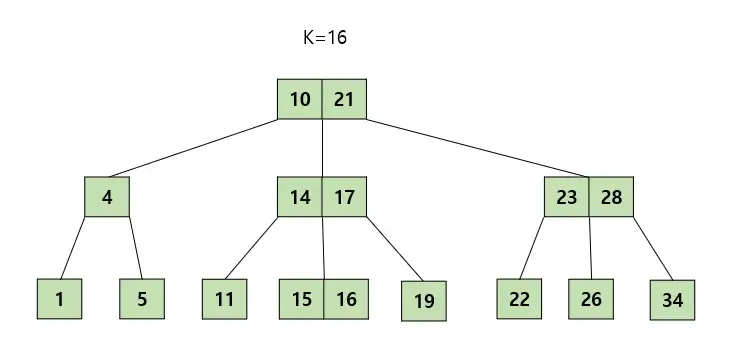
1) 루트 노드에서 탐색을 시작
3) k와 노드의 key값을 비교해 알맞은 자식노드로 이동
4) 해당 과정을 leaf node에 도달할 때 까지 반복
5) leaf node에서도 k를 찾지 못한다면 트리에 값 존재 X
B-트리의 특징
- 각 노드의 자료는 정렬되어있음
- 자료 중복 X
- 모든
leaf node는 같은 레벨에 존재 root node는 자신이leaf node가 되지 않는 이상 적어도 2개 이상의 자식을 보유root node가 아닌 노드들은 적어도 M/2 개의 자식을 보유(최대: M개)
B*트리
- B-트리의 구조를 유지하기 위한 추가적연산이나 새로운 노드 생성의 최소화를 위해 B-트리에서 몇가지 규칙이 추가된 구조
- 기존 노드의 자식 노드 수 최소 제약 조건
2M/3개 - 노드가 가득 찰 시, 분열 대신 이웃 형제노드로 재배치
B*트리의 특징
- 각 노드 자료는 정렬되어있음
- 자료 중복 X
- 모든
leaf node는 같은 레벨에 있음 root node는 자신이leaf node가 되지않는이상 적어도 2개 이상의 자식을 보유root node가 아닌 노드들은 적어도 2[(M-2)/3]+1개의 자식 노드를 보유 (최대 M개)
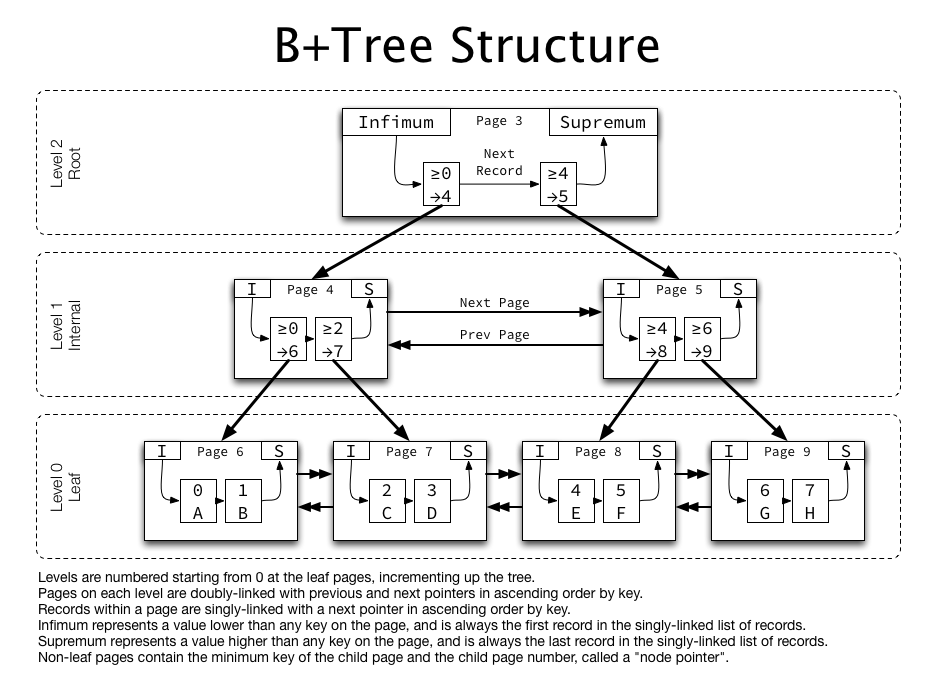
B+ 트리
- B-트리의 탐색을 위한 노드를 찾아서 이동해야하는 단점을 해소한 구조
- 같은 레벨의 모든 키값들이 정렬
- 같은 레벨의
Sibiling node는 연결리스트 형태- 모두 연결되어있어 키값 중복 X
- 탐색 시
leaf node에 모든 자료가 존재하고 그 자료들이연결리스트로 연결되어있어 탐색에 있어 유리
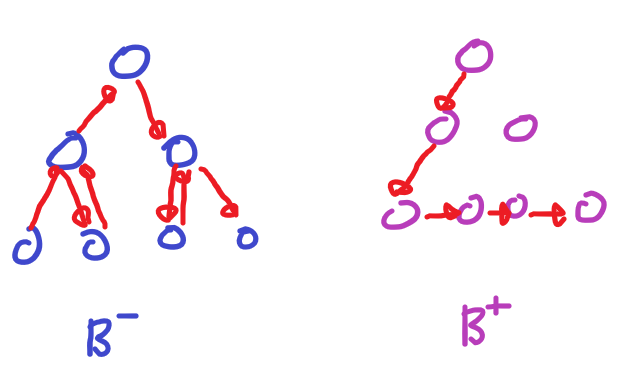
- leaf node는
데이터 노드, 아닌 자료는인덱스 노드
인덱스노드
- Value 값에는 다음 노드를 가리킬 수 있는 포인터 주소 존재
데이터노드
- Value 값에 데이터가 존재
특징
- 데이터 노드의 자료는 정렬되어있음
- 데이터 노드 중복 X
- 모든
leaf node는 같은 레벨에 존재 leaf node가 아닌node의 키 값의 수는 그 노드의 서브트리수보다 하나가 적음- 모든
leaf node는 연결리스트로 연결되어있음 - 키값의 중복 O (인덱스 노드와 데이터 노드에서 동시 등장 가능)
- 데이터 검색을 위해 반드시
leaf node까지 내려가야 함 - 대부분의 데이터베이스 시스템은
B+Tree구조를 채택