Neural Network - MLP (Multi-Layer Perceptron)

Neural Networks

• 신경망은 비선형 변환에 이어 기하학적 변화를 쌓는 function approximators
  

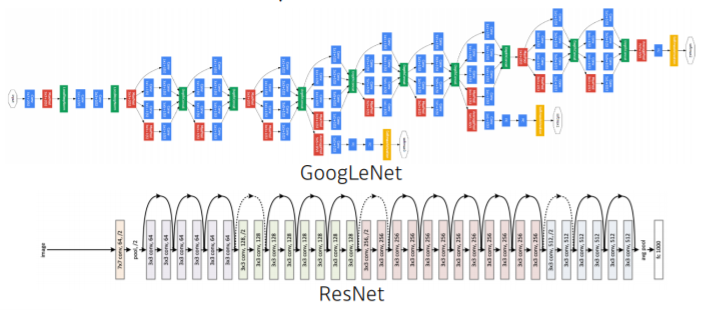
Linear Neural Networks

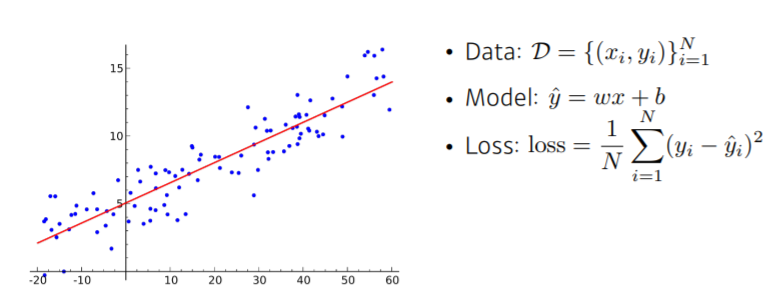
• model에서의 기울기 w와 y절편 b를 찾는 것이 목표
• loss는 이루고자 하는 쪽에 가까워질수록 값이 작아지게 됨 (MSE)
  
• 위의 식 수행함으로써 내 parameter가 어느 방향으로 움직였을 때 loss function이 감소하는가 확인 가능
  
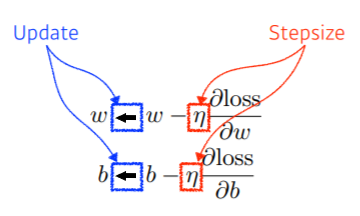
• 계속해서 위와 같이 update하는 것을 gradient descent
  
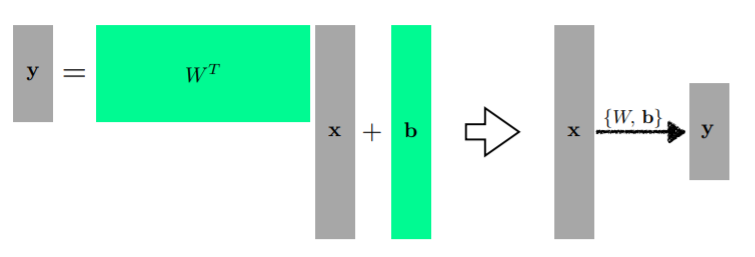
• 위 그림과 같이 다차원 input과 output도 다룰 수 있음

Beyond Linear Neural Networks

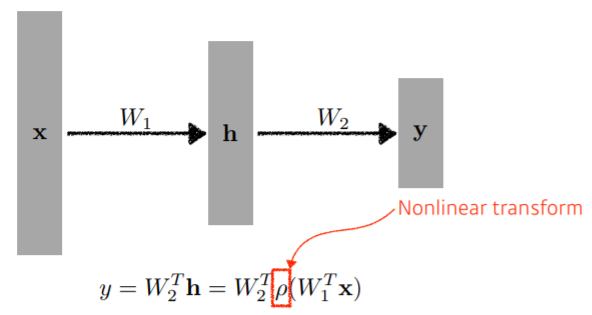
• Matrix 형태인 W로 두 개의 vector space간의 선형 변환 지원
• h는 hidden layer
• 학습률 ρ를 이용하여 x에서 y의 mapping 표현력 최대화
• hidden layer가 하나 있는 neural network는 대부분의 continuous map과 measurable function을 근사할 수 있음
  - hidden layer가 대부분의 continuous function들을 다 포함하기 때문
  

Activation Functions

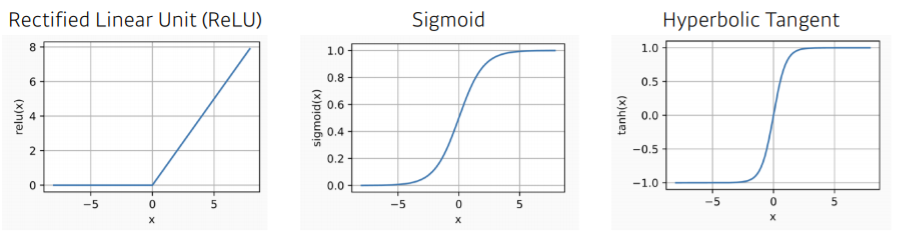
• 대표적인 활성화함수 3개 (ReLU, sigmoid, Hyperbolic Tangent)
• network 깊게 쌓았을 때 활성화 함수 사용하면 좋음

Multi-Layer Perceptron

• 최종 output까지의 과정 중 hidden layer가 있는 것을 Multi-Layer Perceptron
• 3차원 MLP
  
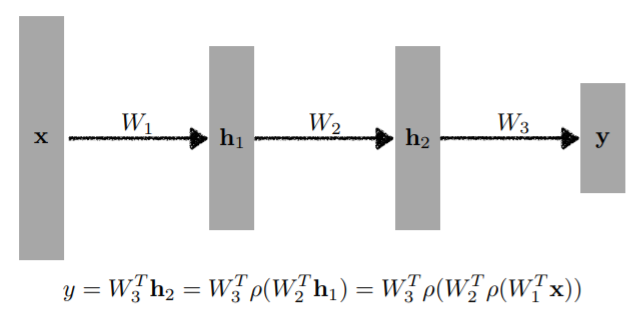
  - input → fine transformation → hidden layer → fine transformation → hidden layer → fine transformation → output

Loss Functions

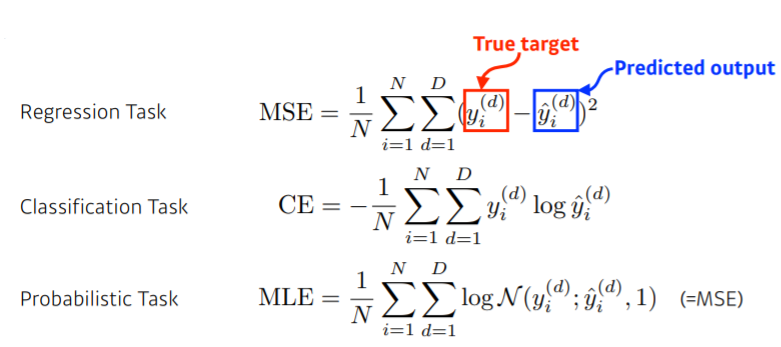
• Regression Task에선 MSE 사용. 그러나 local minimum으로 구할 가능성 있음
• Classification Task에선 주로 CE 사용. 그 차원에 해당하는 값을 늘림
• Probabilistic Task, uncertainty를 분류하기 위한 task에선 MLE(=MSE) 사용