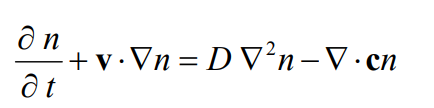Transport of Nanoparticles in Gases:Overview and Recent Advances(Lutz Madler, 2007)
Transport Phenomena(Bird, Stewart, and Lighfoot,2002)

Brownian Diffusion

Particle Diffusivity

Fick's Diffusion Equation

Fick's second Law

${\partial n \over \partial t}=D{\partial^2n\over\partial x^2}$

$n$ = the one-dimensional (x-coordinate) particle number concentration
$n_0$ at $t=0$

사고 실험을 하나 해봅시다.

x축으로만 갈 수 있는 공간에서 monodisperse cloud of Particles를 짧은 주기로 방출할거에요
Dirac's delta function을 따르도록 할게요!
Ficks의 확산방정식을 생각하면 BCs는 아래와 같습니다

$t=0, n=n_0\delta(x)$
$t>0, x=\infin, n=0$
$t>0, x=0, \partial n /\partial x = 0$

그럼 확산 방정식의 solution은 Gaussian Curve를 따릅니다.

$n(x,t) = {n_0\over 2\sqrt{\pi Dt}}exp(-{x^2\over 4Dt})$

그럼 particle의 평균 거리($\bar{x}$)는 0 이겠네요

정리하면, the mean square displacement는 1차원에서 아래와 같겠죠?

$\bar{x^2}=2Dt$

이게 Einstein Equation을 의미한다고 하네요?
그러니까 확산하는 Particle의 평균 제곱 거리는 Particle의 Diffusivity와 Time에 비례한다.

Force Balance

BSL의 책에서 발췌한 Force Balance 식은 아래와 같다

$m{du\over dt}=-F_D +F(t)=-\zeta u+F(t)$

$m$ = the mass of particle
$u$ = particles velocity
$F_D$ = the drag force
$F(t)$ = a fluctuating force
$\zeta$ = the friction coefficient

여기서 Fluctuating Force 는 주변의 fluid 분자들과 particle의 충돌에 의한 것이다.
(because the fluid molecules are in thermal motion)

그리고 $\zeta$는 particle velocity와는 독립이고,
particle size/shaep/fluid properties에 의존한다고 가정한다

식을 만져보자

$m{du\over dt}=-F_D +F(t)=-\zeta u+F(t)$

→ $x{du\over dt}+\beta ux = x A(t)$ $where\;\beta = \zeta/m, A(t) = F(t)/m$

→ ${d(ux) \over dt}+\beta (ux) = u^2+A(t)x$

→ $u(x) = exp(-\beta t)\int_0^tu^2exp(\beta t' )dt'+exp(-\beta t)\int_0^tA(t)exp(\beta t' )dt'$

그럼 뭐 뭐 그 이후에도 많은 과정을 거치는데,
지금 너무 졸리니까
중간에 들어간 가정만 적으면

$A(t)$는 $x$랑 상관이 없고(당연함)
time $t$가 the relaxation time of particles에 비해 훨씬 크다면

$t>>1/\beta$

그리고 particle의 velocity에 대해
kinetic energy에서 translational energy of a gas molecules만 생각 했을 때,

The Einstein relation

$D={kT\over \zeta}$

로 표현될수 있다.

Continuum and free molecular approaches

mean free path

the gas mean free path(Willeke,1976);

$l_{gas}=l_{gas,0} \left({T\over T_0}\right)\left({p_0\over p}\right)\left({1+{S\over T_0}\over 1+{S\over T}}\right)$
where $S$ = the Sutherland constant

Particle Friction Coefficient $\zeta$

In the Stokes regime (Re≪1) & Continuum Regime (Kn≪1)

In Stokes Regime, Stokes' Law에 따라서 Friction Coefficient는 아래와 같이 표현할 수 있음 (particle은 spherical hard particle이라는 가정도 포함)

$\zeta = 3\pi\mu_B d_P$

근데 해당 식을 전개할 때, Stokes는 Particle 벽에서 상대속도가 0이라는 가정을 하는데, 해당 가정은 Continuum Regime임을 의미함.
즉, Knudsen Number≪1이어야 하는데, 이는 Particle의 Diameter가 mfp대비 충분히 크다는 것을 의미

In Slip Regime

그럼 Particle이 mfp와 비교했을 때 크기가 비슷하다면?
벽에서 Fluid Molecules의 속도가 0이 아님.
즉, Slip이 일어날 것
이런 현상을 설명하기 위해 보정계수(the slip correction factor, Cunningham correction)가 사용됨

$\zeta = {3\pi\mu_B d_p\over C_c}$

$C_c=1+Kn\left(A_1 + A_2 exp[{-2A_3\over Kn}]\right)$

where $A_1 = 1.257,\; A_2 =0.40, \;A_3 = 0.55$ (Davies,1945)

In free molecular regime (Kn≫1)

아래 식에서는 the accommodation coefficient (TMAC)가 포함되는데, 이 값은 입자가 벽에 충돌했을 때 난반사 되는 비율을 의미한다. 한 연구에서는 해당 값이 Knudsen Number와 관련이 있다고 보기도 한다(Li and Wang, 2003b)

$\zeta = {2\over 3}d_p^2\rho_B\sqrt{{2\pi \kappa T\over m_B}}\left(1+{\pi\alpha\over 8}\right)$

$\rho_B$ = the gas density
$m_B$ = the mass of gas molecule
$\alpha$ = the accommodation coefficient ~0.9 (general)

여기서 주목할 만한 차이점은, Stokes law에서는 the friction coefficient가 $d_p$에 비례했는데 the free molecular regime에서는 $d_p^2$에 비례한다는 점!

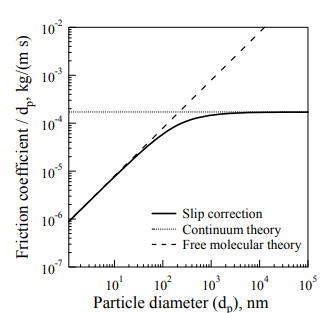
만약에 보고자 하는 particle이랑 gas molecules가 비슷한 사이즈 범위를 가지고 있다면, 즉, Kn = mfp/d_p 가 굉장히 크다면!
나아가 Kn→∞ 인 상황이라면?
(물론 Kn→∞ 일 수는 없다. ideal gas law 가정에 위배됨. 그래서 이 가정은 굉장히 조심스럽다)
Einstein Relation과 Chapman-Enskog equation은 equivalent 하다.

Start from Einstein Relation
① $D_{AB} = {\kappa T \over \zeta}$ - Einstein Relation

② $\zeta = {2\over 3}d_p^2\rho_B\sqrt{{2\pi \kappa T\over m_B}}\left(1+{\pi\alpha\over 8}\right)$ - the Friction Coefficient of the free molecular

③ $p=\rho_B RT$ - the ideal gas law

→ $D_{AB} = {1\over{2\over 3}\left(1+{\pi\alpha\over 8}\right)\sqrt{2\pi}}\sqrt{(RT)^3 \over M_B}{1\over d^2_PpN_A}$
where $M_B$ = 1mole당 가스 질량, $N_A$ = 아보가드로 수(${\kappa * N_A}= R$)

Chapman-Enskog Equation for mass diffusivity of binary mixture of nonpolar gases(low density):

$D_{AB} = {3\over16} \sqrt{{2(RT)^3\over\pi}({1\over M_A}+{1\over M_B})}{1\over N_A p \sigma^2_{AB} \Omega_{AB}}$

where $\Omega_{AB}$ = the collision integral
여기서 particle이 molecule보다는 충분히 크다고 생각하면 $M_A$>>$M_B$, $\sigma_A$>>$\sigma_B$, and set $\sigma_A = d_P$

두 식이 동일하다고 하면 우리가 얻을 수 있는 식은

$\Omega_{AB} = \left(1+{\pi\alpha\over 8}\right)$

Li and Wang(2003a)
Rudyak and Krasnolutski(2001)

Particle Mean Free Path

Temperature Gradient

Electric Forces

Convective Flows

Smoke, Dust, and Haze: Fundamentals of Aerosol Dynamics(Friendlander, 2000)
Particle를 이동시키는 3가지 메커니즘은 아래와 같다

• convection
• diffusion
• force fields
  ※ Particle Size와 Time이 주요 parameter가 되는 것도 잊지 말자