개념
- 다이나믹 프로그래밍을 활용한 대표적인 최단 경로(Shortest Path) 탐색 알고리즘
- 다익스트라 알고리즘은 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 확인
- 다익스트라 알고리즘이 다이나믹 프로그래밍 문제인 이유는 최단 거리는 여러 개의 최단 거리로 이루어져있기 때문
- 작은 문제가 큰 문제의 부분 집합에 속해있다고 볼 수 있음
- 따라서 기본적으로 다익스트라는 하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 특징
const arr = [
[0, 2, 5, 1, Infinity, Infinity],
[2, 0, 3, 2, Infinity, Infinity],
[5, 3, 0, 3, 1, 5],
[1, 2, 3, 0, 1, Infinity],
[Infinity, Infinity, 1, 1, 0, 2],
[Infinity, Infinity, 5, Infinity, 2, 0],
]
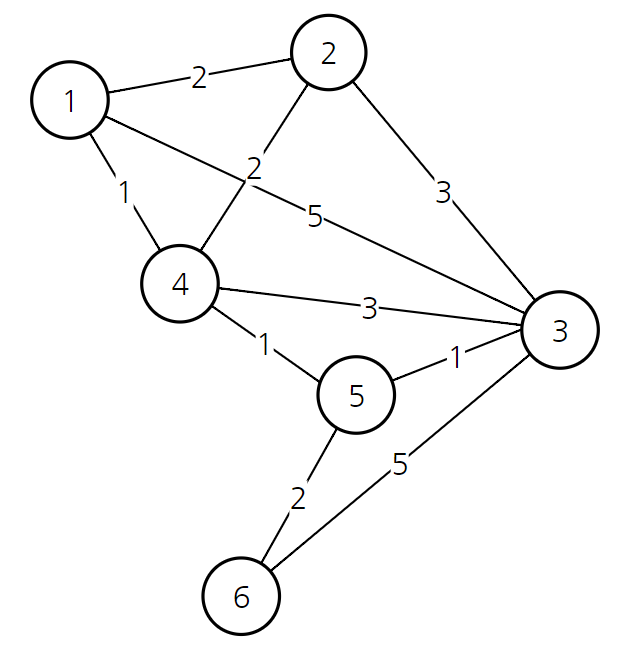
이미지 참고
구현(선형)
function solution(arr) {
const INF = Infinity;
const len = arr.length
const visit = new Array(len).fill(false)
const getMin = (vertex) => {
let min = INF;
let index = -1;
for (let i = 0; i < len; i++) {
if (!visit[i] && vertex[i] < min) {
min = vertex[i]
index = i
}
}
return index
}
const dijk = (start) => {
const record = arr[start].slice()
visit[start] = true
for (let i = 0; i < len; i++) {
const indexToGo = getMin(record)
if (indexToGo < 0) break
visit[indexToGo] = true
const currentVertex = arr[indexToGo]
for (let j = 0; j < len; j++) {
if (!visit[j] && record[j] > record[indexToGo] + currentVertex[j]) {
record[j] = record[indexToGo] + currentVertex[j]
}
}
}
return record
}
return dijk(0)
}
const arr = [
[0, 2, 5, 1, Infinity, Infinity],
[2, 0, 3, 2, Infinity, Infinity],
[5, 3, 0, 3, 1, 5],
[1, 2, 3, 0, 1, Infinity],
[Infinity, Infinity, 1, 1, 0, 2],
[Infinity, Infinity, 5, Infinity, 2, 0],
]
console.log(solution(arr));
설명 및 디버깅
function solution(arr) {
const INF = Infinity;
const len = arr.length
const visit = new Array(len).fill(false)
const getMin = (vertex) => {
let min = INF;
let index = -1;
for (let i = 0; i < len; i++) {
if (!visit[i] && vertex[i] < min) {
min = vertex[i]
index = i
}
}
console.log('=>', index);
return index
}
const dijk = (start) => {
const record = arr[start].slice()
visit[start] = true
for (let i = 0; i < len; i++) {
console.log("==========================================");
const indexToGo = getMin(record)
if (indexToGo < 0) break;
visit[indexToGo] = true
const currentVertex = arr[indexToGo]
for (let j = 0; j < len; j++) {
if (!visit[j] && record[j] > record[indexToGo] + currentVertex[j]) {
console.log("==========");
console.log("기존", record);
record[j] = record[indexToGo] + currentVertex[j]
console.log("갱신", record);
}
}
}
return record
}
return dijk(0)
}
const arr = [
[0, 2, 5, 1, Infinity, Infinity],
[2, 0, 3, 2, Infinity, Infinity],
[5, 3, 0, 3, 1, 5],
[1, 2, 3, 0, 1, Infinity],
[Infinity, Infinity, 1, 1, 0, 2],
[Infinity, Infinity, 5, Infinity, 2, 0],
]
console.log(solution(arr));
📚 참고
23. 다익스트라(Dijkstra) 알고리즘 by.안경잡이개발자


