알고리즘 13 해싱 | JS

해시테이블 | Hash Table

• dynamic set을 구현하는 효과적인 방법 중 하나
  적절한 가정하에서 평균 탐색, 삽입, 삭제시간 O(1)
  보통 최악의 경우 O(n!)

충돌 | colliision

• 두 개 이상의 키가 동일한 위치로 해싱되는 경우!
  즉, 서로 다른 두 키 k1과 k2에 대해서 h(k1) = h(k2)인 상황
• 일반적으로 |U|>>m이므로 항상 발생 가능(즉 단사함수가 아님)
• 만약 |K|>m이라면 당연히 발생, 여기서 K는 실제로저장된 키들의 집합
• 충돌이 발생할 경우 대처 방법이 필요
• 대표적인 두 가지 충돌 해결 방법: chaining & open addressing

충돌 해결: Chaining

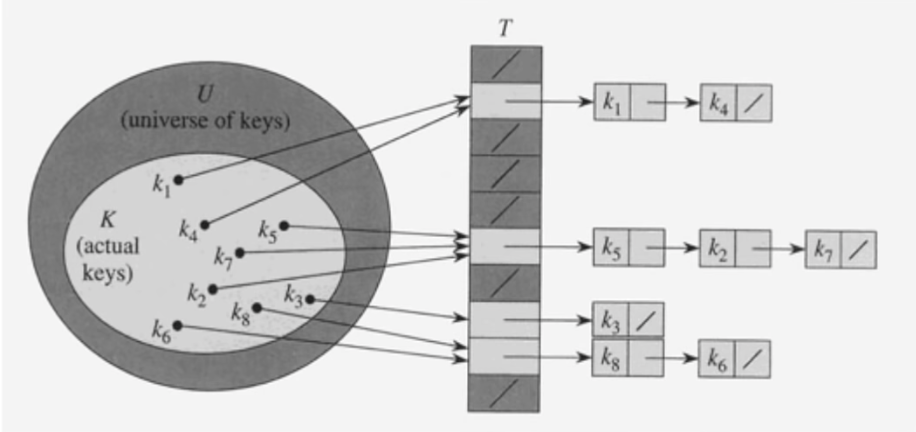
• 동일한 장소로 해싱된 모든 키들을 하나의 연결리스트(Linked List)로 저장
• 평균시간복잡도는 키들이 여러 슬롯에 얼마나 잘 분배되느냐에 의해서 결정

충돌 해결: Open Addressing

Linear probing

• 순차로 검색하여 빈 슬롯에 저장, 테이블의 끝에 도달하면 다시 처음으로 circular
• 클러스터가 계속해서 커지는 현상, 커지면 커질수록 키가 그 클러스터에 해당할 확률도 높아짐

Quadratic probing

• 충돌 발생 시, h(k), h(k)+1^2, h(k)+2^2, h(k)+3^2 ... 순서로 시도

Double hashing

• 서로 다른 두 해쉬 함수 h1과 h2를 이용
• h(k,i) = (h1(k) + i * h2(k))

Open Addressing에서 키의 삭제

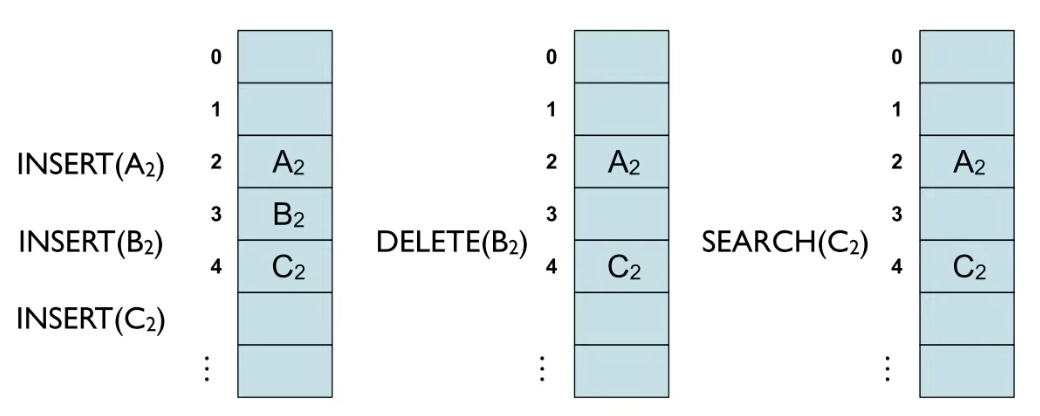
• 클러스터의 중간 값(B2)을 삭제할 경우 C2를 검색할 때 없는 값으로 오인할 수 있음
• 적당한 값을 비워진 중간 값으로 옮기는 작업이 필요

📚 참고

YOUTUBE | 2015 봄학기 알고리즘 | 권오흠

Photo by Michael Dziedzic on Unsplash