알고리즘 06 정렬 | 힙소트, 우선순위큐 | JS

protect-me·2021년 8월 30일

힙소트 힙정렬

📝 CS Study

목록 보기

23/37

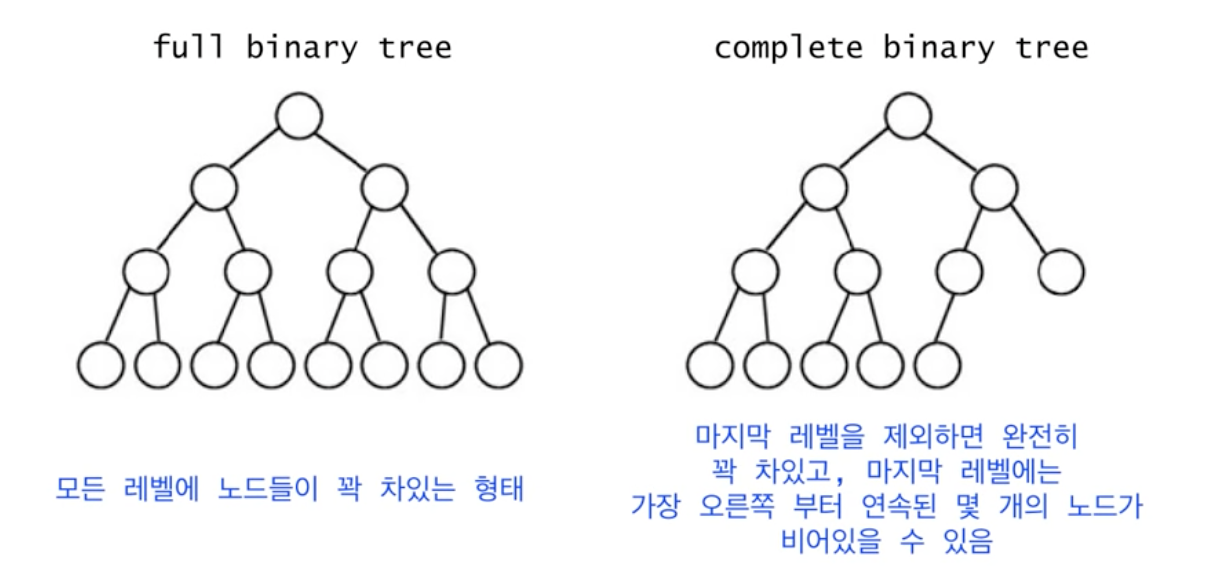
사전 지식: Full vs Complete Binary Tree

정 이진트리 | Full Binary Tree

완전 이진트리 | Complete Binary Tree

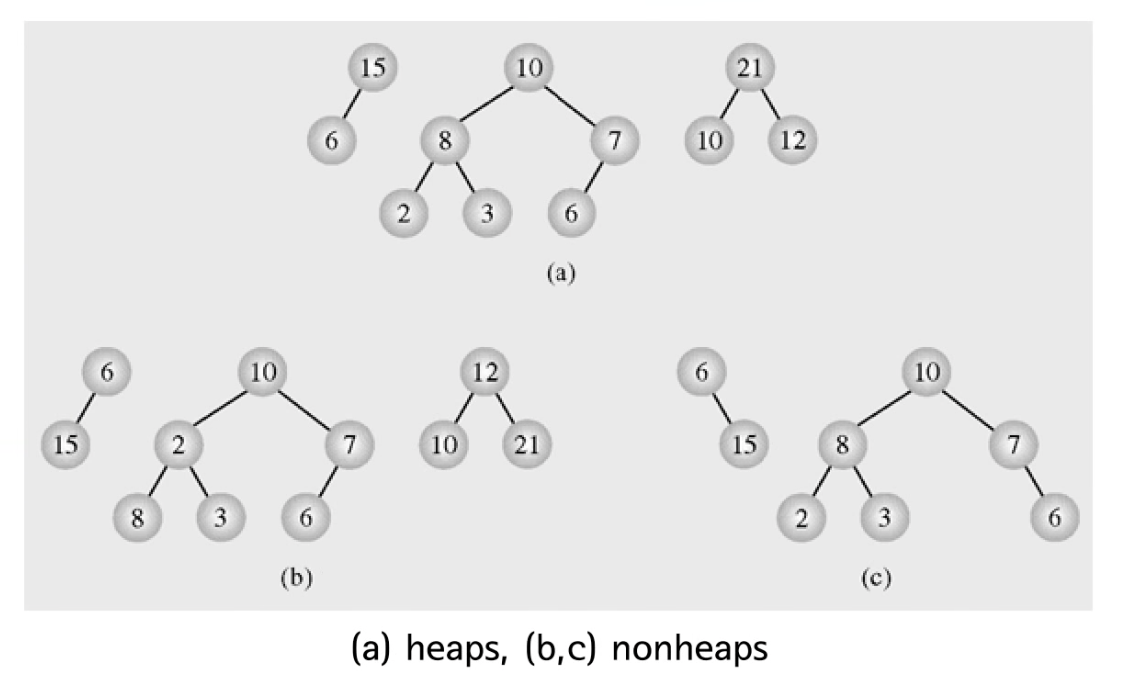
1. Heap이란?

complete binary tree이면서
heap property를 만족해야함(아래 이미지 참고)

Heap의 구분과 유일성

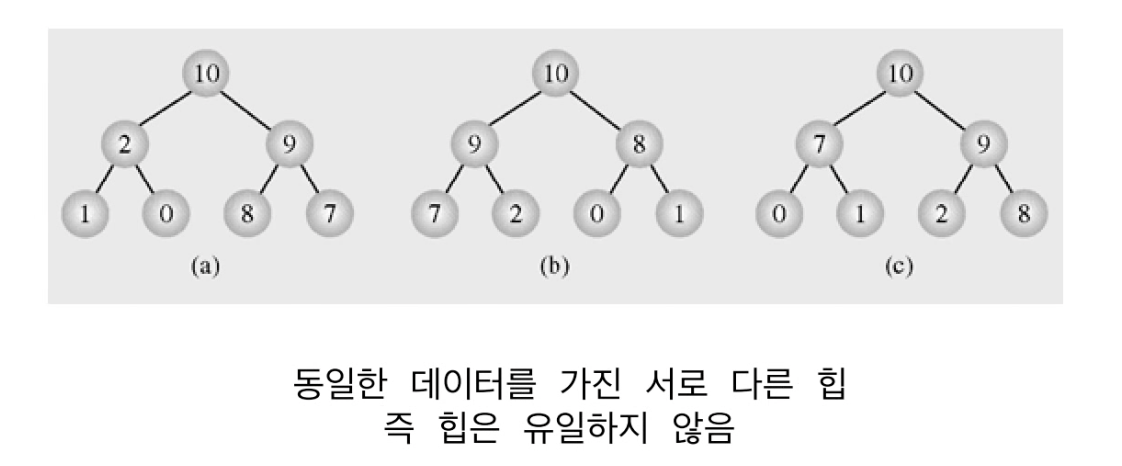
Heap의 표현(배열)

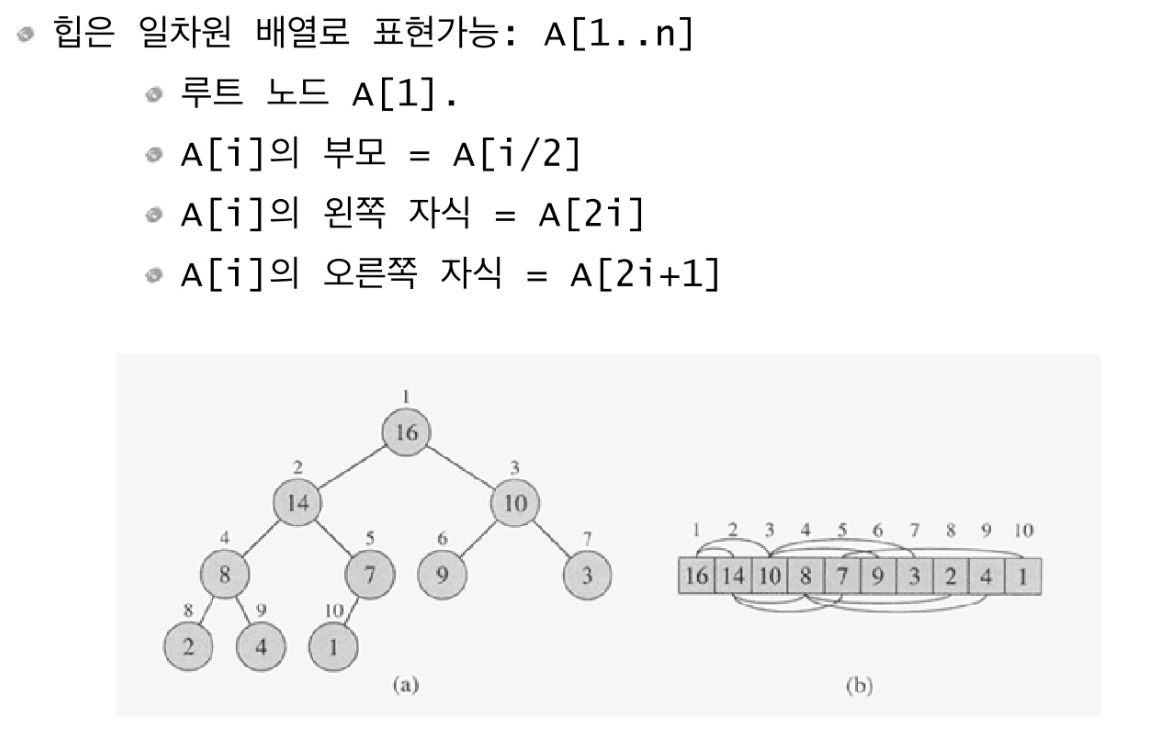
2. Heapify란?

유일하게 root node만이 heap의 조건을 만족하지 않는 상황에서,
heap의 조건을 만족하도록 조작함
Max-heapify의 예시

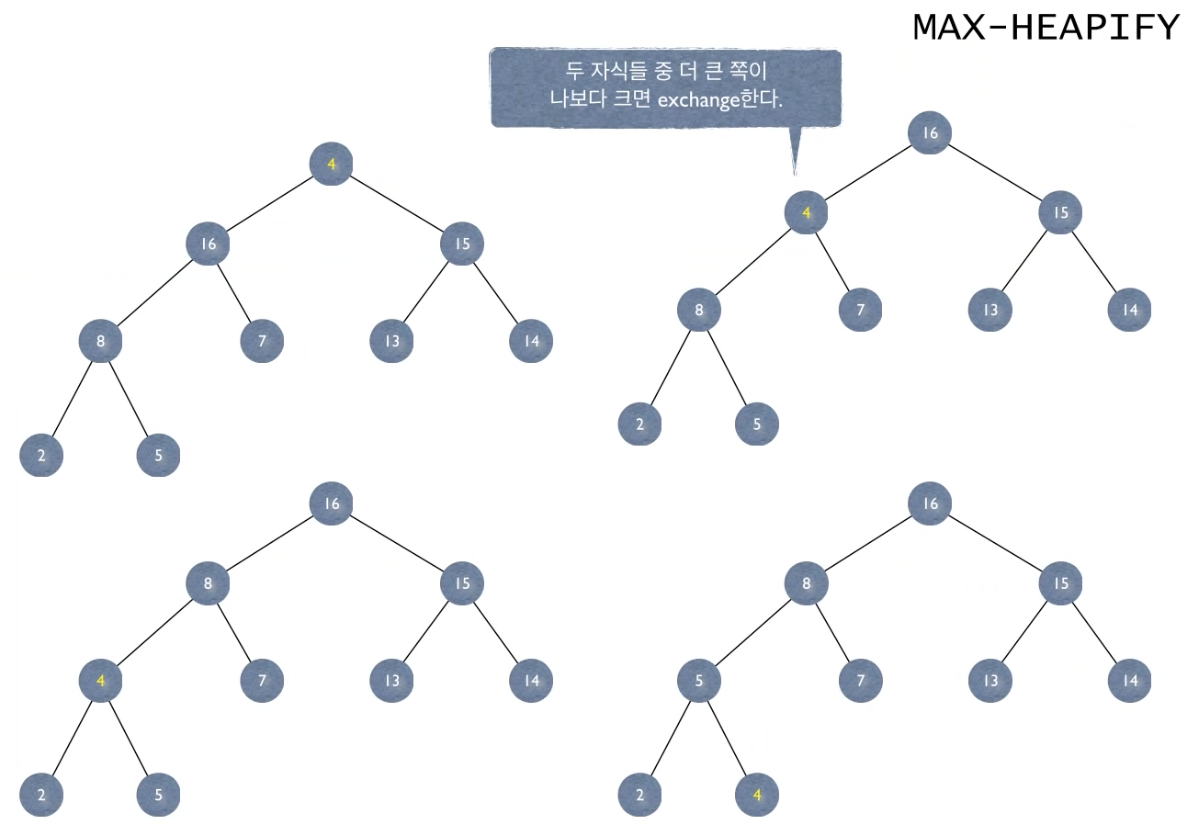
Heapify - Recursion

Heapify - Iteration

3. 정렬할 배열을 힙으로 변환하기

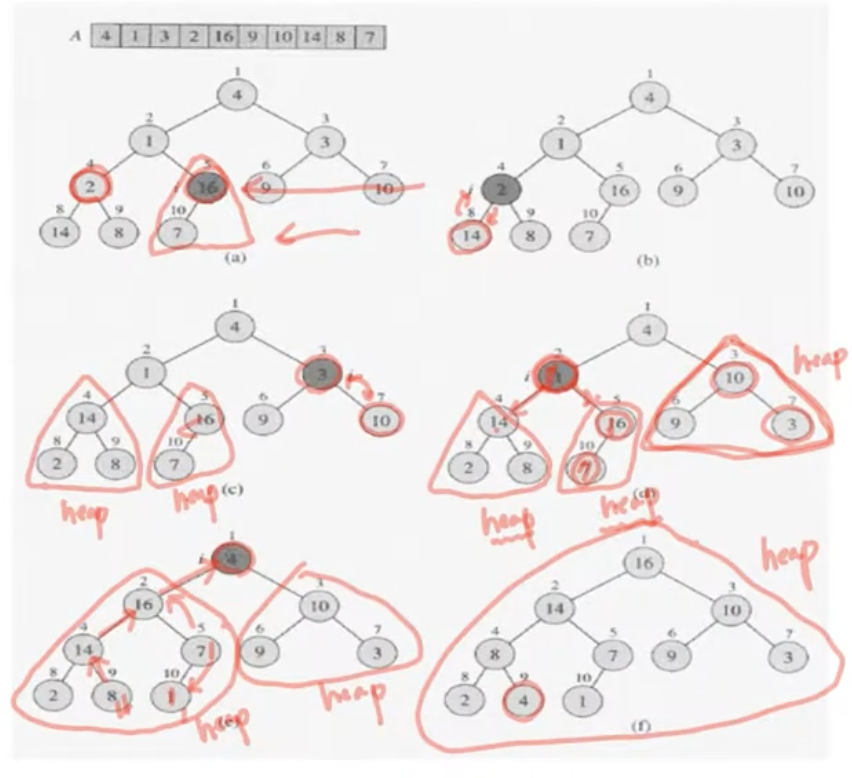
정렬할 배열을 뒤에서부터 역순으로 보면서, leaf 노드가 아닌 첫 노드(k)를 찾음
찾은 노드에 대해 heapify를 수행하고 계속해서 역순으로 올라가며 heapify를 수행함
k = (마지막 노드 - 1) / 2)의 내림값 즉, k = Math.floor((arr.length - 2) / 2)
* 위는 index를 0부터 시작하는 경우임
* index를 1부터 시작하는 경우, k = Math.floor((arr.length - 1) / 2)
예시

4. 힙소트 | Heap Sort

최악의 경우 시간복잡도 O(nlong2n)
sorts in place - 추가 배열 불필요
이진 힙(binary heap) 자료구조를 사용

힙 정렬 로직(순서)

주어진 데이터(배열)을 힙으로 만든다.
힙에서 최대값(루트)를 가장 마지막 값과 바꾼다.
힙의 크기가 1 줄어든 것으로 간주한다. 즉, 가장 마지막 값은 힙의 일부가 아닌 것으로 간주한다.
루트노드에 대해서 Heapify(1)한다
2~4번을 반복한다.

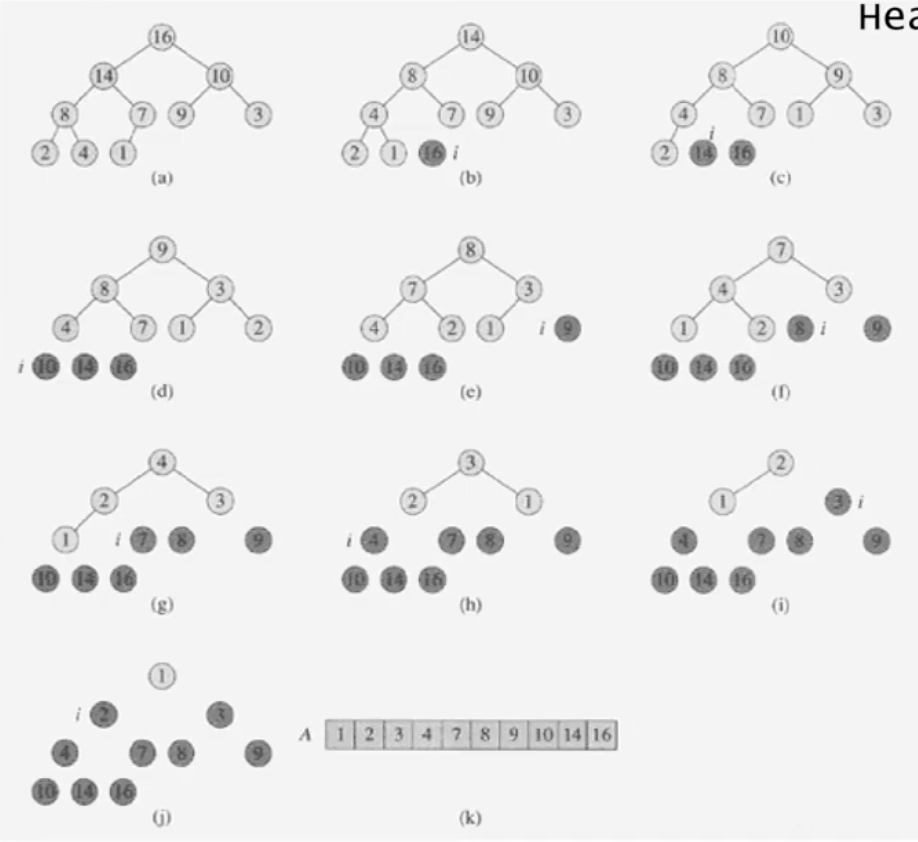
힙 정렬 구현

function heapify(arr) {
  const length = arr.length
  // length가 1보다 작거나 같다면 이미 완전이진트리이며 heap의 조건에 만족함
  if (length <= 1) return;   
  // length가 1보다 큰 경우, 
  // leaf노드가 아닌 첫 노드 = arr의 마지막 leaf 노드의 부모 노드
  // = Math.floor((length - 2) / 2) (*이하 k라고 칭함)
  // k에서부터 값을 1씩 줄이면서 첫번째 인덱스까지 내려갈 것이고,
  // 각각의 값들을 heapifyDown처리함.
  for (let i = Math.floor((length - 2) / 2); i >= 0; i--) {
    heapifyDown(arr, i, length)
  }
  return arr
}

function heapifyDown(arr, i, length) {
  let left = i * 2 + 1
  let right = i * 2 + 2
  let parent = i
  let temp = null

  // left 먼저 비교해보고 더 큰 값이라면 바꾸고
  if (left < length && arr[left] > arr[parent]) {
    parent = left
  }
  // right도 비교해보고 더 큰 값이면 또 바꾸고
  // 아니라면 left 값이 남아 있음
  if (right < length && arr[right] > arr[parent]) {
    parent = right
  }
  // 현재 parent 값은 i | left | right 의 값중 최대 값의 index가 들어있는 상태
  // parent와 i가 같다면 그냥 두면 끝나고
  // 다르다면 현재 i가 최대 값이 아니라는 뜻이므로, parent에 기록해둔 값으로 swap
  // swap해서 내려보낸 값에 대해서 heapifyDown을 다시 실행해줌.
  if (parent !== i) {
    temp = arr[parent]
    arr[parent] = arr[i]
    arr[i] = temp
    heapifyDown(arr, parent, length)
  }
}

function heapSort(arr) {
  const length = arr.length
  if (length === 1) return arr

  let temp = null
  temp = arr[length - 1]
  arr[length - 1] = arr[0]
  arr[0] = temp

  // 최대값을 마지막 값과 swap을 한 상태이기 때문에
  // length에서 -1을 해주어 heapifyDown에서 비교하지 않게 막음
  // 기껏 마지막으로 밀어 놓은 최대값을 다시 퍼올리면 안되겠져?
  heapifyDown(arr, 0, length - 1) 
  return [...heapSort(arr.slice(0, arr.length - 1)), arr[arr.length - 1]]
}


// Test Code
const arr = [31, 8, 48, 8, 73, 11, 3, 20, 8, 29, 65, 15]

const heapifiedArr = heapify(arr) // 배열 => 힙 전환
console.log(heapifiedArr);
// [73, 65, 48, 20, 31, 15, 3, 8, 8, 29, 8, 11]

const heapSortedArr = heapSort(arr) // 힙 정렬
console.log(heapSortedArr);
// [3, 8, 8, 8, 11, 15, 20, 29, 31, 48, 65, 73]

힙 응용: 우선순위 큐 | Priority Queue

Insert(x)

새로운 원소 x를 삽입

function insert(arr, data) {
  arr.push(data)
  let i = arr.length - 1
  let temp = null
  while (i > 0) {
    const parent = Math.floor((i - 1) / 2)
    if (arr[parent] < arr[i]) {
      temp = arr[parent]
      arr[parent] = arr[i]
      arr[i] = temp
      i = parent
    }
  }
  return arr
}

const heap = [7, 4, 6, 1, 3]
console.log(insert(heap, 8)); // [8, 4, 7, 1, 3, 6]

Extract_Max()

최대값을 삭제하고 반환

function heapifyDown(arr, i, length) {
  let left = i * 2 + 1
  let right = i * 2 + 2
  let parent = i
  let temp = null

  if (left < length && arr[left] > arr[parent]) {
    parent = left
  }
  if (right < length && arr[right] > arr[parent]) {
    parent = right
  }
  if (parent !== i) {
    temp = arr[parent]
    arr[parent] = arr[i]
    arr[i] = temp
    heapifyDown(arr, parent, length)
  }
}

function extractMax(arr) {
  let length = arr.length
  let temp = arr[0]
  arr[0] = arr[length - 1]
  arr[length - 1] = temp
  const max = arr.pop()
  heapifyDown(arr, 0, length)
  return max
}

const arr = [7, 4, 6, 1, 3]
console.log(extractMax(arr)); // 7
console.log(arr); // [6, 4, 3, 1]]