'통계 101x데이터분석' 책을 읽고 중요한 내용을 정리했습니다.
3.1 데이터 유형
-
변수
: 공통의 측정 방법으로 얻은 같은 성질의 값
: 각각 다른 값을 취할 수 있으므로 변수라 불림.
ex. 키
: 변수의 개수는 '차원'이라 표현되기도 한다. -
다양한 데이터 유형
: 데이터를 수집할 때나 분석을 실행할 때는 변수가 어떤 유형인지 주의 깊게 고려하는 것이 중요하다. -
변수(양적변수/질적변수)
1) 양적변수
: 숫자로 나타낼 수 있는 변수
: 숫자이므로 대소관계가 있으며 평균값처럼 양을 계산할 수 있다.
: 이산형과 연속형으로 나뉜다.
i) 이산형 양적변수
얻을 수 있는 값이 점점이 있는 변수.
ex. 주사위눈, 횟수
ii) 연속형 양적변수
키 173.4cm나 몸무게 65.8kg 같이 간격 없이 이어지는 값으로 나타낼 수 있는 변수2) 질적변수
숫자가 아닌 범주로 변수를 나타낼 때
ex. 설문조사의 예/아니요, 동전의 앞/뒤, 맑음/흐림/눈/비 등과 같은 날씨, 식당메뉴 등
3.2 데이터 분포
- 도수분포도(히스토그램)
: 데이터 분포를 그림으로 나타내는 데는 어떤 값이 데이터에 몇 개 포함되어 있는가(도수, 빈도, 횟수)를 나타내는 그래프인 도수분포도를 자주 사용
1) 이산형 양적 변수의 히스토그램
: 가로축은 숫자, 세로축은 데이터에 나타난 개수(도수, 빈도, 횟수)를 표시.
ex. 주사위의 눈
2) 연속형 양적 변수의 히스토그램
: 소수점 이하 자리가 얼마든지 지속되기 때문에 엄밀하게 같은 값은 존재하지 않는다. 그러므로 범위를 설정하고, 그 범위에 포함되는 숫자 개수를 세어 이를 세로축에 둔다. 이 범위의 넓이를 '구간폭(bin width)'라고 부른다.
ex. 키
3) 범주형 변수의 히스토그램
: 가로축에는 각 범주를, 세로축에는 각 범주에 속하는 개수를 나타낸다. 범주형 변수의 값에는 대소 관계가 없으므로, 가로축 순서에 특별한 뜻은 없다.
ex. 가로축에 짜장면, 짬뽕
※ 연속변수의 히스토그램에서 주의할 점
: 구간폭을 어떻게 설정하는지에 따라 인상이 달라진다. 히스토그램은 대략적인 데이터 구성을 파악하는 것이 목적이지, 무엇인가 결론을 내기 위한 것이 아니다.
3.3 통계량
- 데이터 특징 짓기
1) 통계량
: 수집한 데이터로 이런저런 계산을 수행하여 얻은 값
2) 기술통계량(요약통계량)
: 데이터 그 자체의 성질을 기술하고 요약하는 통계량.
: 주로 양적 변수를 대상으로 계산한다.
ex. 평균값
: 범주형 변수인 경우, '특정 범주의 값이 몇 개인지' 같은 개수(또는 비율)로만 데이터를 기술하고 요약할 수 있다.
3) 통계량과 정보
: 1개 또는 몇 개의 통계량으로 요약한다는 것은 데이터에 있는 정보 중 버리는 부분이 있다는 것을 의미한다.
ex. 평균값에는 '어느 정도 데이터가 퍼져 있는지'의 정보는 불포함
- 다양한 기술통계량
대푯값: 평균값, 중앙값, 최빈값
데이터 퍼짐 정도를 나타내는 값: 분산, 표준편차
1) 대푯값(representative value)
: 대략적인 분포 위치, 즉 대표적인 값을 정량화하기 위해 사용하는 통계량
i) 평균값(mean)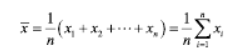
ii) 중앙값(median)
: 크기 순으로 값을 정렬했을 때 한가운데 위치한 값
iii) 최빈값(mode)
: 데이터 중 가장 자주 나타나는 값2) 대푯값의 모습
: 분포가 좌우대칭에 가까운 봉우리 형태라면 평균값, 중앙값, 최빈값은 대체로 일치한다.
: 분포가 좌우 비대칭 분포하면 각각 다른 값이 되는 경향이 있다.
※ 평균값은 계산 시 모든 값을 고려하기 때문의 이상값(outlier)의 영향을 받기 쉽다.
3) 히스토그램의 중요성
: 처음부터 히스토그램을 그려 대략적인 파악을 한 다음, 대푯값으로 적절하게 분포를 특징지을 수 있는지 확인하는 것이 데이터 분석작업 순서라는 것을 꼭 기억해두자.
4) 분산과 표준편차
: 데이터 퍼짐을 평가하기 위해 분산 혹은 표준편차라는 통계량을 계산한다
i) 분산(s^2)
: 표본의 각 값과 표본평균이 어느 정도 떨어져 있는지를 평가하는 것으로, 데이터 퍼짐 상태를 정량화한 통계량
: 각 값과 평균값 사이 거리의 제곱을 평균화한 값으로써 데이터 퍼짐 정도를 평가.
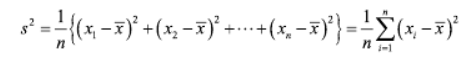
아래는 분산의 성질

ii) 표준편차(s)
: 분산의 제곱근을 취한 값
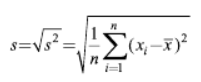
분산의 예)
데이터 분포의 넓이가 넓어질수록, 그에 따라 분산과 표준편차가 커진다. 시험 점수처럼 학력의 차이를 측정할 때는, '0점부터 100점까지 다양한 값이 나오는 테스트'쪽이 바람직한 시험이라 할 수 있다.
3.4 확률
1) 확률의 기본 사고방식
: 확률이란? (발생여부가) 불확실한 사건의 발생 가능성을 숫자로 표현한 것
: 각 사건의 확률 P는 0 이상 1 이하의 실수로, 큰 값일수록 발생하기 쉽다는 뜻
: 모든 사건의 확률을 전부 더하면 1이 된다.
ex. 변수 ={붉은 구슬, 흰 구슬}이라 하면, P(X= 붉은 구슬) = 4/5, P(X= 흰 구슬) = 1/5
2) 확률변수
: 확률이 달라지는 변수. 위의 예에서 X
: cf) 실현값이란? 확률변수가 실제로 취하는 값. 위의 예에서 붉은 구슬 또는 흰 구슬
: 이산형 확률변수(ex. 주사위 눈) / 연속형 확률변수(ex. 키와 같이 연속한 값)
3) 확률분포
: 가로축에 확률변수를, 세로축에 그 확률변수의 발생가능성을 표시한 분포
: 확률변수가 이산형인 경우, 세로축이 확률 그 자체를 나타낸다.
: 히스토그램과 마찬가지로 확률변수가 범주일 때는 세로축 순서에 의미는 없다.
4) 확률밀도함수
: 연속형 확률변수의 경우에는 값에 일정한 범위를 두고 확률을 구한다. 그 확률을 계산하는 함수가 '확률밀도함수'
: 세로축은 확률 그 자체의 값이 아니라, 상대적인 발생 가능성을 표현한 값.
: 확률변수가 어떤 값에서 어떤 값까지의 범위에 들어갈 확률을 알고 싶다면, 확률밀도함수를 적분하여 x축과 확률밀도함수로 둘러싸인 부분의 넓이를 구하면 된다. 이 넓이가 바로 확률이다.
: 확률별수의 정릐역 전체를 적분하면 1이 되며, 곧 모든 사건 중 어느 것이든 일어날 확률이 1이라는 것을 나타낸다.
5) 추론통계와 확률분포
: 현실 세계의 모집단을 수학 세계의 확률분포로 가정하고, 표본 데이터는 그 확률분포에서 생성된 실현값인 것으로 가정하여 분석을 진행
: 이렇게 함으로써 '모집단과 표본 데이터'처럼 다루기 어려운 대상이 '확률분포와 그 실현값'처럼 다룰 수 있는 대상으로 치환되는 것
: 통계적 추론이란, 얻은 데이터로부터 그 발생원이 어떤 확률분포를 취하는지를 추정하는 것
6) 기댓값(expected value)
: '변수가 확률적으로 얼마나 발생하기 쉬운가'를 평균적인 값으로 나타냄

7) 분산
: 분산이란? 확률분포가 기댓값 주변에 어느 정도 퍼졌는지를 나타내는 값
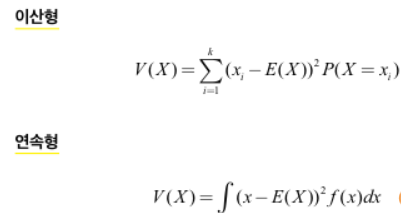
: 두 식은 각각 기댓값과의 차이를 제곱한 숫자를 이용해 데이터가 기댓값에서 어느 정도 떨어져 있는지를 평가함
8) 표준편차
: 분산 V(X)의 제곱근을 취한 값
9) 분산과 표준편차의 성질

10) 왜도와 첨도
: 왜도(skewness)란? 분포가 좌우대칭에서 어느 정도 벗어났는지로 평가
: 첨도(kurtosis)란? 분포가 얼마나 뾰족한지와 그래프의 꼬리가 차지하는 비율(분포의 양쪽 끝 꼬리의 확률 크기)이 얼마인지로 평가
11) 확률변수가 2개일 때
: 확률변수 2개를 동시에 생각할 때의 확률분포를 동시확률분포 P(X, Y)라 한다.
i) 독립
: X와 Y 2개 확률변수가 독립이라는 말은, X와 Y의 동시확률분포 P(X, Y)가 각각의 확률 P(X)와 P(Y)의 곱과 같다는 뜻
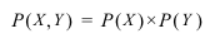
: 이는 한쪽이 어떤 값을 취하든지, 다른 한쪽의 발생 확률은 변하지 않는다는 것을 의미한다.
ii) 조건부확률
: 한쪽 확률변수 Y의 정도가 주어졌을 때, 다른 한쪽 확률변수 X의 확률을 조건부확률 P(X|Y)라 한다.(P(X=조건|Y=확률변수))
ex. X를 상의, Y를 하의로 하여, 반드시 카키색 바지에는 검은색 티셔츠 흰색바지에는 분홍색 티셔츠를 맞춰입는 사람이 있다면

3.5 이론적인 확률분포
1) 이론적인 확률분포
: 수식으로 표현되며, 분포의 형태를 정하는 파라미터(parameter, 모수)를 가진다. 그러므로 파라미터를 알면 확률분포의 형태를 알 수 있다.
2) 정규분포(normal distribution) = 가우스 분포(Gaussian distribution)
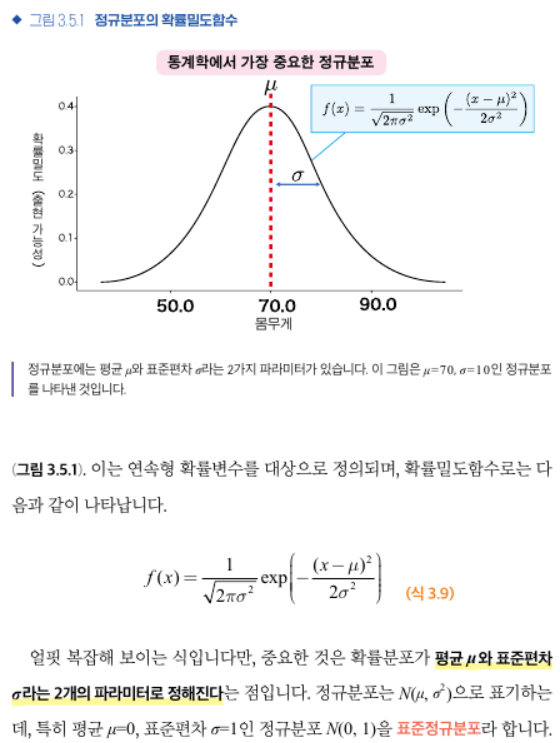
: μ는 분포의 위치를, σ는 분포의 넓이를 결정한다.
3) 정규분포의 특징

4) 정규분포의 성질

: 이러한 특징과 성질은 μ나 σ의 값이 달라져도 변하지 않는다.
ex. 
-> 153.6cm 이하 또는 181.6cm 이상인 사람은 약 5% 정도라는 걸 알 수 있다.
-> '188.6cm는 평균에서 3σ 떨어져있다.'는 약 0.3%(상위 0.15%)에 속하는 드문값이라는 의미를 전달할 수 있다.
5) 표준화(standardizing, normalizing)
: 일반적으로 확률변수 x 또는 데이터의 평균 μ(x̄)와 표준편차 σ(s)를 이용하여 다음과 같이 계산하면 평균 0, 표준편차 1로 변환할 수 있다.
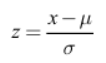
: 변환된 새로운 값을 z값이라 부르기도 한다.
: 평균과의 거리가 표준편차의 몇 배인가를 나타내기 때문에, 본래의 μ나 σ와 상관없이 분포 안에서 어디에 위치하는가를 알 수 있다.
: 평균과 표준편차에 기준을 두고 데이터를 나열하는 것으로, 본래 점수 자체가 아닌 분포 안에서의 위치로 평가할 수 있게 된다.
