트리

ppparkta·2022년 3월 29일

자료구조

목록 보기

7/9

*이 글은 2022년 1월~2월 노션으로 진행한 스터디를 옮긴 글입니다.

220124 트리 내용정리(220125내용추가)

트리 개념 정리
- 루트노드: 트리구조 최상위에 존재하는 노드
- 노드: 트리의 구성요소
- 엣지: 노드와 노드를 연결하는 선
- 터미널 노드(=리프 노드): 말단 노드
- 서브트리: 큰 트리(전체)에 속하는 작은 트리
- 레벨: 트리의 각 층별로 숫자를 매긴 것
- 이진트리: 루트노드를 중심으로 둘로 나뉘는 두개의 서브트리도 이진트리여야 하고, 서브트리의 모든 서브트리도 이진트리여야 함
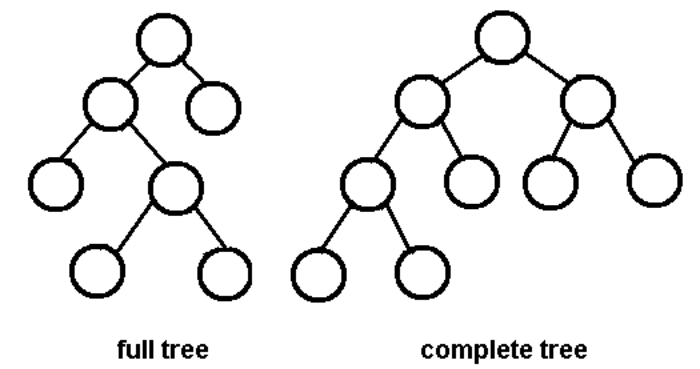
- 포화이진트리: 모든 레벨이 꽉 찬 이진트리
- 완전이진트리: 포화이진트리처럼 모든 레벨이 꽉 찬 상태는 아니지만 차곡차곡 빈 틈 없이 노드가 채워진 이진 트리. 즉 포화이진트리는 완전이진트리에 포함관계임.

트리의 순회(백준1991)

전위순회: 루트노드→왼쪽서브트리→오른쪽서브트리
중위순회: 왼쪽서브트리→루트노드→오른쪽서브트리
후위순회: 왼쪽서브트리→오른쪽서브트리→루트노드
왜 안되나 하고 몇십분 붙잡고 있었는데 복붙하다가 left를 right로 안 바꿔줘서 문제가 발생함-_-................

트리 구성하는 방법이 도저히 감이 안 잡혀서 트리 구성하는 부분은 다른 사람 코드 참고함. vector STL사용. 그 외 순회는 재귀함수 사용.

**//수정 전**
#include<iostream>
#include<vector>
using namespace std;

class Node {
public:
	char left;
	char right;
};

const int MAX_SIZE = 26;
vector<Node> tree(MAX_SIZE);

//전위순회 루트->왼->오
void beforeV(char pa) {
	if (pa == '.')return;
	else {
		cout << pa;
		beforeV(tree[pa-'A'].left);
		beforeV(tree[pa-'A'].right);
	}
}
//중위순회 왼->루트->오
void middleV(char pa) {
	if (pa == '.')return;
	else{
		middleV(tree[pa-'A'].left);
		cout << pa;
		middleV(tree[pa-'A'].right);
	}
}
//후위순회 왼->오->루트
void afterV(char pa) {
	if (pa == '.')return;
	else {
		afterV(tree[pa-'A'].left);
		afterV(tree[pa-'A'].left);
		cout << pa;
	}
}

int main() {
	int number;
	cin >> number;
	char pa, chL, chR;
	for (int i = 0; i < number; i++) {
		cin >> pa >> chL >> chR;
		tree[pa-'A'].left = chL;
		tree[pa-'A'].right = chR;
	}
	beforeV('A');
	cout << endl;
	middleV('A');
	cout << endl;
	afterV('A');
	return 0;
}

**//수정 후**
#include<iostream>
#include<vector>
using namespace std;

class Node {
public:
	char left;
	char right;
};

const int MAX_SIZE = 26;
vector<Node> tree(MAX_SIZE);

//전위순회 루트->왼->오
void beforeV(char pa) {
	if (pa == '.')return;
	else {
		cout << pa;
		beforeV(tree[pa-'A'].left);
		beforeV(tree[pa-'A'].right);
	}
}
//중위순회 왼->루트->오
void middleV(char pa) {
	if (pa == '.')return;
	else{
		middleV(tree[pa-'A'].left);
		cout << pa;
		middleV(tree[pa-'A'].right);
	}
}
//후위순회 왼->오->루트
**void afterV(char pa) {
	if (pa == '.')return;
	else {
		afterV(tree[pa-'A'].left);
		afterV(tree[pa-'A'].right);
		cout << pa;
	}
}**

int main() {
	int number;
	cin >> number;
	char pa, chL, chR;
	for (int i = 0; i < number; i++) {
		cin >> pa >> chL >> chR;
		tree[pa-'A'].left = chL;
		tree[pa-'A'].right = chR;
	}
	beforeV('A');
	cout << endl;
	middleV('A');
	cout << endl;
	afterV('A');
	return 0;
}

수식트리 계산

/*
트리 구조 
 +
 *+
3256
**후위순회방식으로 방문하여 연결**
*/
#include<iostream>
using namespace std;

class Node {
public:
	int data;
	Node* left;
	Node* right;
	Node(int x) {
		data = x;
		left = right = NULL;
	}
};

//후위순회하여 수식 계산
//재귀함수 사용시 끝나는 조건을 분명히 명시할 것
//반복수행되는 과정 일일히 생각해서 식 작성해보기
int  evaluate(Node* root) {
	if (root->left == NULL && root->right == NULL) return root->data;
	else {
		int op1 = evaluate(root->left);
		int op2 = evaluate(root->right);
		switch (root->data) {
		case'+': return op1 + op2;
		case '-': return op1 - op2;
		case'*':return op1 * op2;
		case'/':return op1 / op2;
		}
	}
	return 0;
}

int main() {
	//트리구성
	//노드7개 생성
	Node* n1 = new Node(3);
	Node* n2 = new Node(2);
	Node* n3 = new Node('*');
	Node* n4 = new Node(5);
	Node* n5 = new Node(6);
	Node* n6 = new Node('+');
	Node* root = new Node('+');
	//6개 가지연결하기
	root->left = n3;
	root->right = n6;
	n3->left = n1;
	n3->right = n2;
	n6->left = n4;
	n6->right = n5;

	int result = evaluate(root);
	cout<<"수식트리의 값: " << result << endl;
}

힙 정리

완전이진트리
모든 노드에 저장된 값들은 자식 노드들의 것보다 크거나 같음
힙으로 우선순위 큐 구현 시 노드에 저장된 값을 우선순위로 봄
즉 데이터가 크던 작던 우선순위가 높을수록 루트 노드와 가깝게 자리잡게 됨.
배열 기반으로 구현하는 것이 용이함. 완전이진트리이므로 연결리스트 사용해도 되지만 배열이 편함. 단, 인덱스는 1부터 사용함. (0부터 시작할 시 굳이 연산 추가해야 함)

우선순위 큐 구현 시 힙 사용하는 이유?→

구현방법	삽입	삭제
배열	O(1)	O(N)
연결리스트	O(1)	O(N)
힙	O(logN)	O(logN)

**//최소 힙**
#include<iostream>
using namespace std;

const int MAX_SIZE = 100;
int heap[MAX_SIZE];

void push(int item, int* n) {
	int i = 0;
	i = ++(*n);
	/*
	개념은 부모-자식 간 비교하며 즉시 서로 자리를 바꾸는 것임.
	그러나 실제로 코드를 구현할 시 들어올 자식보다 작았던 부모는 먼저 그 자리로 바꾸고
	 while문 빠져나올 때 새로 들어올 자식을 최종적으로 넣으면 됨.
-힙 끝에 새 요소를 삽입
-부모 노드와 비교하여 힙 속성을 위배하는 경우 부모 노드와 값을 바꿈
-힙 속성이 유지될 때까지 2번 작업을 반복
	*/
	while ((i != 1) && item < heap[i / 2]) {
		heap[i] = heap[i / 2];
		i = i / 2;
	}
	heap[i] = item;
}

int delete_de(int* n) {
	int first, temp, parent, child;
	first = heap[1];
	temp = heap[(*n)--];
	parent = 1;
	child = 2;
	while (child <= *n) {
		if ((child < *n) && (heap[child] > heap[child + 1])) child++;
		if (temp <= heap[child]) break;
		heap[parent] = heap[child];
		parent = child;
		child *= 2;
	}
	heap[parent] = temp;
	return first;
}

int main() {
	int input;
	int n = 0, count = 0;
	cout << "min heap구현. 숫자를 입력하세요." << endl << "***숫자입력(-1 입력시 입력 종료)***" << endl;

	while (1) {
		cin >> input;
		if (input == -1) break;
		push(input, &n);
		count++;
	}
	cout << "level order traversal: ";
	for (int i = 1; i <= count; i++) {
		cout << heap[i]<<" ";
	}
	cout << endl;
	cout << "최상위 노드 삭제 값: ";
	cout<<delete_de(&count);
	cout << endl;
	cout << "삭제 후 힙의 level order traversal: ";
	for (int i = 1; i <= count; i++) {
		cout << heap[i] << " ";
	}
	cout << endl;
}

220126 백준5430 AC

알고리즘 구상 고려할 것
- [1,2,3] 방식으로 주어진 배열을 어떻게 받아올 것?
- R함수와 D함수의 기능은 무슨 자료구조로 구현할 것?→vector STL
- 해당 방식을 입력한 테스트케이스만큼 반복하기 위해 필요한 자료는 무엇?→테스트케이스의 횟수만큼 벡터를 준비해야 함.
- 이런게 구현문제구나! 하고 알 수 있었던 문제...무시해서 미안하다. 구현 실패 ㅋㅋ

ppparkta

겉촉속촉

이전 포스트

큐와 덱

다음 포스트

트리

자료구조

220124 트리 내용정리(220125내용추가)

220126 백준5430 AC

큐와 덱

그래프

0개의 댓글