지금까지 알고리즘 문제를 풀면서 시간 복잡도에 대한 개념이 확실히 잡히지 않아
이번 기회에 확실히 하고자 공부해보았다.
항상 여러번 풀다보면 알게 된다. 어느 정도인지 보인다 와 같은 말들을 들어왔는데 아무리 해도 모르겠더라
이렇게 하다보니 제대로 알고 하는 것이 아니라 단순 문제풀이만 하는 것 같고
효율성 문제에 대해 고민을 할 수가 없게 되는 한계를 느꼈다.
시간복잡도 정의
- 빅-오메가 : 최선의 연산 횟수
- 빅-세타 : 평균의 연산 횟수
- 빅-오 : 최악의 연산 회수
사실 처음부터 최선이라는 말과 최악이라는 말이 이해가 되지 않았다.
최선은 무엇을 의미하고 최악은 뭘 얘기하는 것인가, 대충 감은 왔지만 제대로 이해하지 못했음을 이번 학습을 통해 깨달았다.
예를 통해 확인해보자
public class timeComplexity {
public static void main(String[] args){
int num = (int)Math.random() * 100;
for(int i =0; i < 100; i++){
if(num == i) {
System.out.println(i);
}
}
}
}- 빅-오메가 : 1번
- 빅-세타 : N/2번
- 빅-오 : N번
최선이라 함은 가장 빠르게 원하는 답을 찾았을 때를 의미한다. 고로 num값과 i 값이 바로 처음부터 같아지는 순간을 의미하므로 빅-오메가는 한 번이 된다.
평균이라 함은 말그대로 일반적인 것을 의미한다.
최악이라 함은 num과 같은 i를 찾는데 반복문을 끝까지 돌려서 결과값이 나온 경우를 의미하므로 이 경우 최악은 N번이 된다. 여기서 N은 반복횟수를 의미한다.
시간 복잡도의 표기와 활용
위와 같은 이유로 코딩테스트를 위한 알고리즘 사용시에는 모든 테스트케이스를 통과해야하기 때문에 빅-오 표기법을 사용하게 된다.
표기는 O(n)과 같은 방식으로 사용하며 O(nlogn), O(logn), O(n^2)등 다양하게 존재한다.
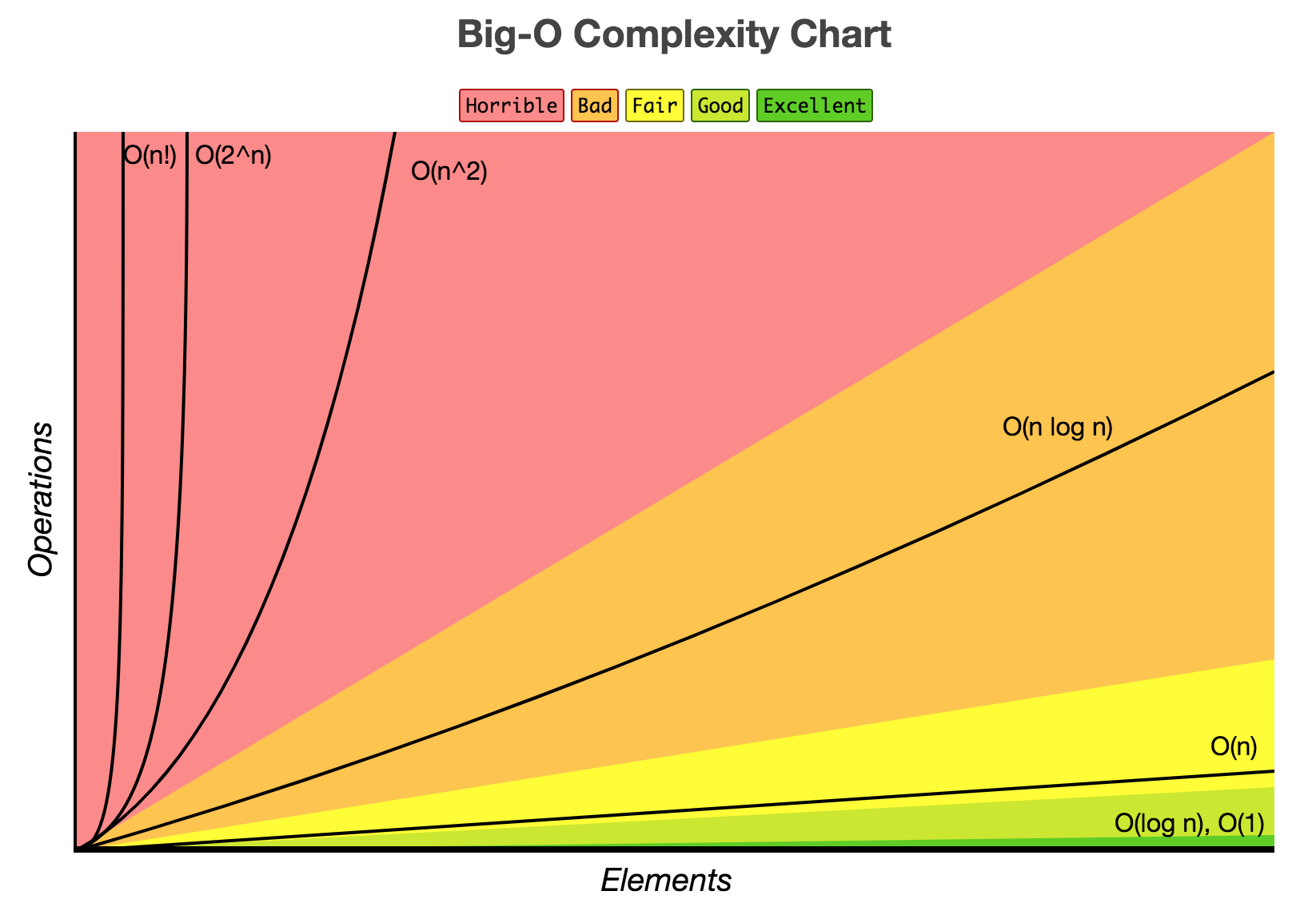
출처 http://bigocheatsheet.com/빅-오 시간 복잡도를 그래프로 나타내면 위와 같다. 팩토리얼의 경우 기하급수적으로 느는 것을 확인할 수 있다.
보통 1억번의 연산에 1초를 걸린다고 가정하므로 시간 복잡도를 계산하여 알맞는 알고리즘을 사용하는 것이 중요하다.
도출기준
- 시간 복잡도에서 상수는 제외한다.
상수는 연산에 큰 영향을 미치지 않으므로, 예를 들어 O(3N)으로 계산되는 경우 O(N)으로 표기한다. - 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.
public class timeCompelxityFor{
public static void main(String[] args){
for(int i =0; i < n; i++){
for(int j = 0; j < n; j++){
System.out.println(i*j);
}
}
for(int i = 0; i < n; i++){
System.out.println(i);
}
}
}위의 예에서 시간 복잡도는 O(n^2)으로 표현할 수 있다.
가장 많이 중첩된 반복문을 기준으로 하기 때문이다.
만약 저 코드에 3중 for문이 추가된다면 그 반복문을 기준으로 시간 복잡도가 계산된다.
자료 출처 및 참고 : Do it!알고리즘 코딩 테스트 - 자바 편이 외에도 시간 복잡도는 더욱 복잡한 개념을 갖고 있는 것 같지만 현 상황에서는 이 정도로도 충분하다고 판단된다.
개인정리이기에 틀린 내용이 있을 수 있습니다. 피드백은 언제나 환영, 맹목적 비난은 삼가주세요