트리 (Tree)
특징
- 트리는 한 노드가 여러 노드를 가르킬 수 있는 비 선형적 자료구조
- 내부적으로 순서를 가질 수 있게 구현 가능하지만 트리에서 순서는 중요하지 않음
- 트리는 계층적인 속성을 표현 가능하게 하고 그래프 자료구조의 일종임
- 폴더 구조 처럼 데이터간의 상하구조를 표현할 때 트리구조를 사용할 수 있다
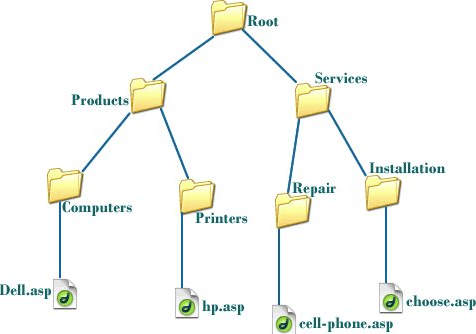
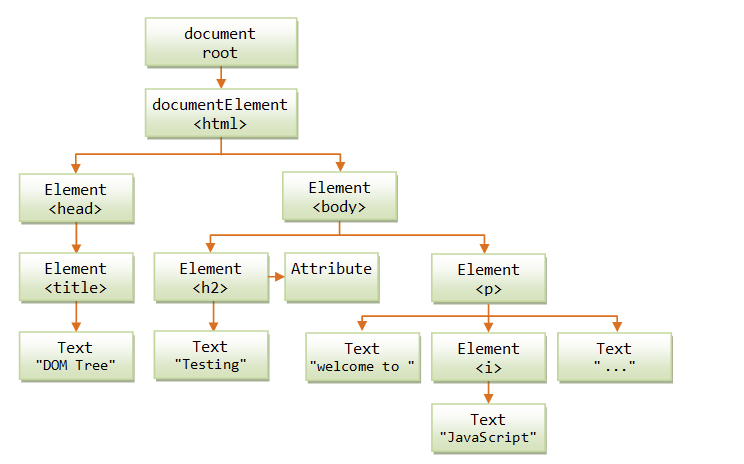
- 트리의 하위 노드는 트리의 또 다른 트리를 가진다는 재귀적인 특징을 가짐
트리에서 사용되는 용어
node
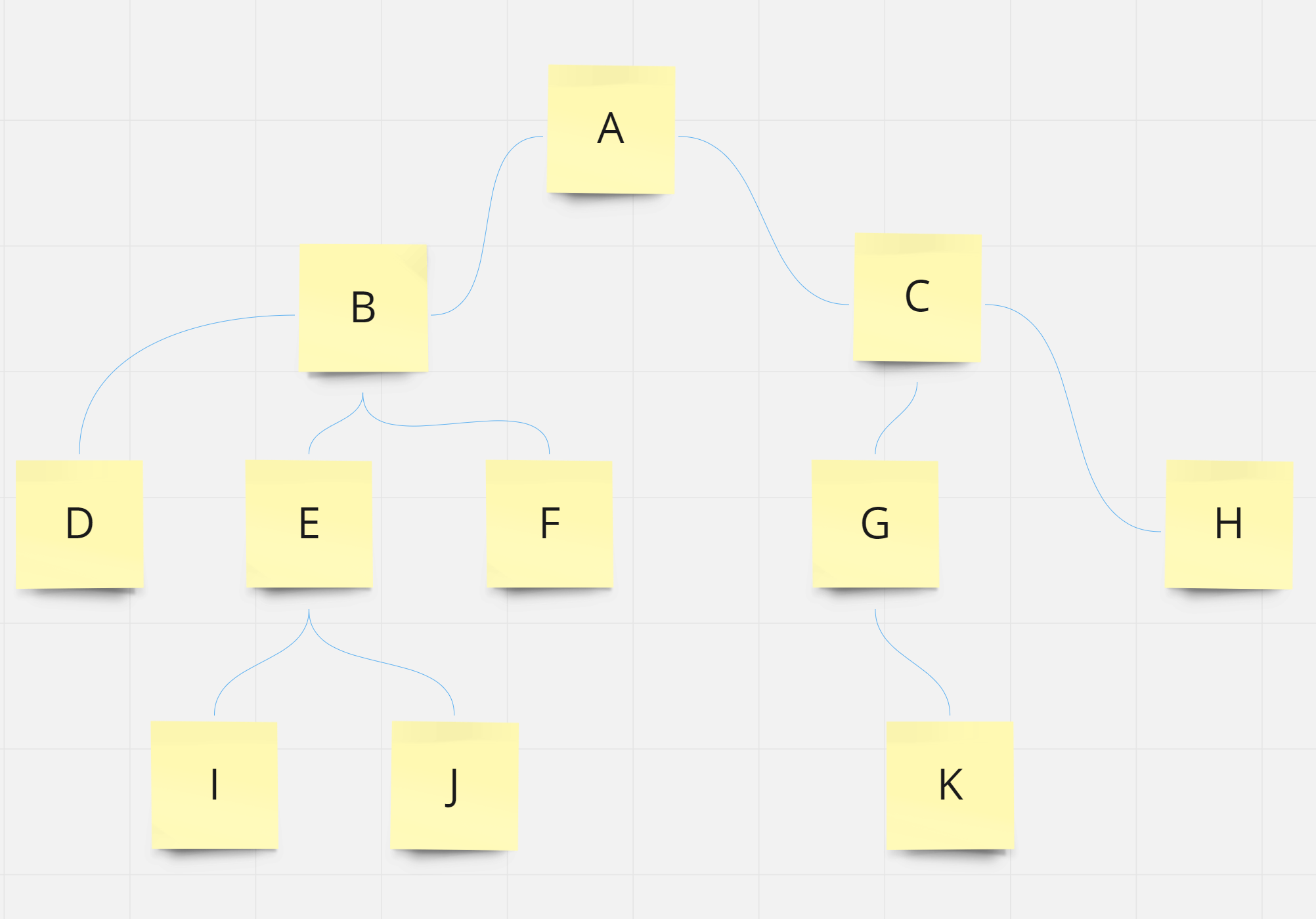

node
- 트리를 구성하는 각 데이터 원소들
root, edge
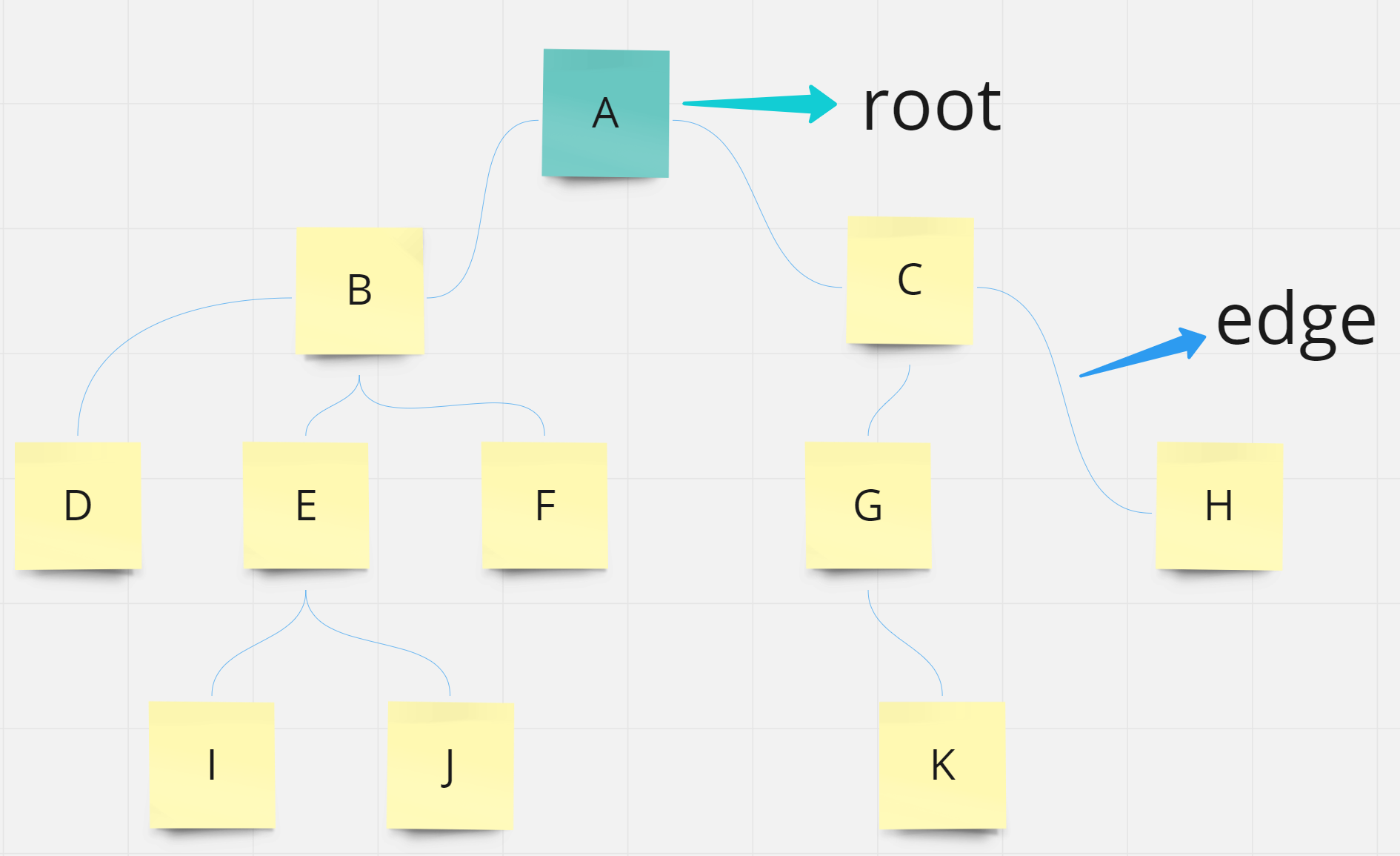

root
- 트리에서 부모가 없는 최상위 노드
- 트리의 시작점
- 최대 한개의 root 노드를 가질 수 있음
edge
- 각 노드를 연결하는 노드 간 선
트리는 root로 부터 구성되어 있고 edge로 연결되어 있다
parent child (sibling), degree, leaf
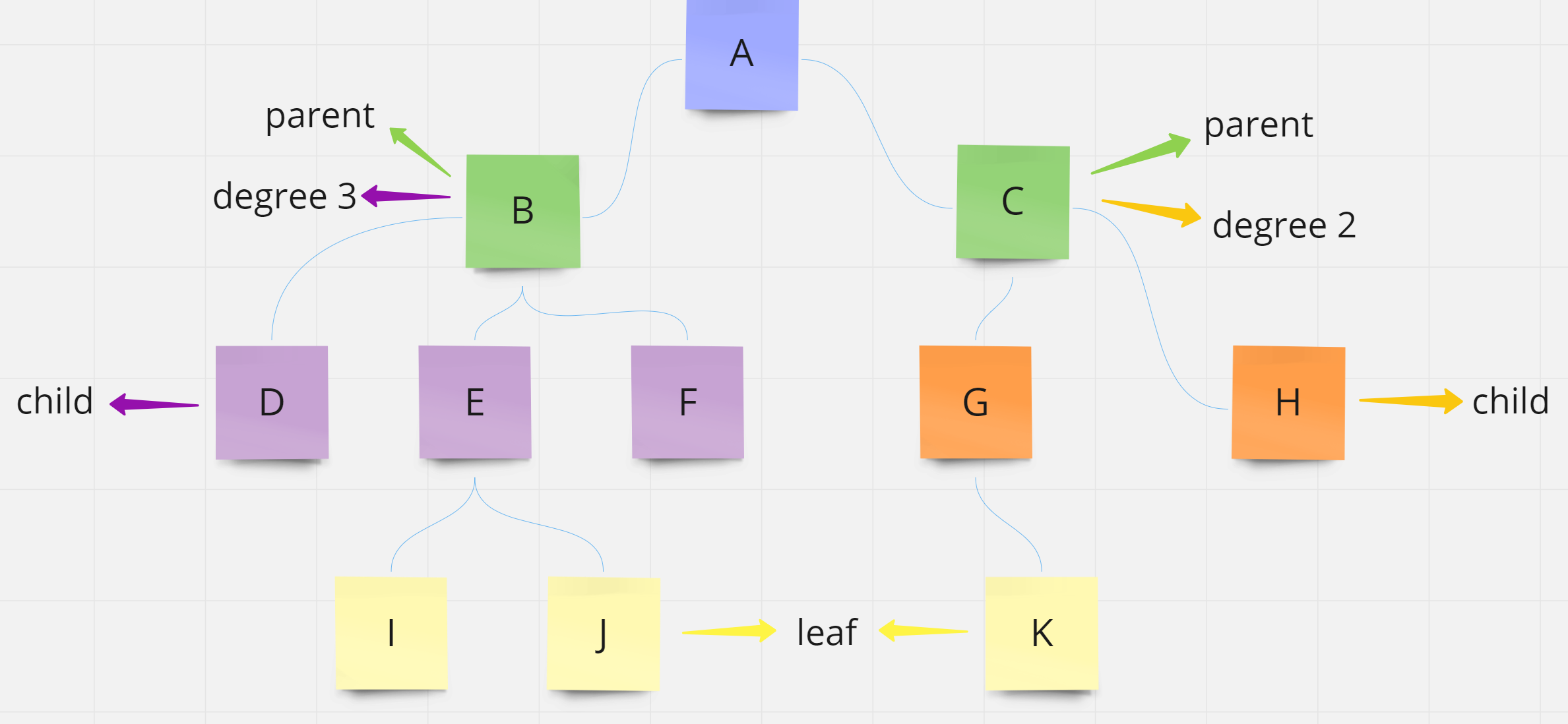

parent child (sibling)
- 트리의 계층적 속성에서 상위에 위치한 노드를 parent 노드, 하위에 위치한 노드를 child 노드, 같은 부모를 가진 노드는 형제노드 라고 부른다
- parent 노드와 child 노드는 상대적인 개념이다
- 즉 누군가의 parent 노드가 될 수 있고 child 노드가 될 수 있음
degree
- 각 노드의 자식수를 나타냄
leaf
- 자식이 없는 노드를 나타냄
- 데이터의 끝 부분을 나타내기 때문에 terminal 노드 라고도 함
depth, level
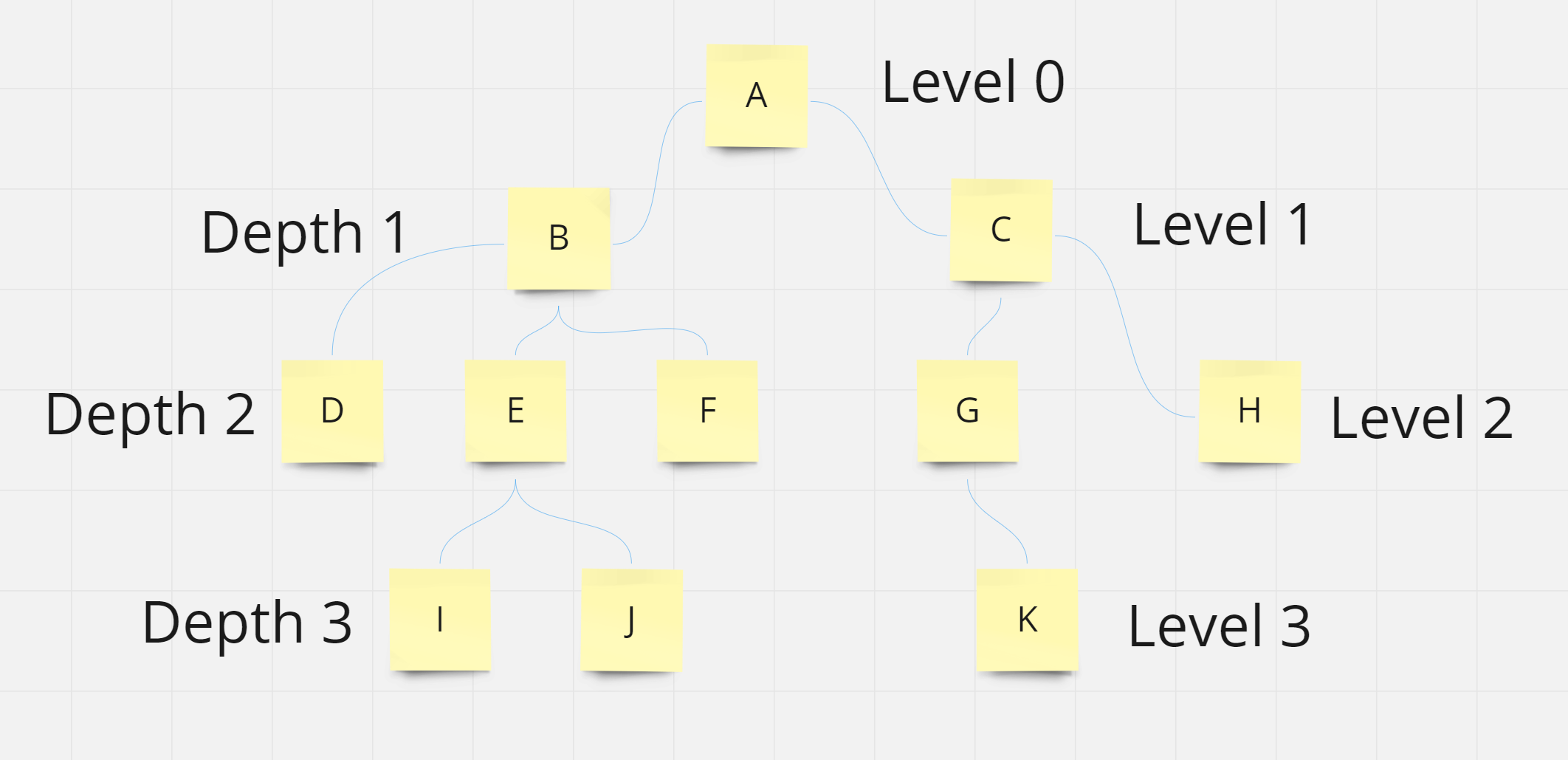

depth
- 각 노드에서 root까지의 거리를 depth라고 함
- 가장 큰 depth는 트리의 높이라고 함 === I, J, K
level
- 같은 depth를 가진 노드의 집합을 level이라고 함
path
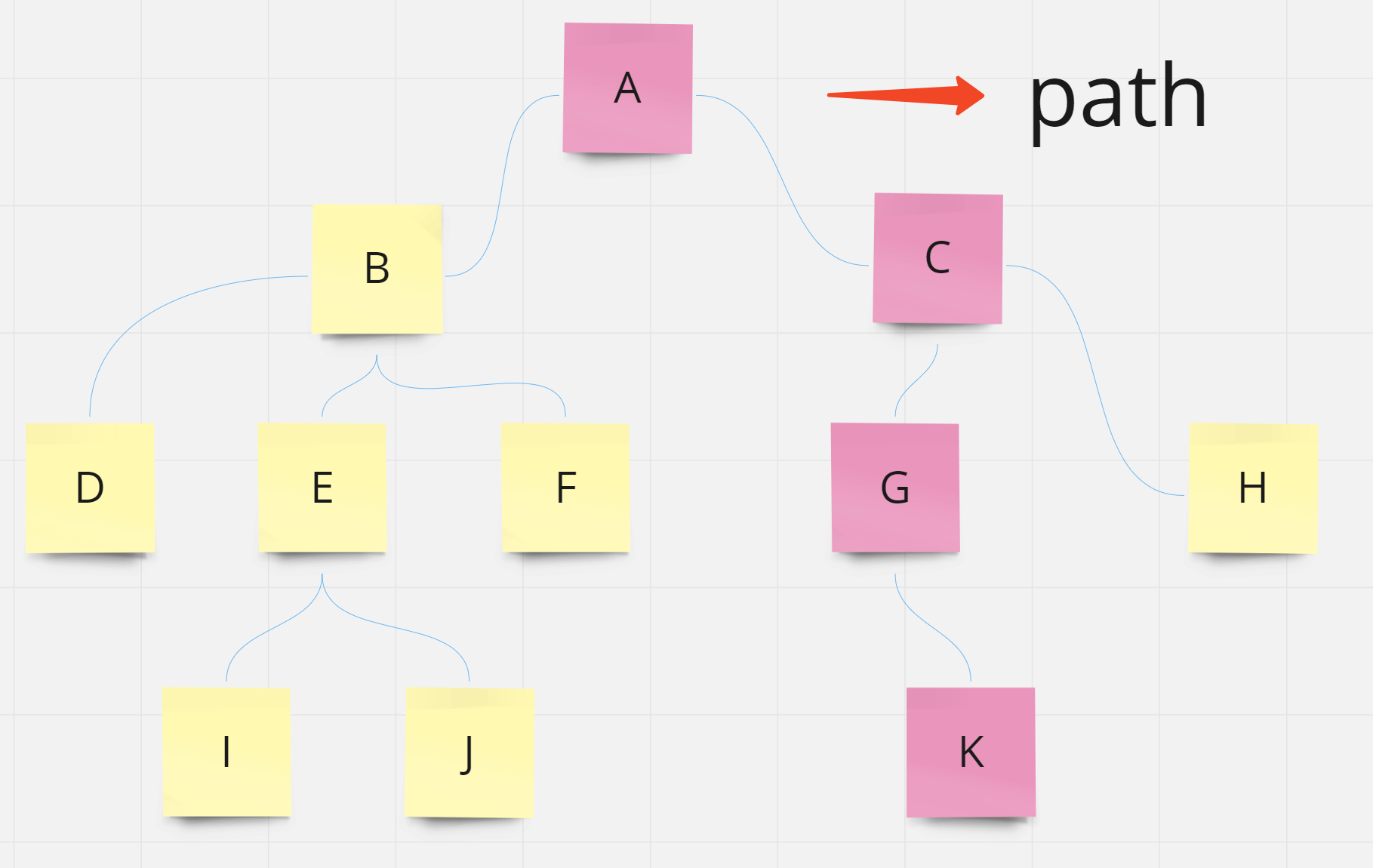

path
- path를 표현할 때 중복노드를 포함하지 않음
- ex) A 부터 F 까지 경로를 표현할 때
= A → C → G → K (O)
= A → C → H → C → G → K (X)
이진트리 (Binary Tree)
특징
- 각 노드가 최대 2개(0개~2개)의 자식 노드를 가지는 트리
- 자식이 없을 수도 있고 있을 수도 있음
- 같은 루트에 같은 자식노드 하나를 가지고 있어도 자식노드의 위치가 각각 왼쪽과 오른쪽으로 다르다면 그 두 투리는 다른 트리가 된다
정이진트리, 엄격한이진트리
- 모든 노드가 2개의 자식을 가지거나 자식이 없을 때
완전이진트리
- 마지막 레벨을 제외하고 모든 노드가 채워져야 함
- 마지막 레벨의 노드는 다 채워질 수도 있고 아닐 수도 있음
- 노드는 왼쪽에서 오른쪽으로 채워짐
- 어느 노드에 오른쪽 자식이 존재한다면 왼쪽 자식도 있어야 함
탐색
전위탐색 preorder
- 노드 방문
- 왼쪽 서브트리 preorder
- 오른쪽 서브트리 preorder
중위탐색 inorder
- 왼쪽 서브트리 inorder
- 노드 방문
- 오른쪽 서브트리 inorder
후위탐색 postorder
- 왼쪽 서브트리 postorder
- 오른쪽 서브트리 postorder
- 노드 방문
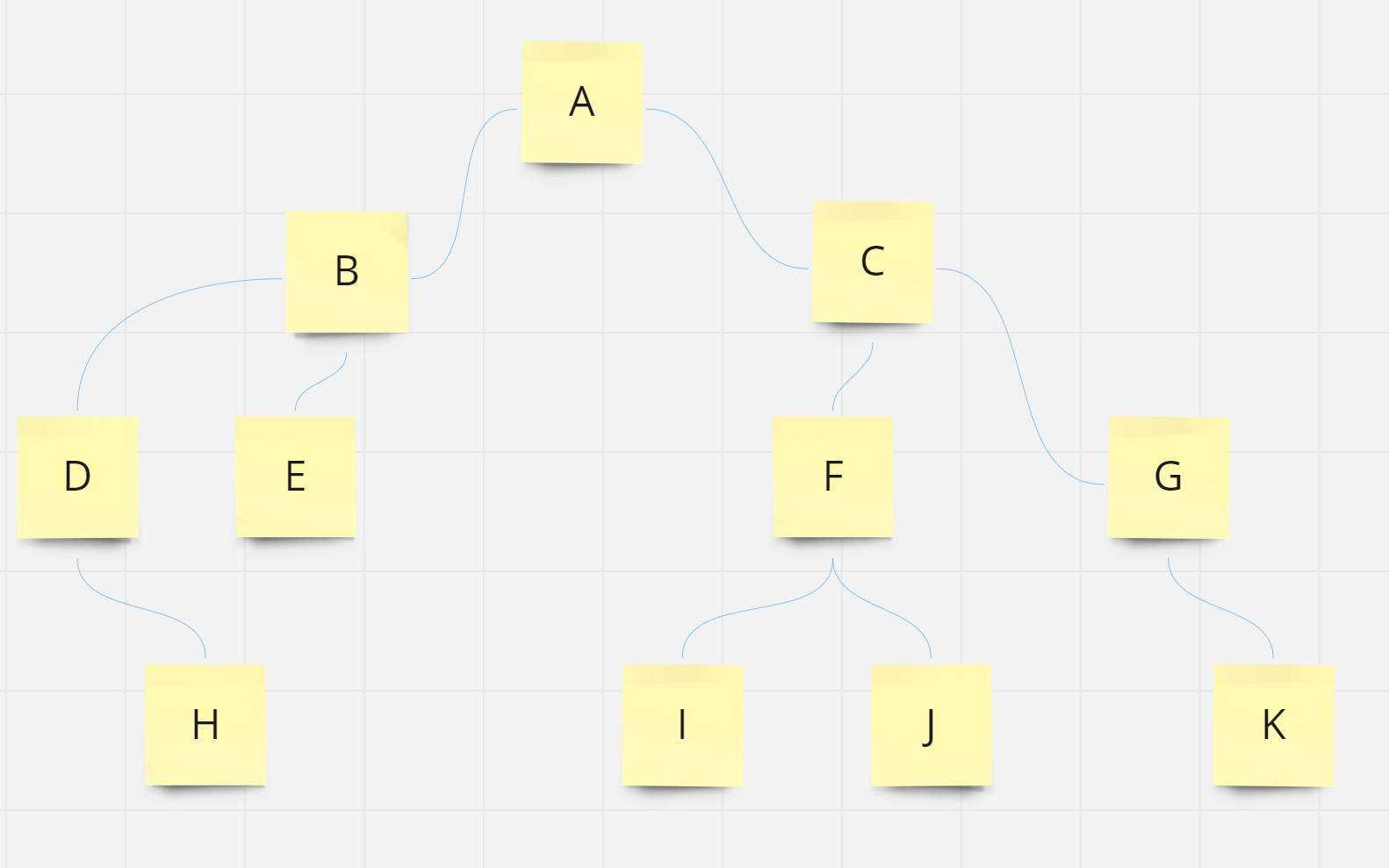 전위탐색, 중위탐색, 후위탐색 순서 예측하기
전위탐색, 중위탐색, 후위탐색 순서 예측하기
- 전위탐색 preorder 정답
- A - B - D - H - E - C - F - I - J - G - K
- 중위탐색 inorder 정답
- D - H - B - E - A - I - F - J - C - G - K
- 후위탐색 postorder 정답
- H - D - E - B - I - J - F - K - G - C - A
js코드로 구현한 이진 트리 탐색
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinaryTree {
constructor() {
this.init();
}
init() {
this.root = null;
}
// 노드를 트리에 삽입하는 메서드
insert(value) {
const newNode = new Node(value);
if (this.root === null) this.root = newNode;
else this._insertRecursive(this.root, newNode);
}
// 노드를 재귀적으로 삽입할 수 있게 도와주는 메서드
_insertRecursive(currentNode, newNode) {
if (newNode.value < currentNode.value) {
if (currentNode.left === null) currentNode.left = newNode;
else this._insertRecursive(currentNode.left, newNode);
} else {
if (currentNode.right === null) currentNode.right = newNode;
else this._insertRecursive(currentNode.right, newNode);
}
}
// 전위 순회 메서드 (루트-왼쪽-오른쪽 순서)
preorderTraversal() {
const result = [];
this._preorderRecursive(this.root, result);
return result;
}
// 전위 순회를 재귀적으로 할 수 있게 도와주는 메서드
_preorderRecursive(currentNode, result) {
if (currentNode !== null) {
result.push(currentNode.value);
this._preorderRecursive(currentNode.left, result);
this._preorderRecursive(currentNode.right, result);
}
}
// 중위 순회 메서드 (왼쪽-루트-오른쪽 순서)
inorderTraversal() {
const result = [];
this._inorderRecursive(this.root, result);
return result;
}
// 중위 순회를 재귀적으로 할 수 있게 도와주는 메서드
_inorderRecursive(currentNode, result) {
if (currentNode !== null) {
this._inorderRecursive(currentNode.left, result);
result.push(currentNode.value);
this._inorderRecursive(currentNode.right, result);
}
}
// 후위 순회 메서드 (왼쪽-오른쪽-루트 순서)
postorderTraversal() {
const result = [];
this._postorderRecursive(this.root, result);
return result;
}
// 후위 순회를 재귀적으로 할 수 있게 도와주는 메서드
_postorderRecursive(currentNode, result) {
if (currentNode !== null) {
this._postorderRecursive(currentNode.left, result);
this._postorderRecursive(currentNode.right, result);
result.push(currentNode.value);
}
}
}이진탐색트리 (Binary Search Tree)
- 트리 구조 자체로는 데이터의 특성에 아무런 제약이 없음
- 어떤 특정한 값을 찾기 위해서는 결국 트리의 모든 데이터를 탐색 해야함
- ex) 데이터 N개가 있을 때 N번 방문해야 함으로 시간복잡도적인 측면에서 이점이 없음 ⇒ O(N)
- 어떤 특정한 값을 찾기 위해서는 결국 트리의 모든 데이터를 탐색 해야함
- 이진탐색트리는 데이터의 특성에 제약을 줌으로 탐색 속도를 바이너르서치처럼 O(logN)으로 줄여줌
특징
- 노드의 왼쪽 서브 트리에는 루트 노드보다 작은 값
- 노드의 오른쪽 서브 트리에는 루트 노드보다 큰 값
- 서브 트리는 다시 이진탐색트리
- 중복된 값은 없음
- 이진트리의 최솟값은 트리의 가장 왼쪽 끝에 위치한 노드가 트리의 최소 값을 가지고 있음 === 1
- 이진트리의 최대값은 트리의 가장 오른쪽 끝에 위치한 노드가 트리의 최대값을 가지고 있음 === 9
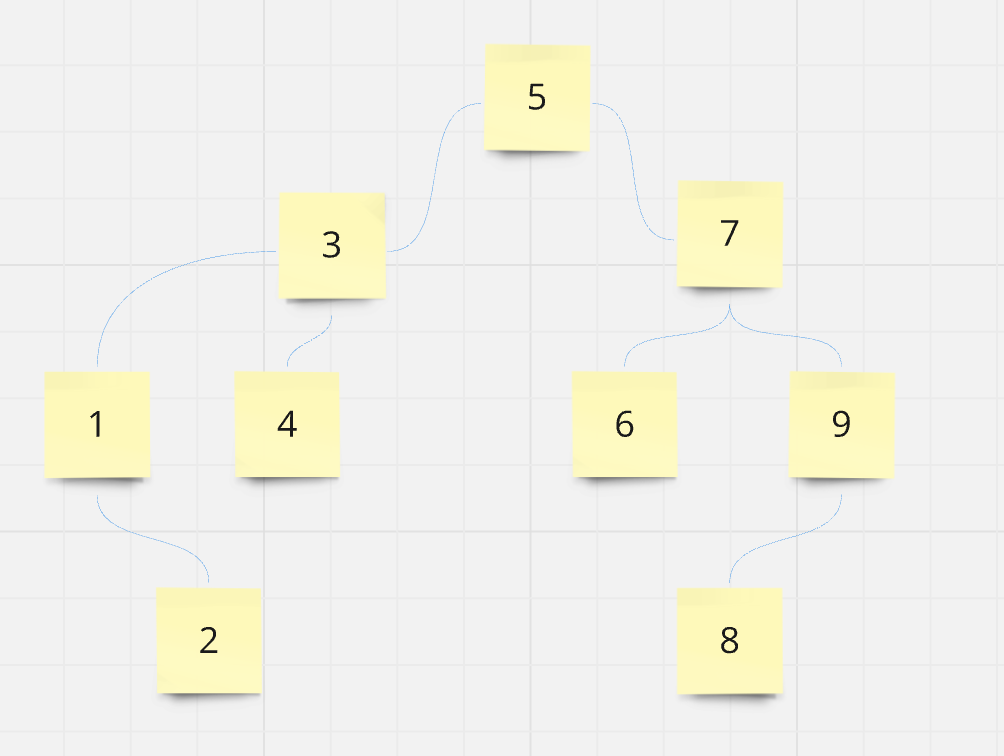 이진탐색트리 예시
이진탐색트리 예시
삽입
- 중복된 데이터는 삽입하지 않음
- 추가된 노드는 트리의 leaf에 삽입
삭제
- 삭제하려는 노드가 자식 노드가 없는 경우
- 해당 노드를 단순히 제거
- 삭제하려는 노드가 하나의 자식 노드만 가진 경우
- 삭제하려는 노드를 제거하고, 그 자식 노드를 삭제된 노드의 위치로 대체
- 삭제하려는 노드가 두 개의 자식 노드를 가진 경우
- 오른쪽 서브트리에서 최소값 노드 찾기: 삭제할 노드의 오른쪽 서브트리에서 가장 작은 값을 가진 노드를 찾기
- 삭제할 노드의 값을 최소값으로 대체: 찾은 최소값을 삭제할 노드의 값으로 대체하고, 최소값 노드를 삭제
js로 구현한 이진탐색트리
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.init();
}
init() {
this.root = null;
}
// 노드를 트리에 삽입하는 메서드
insert(value) {
const newNode = new Node(value);
if (this.root === null) this.root = newNode;
else this._insertRecursive(this.root, newNode);
}
// 노드를 재귀적으로 삽입할 수 있게 도와주는 메서드
_insertRecursive(currentNode, newNode) {
if (newNode.value < currentNode.value) {
if (currentNode.left === null) currentNode.left = newNode;
else this._insertRecursive(currentNode.left, newNode);
} else {
if (currentNode.right === null) currentNode.right = newNode;
else this._insertRecursive(currentNode.right, newNode);
}
}
// 트리에서 노드를 삭제하는 메서드
delete(value) {
this.root = this._deleteRecursive(this.root, value);
}
// 노드를 재귀적으로 삭제할 수 있게 도와주는 메서드
_deleteRecursive(currentNode, value) {
if (currentNode === null) return null;
if (value < currentNode.value)
currentNode.left = this._deleteRecursive(currentNode.left, value);
else if (value > currentNode.value)
currentNode.right = this._deleteRecursive(currentNode.right, value);
else {
// 삭제할 노드를 찾았을 때
if (currentNode.left === null) return currentNode.right;
else if (currentNode.right === null) return currentNode.left;
// 두 자식이 있는 경우, 오른쪽 서브트리에서 최소값을 찾아 대체
currentNode.value = this._findMinValue(currentNode.right);
currentNode.right = this._deleteRecursive(
currentNode.right,
currentNode.value,
);
}
return currentNode;
}
// 오른쪽 서브트리에서 최소값을 찾는 메서드
_findMinValue(node) {
let current = node;
while (current.left !== null) {
current = current.left;
}
return current.value;
}
// 트리에서 특정 값을 검색하는 메서드
search(value) {
return this._searchRecursive(this.root, value);
}
// 값을 재귀적으로 검색할 수 있게 도와주는 메서드
_searchRecursive(currentNode, value) {
if (currentNode === null) return false;
if (value === currentNode.value) return true;
else if (value < currentNode.value)
return this._searchRecursive(currentNode.left, value);
// 왼쪽 서브트리 탐색
else return this._searchRecursive(currentNode.right, value); // 오른쪽 서브트리 탐색
}
}
