다익스트라 알고리즘

다익스트라 알고리즘은 그래프에서 한 정점부터 다른 모든 정점까지의 최단 경로를 찾는 알고리즘이다.

우리 일상생활에서 해당 알고리즘 사용 예시는 내비게이션 시스템, 네트워크 라우팅, 항공 노선 계획 등이있다

• 내비게이션 시스템 :
  • 가장 흔한 예시입니다. 차량용 GPS나 스마트폰 지도 앱에서 최단 경로를 찾을 때 사용됩니다.
• 네트워크 라우팅 :
  • 인터넷에서 데이터 패킷이 가장 효율적인 경로로 전송되도록 하는 데 사용됩니다.
  • 라우터들 사이의 최적 경로를 결정하여 네트워크 트래픽을 관리합니다.
• 항공 노선 계획:
  • 항공사들이 비행 경로를 최적화할 때 사용합니다.
  • 연료 비용, 비행 시간, 공항 사용료 등을 고려하여 최적의 경로를 찾습니다.

특징

• 양의 가중치를 가진 방향 그래프에서 작동합니다. ⇒ 음수인 가중치를 가진 간선은 포함될 수 없다
  • 다익스트라 알고리즘은 한 번 처리한 노드를 다시 방문하지 않는다는 가정 하에 작동합니다.
    
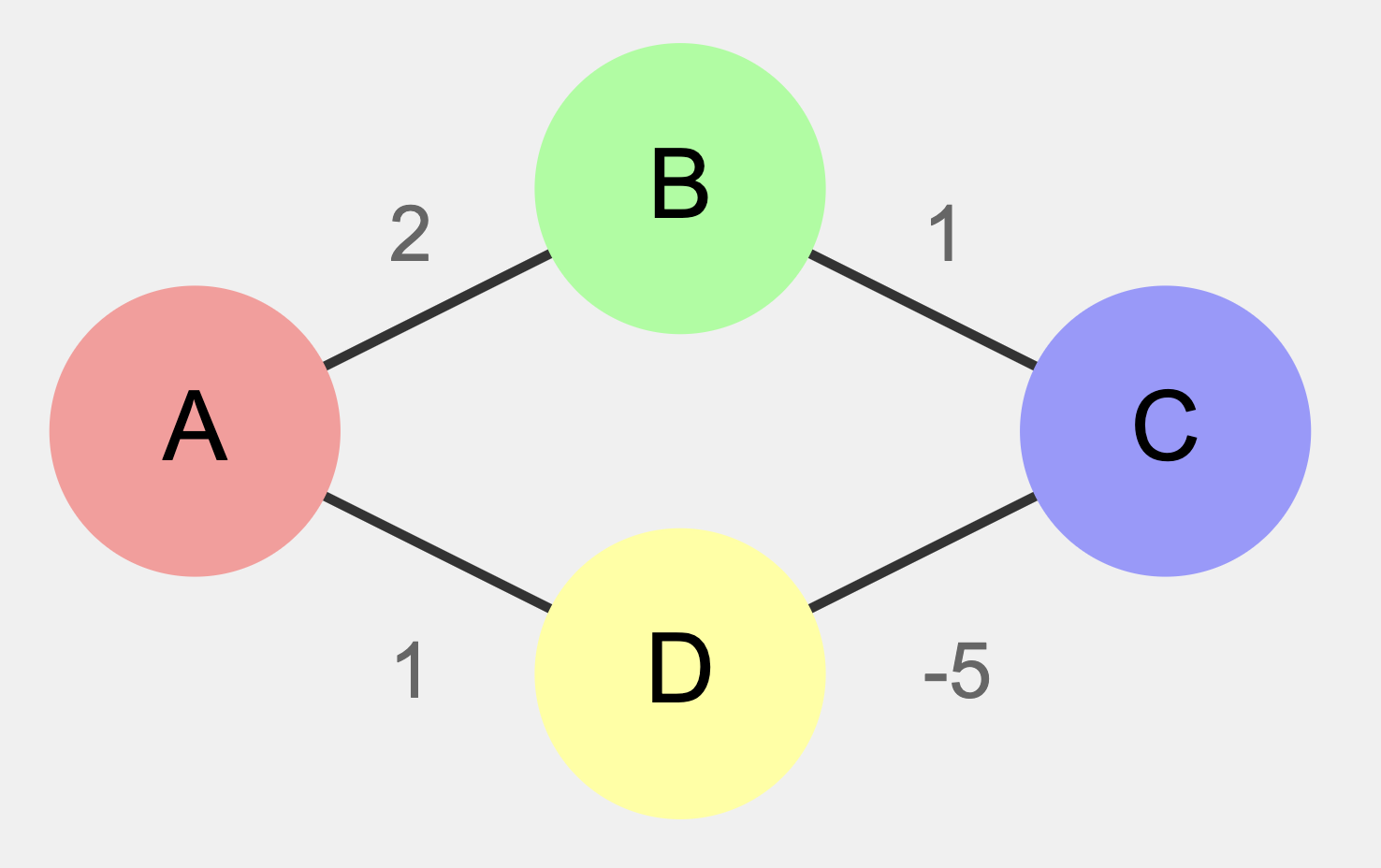
  • 위 사이클을 무한히 반복할수록 경로의 총 가중치는 계속해서 감소합니다.
  • 다익스트라 알고리즘은 이 사이클을 무한히 반복하며 계속해서 더 짧은 경로를 찾으려 할 것이고 결국 문한루프에 빠지게 됩니다
• 시작 정점에서 도착 정점까지의 모든 가중치를 계산하고 최단 거리를 찾습니다

진행 과정

• 초기화 :
  • 시작 정점의 거리를 0으로 설정합니다.
  • 다른 모든 정점의 거리를 무한대로 설정합니다.
  • 방문하지 않은 정점들의 테이블을 만듭니다.
• 반복 :
  • 방문하지 않은 정점 중 현재 알려진 거리가 가장 짧은 정점을 선택합니다.
  • 선택한 정점을 방문한 것으로 표시합니다.
  • 선택한 정점의 인접 정점들에 대해 :
    • 시작점에서 현재 정점을 거쳐 인접 정점으로 가는 거리를 계산합니다.
    • 이 거리가 기존에 알려진 거리보다 짧다면 업데이트합니다.
• 종료 :
  • 모든 정점을 방문할 때까지 b 단계를 반복합니다.

작동 예시

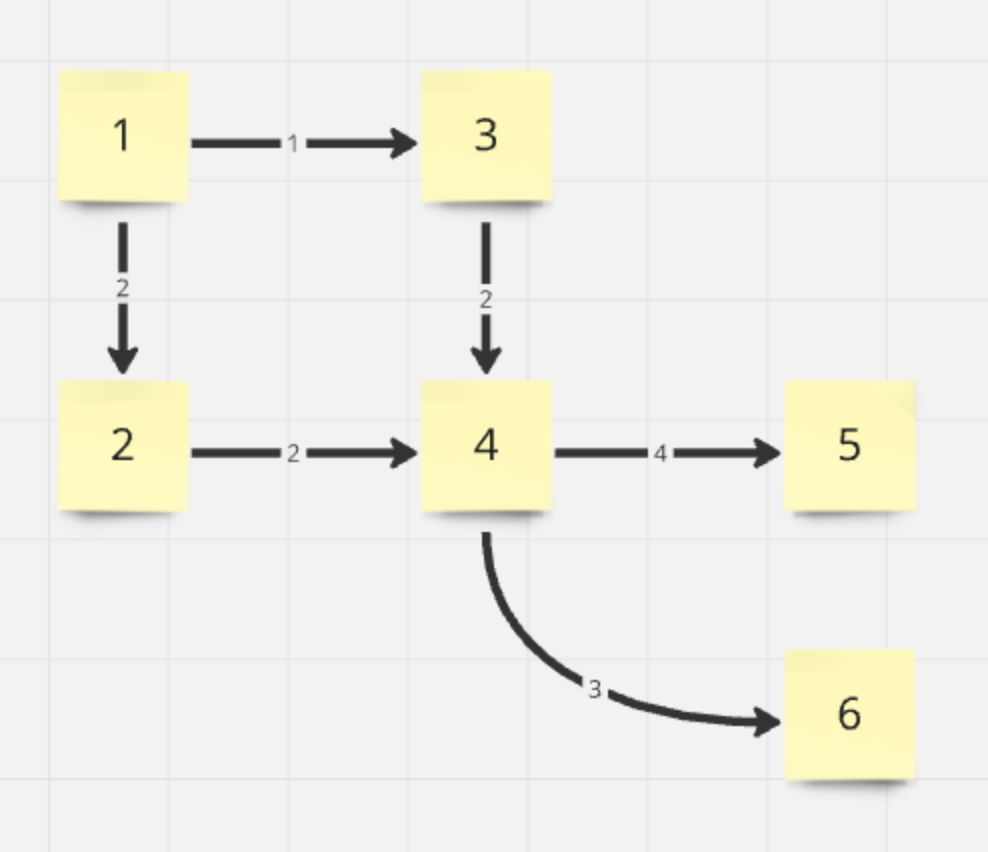
노드	1	2	3	4	5	6
거리	Inf	Inf	Inf	Inf	Inf	Inf
방문	false	false	false	false	false	false

---

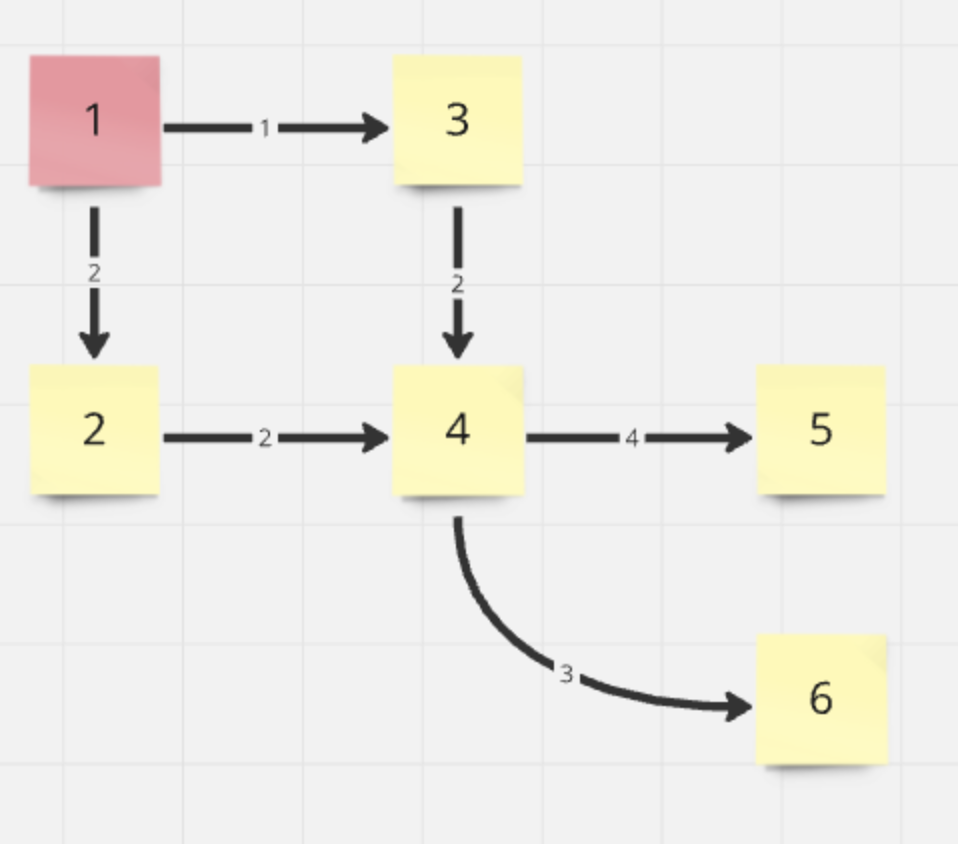
노드	1	2	3	4	5	6
거리	0	Inf	Inf	Inf	Inf	Inf
방문	true	false	false	false	false	false

---

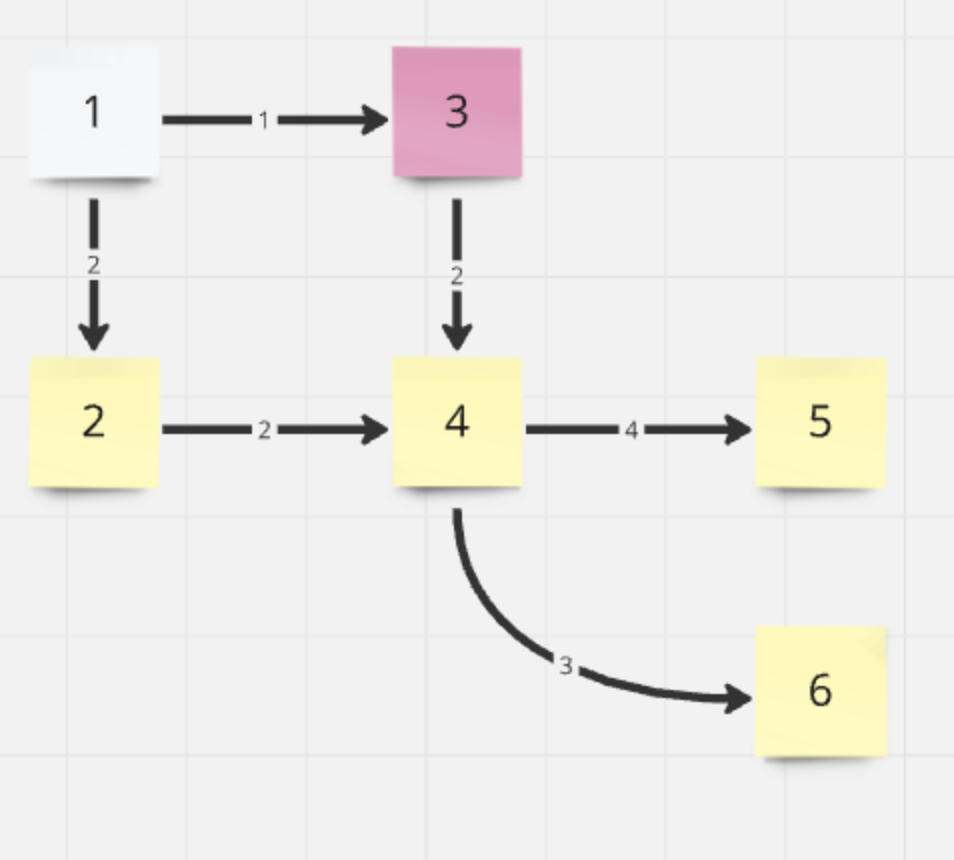
노드	1	2	3	4	5	6
거리	0	2	1	Inf	Inf	Inf
방문	true	false	true	false	false	false

---

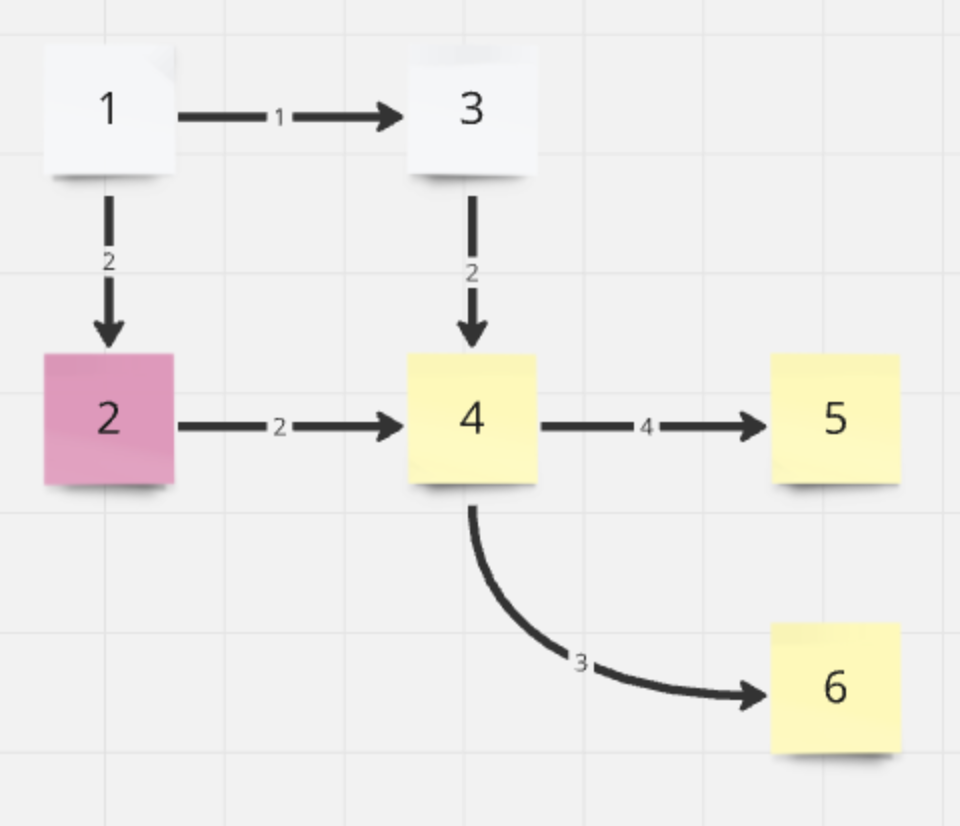
노드	1	2	3	4	5	6
거리	0	2	1	3	Inf	Inf
방문	true	true	true	false	false	false

---

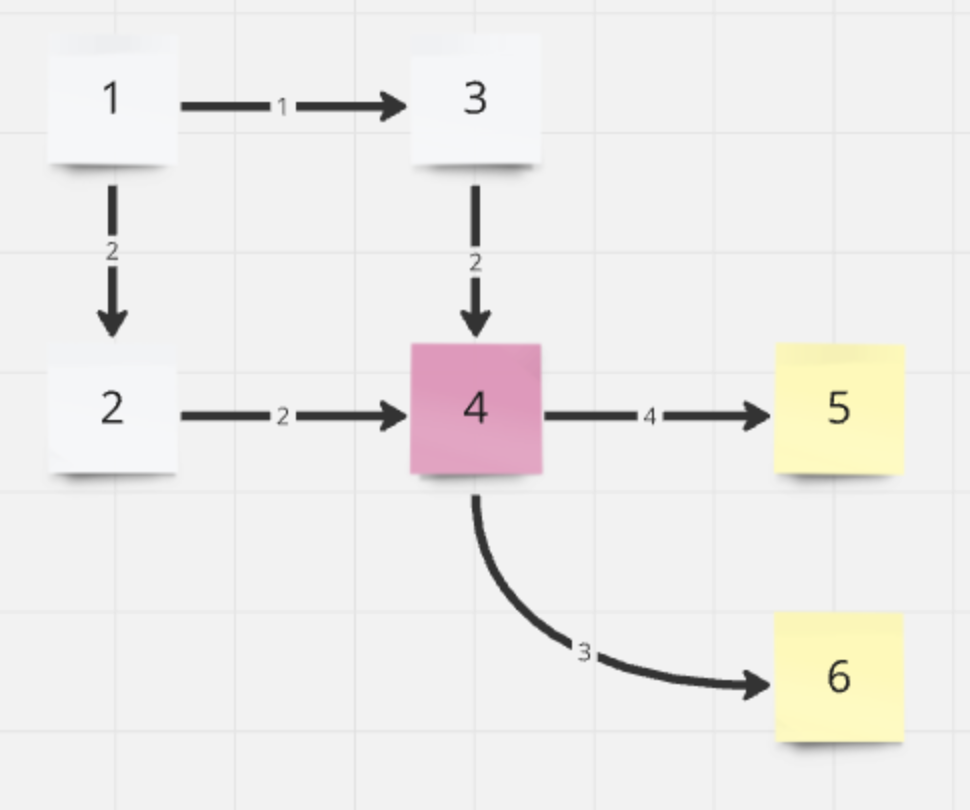
노드	1	2	3	4	5	6
거리	0	2	1	3	7	6
방문	true	true	true	true	false	false

---

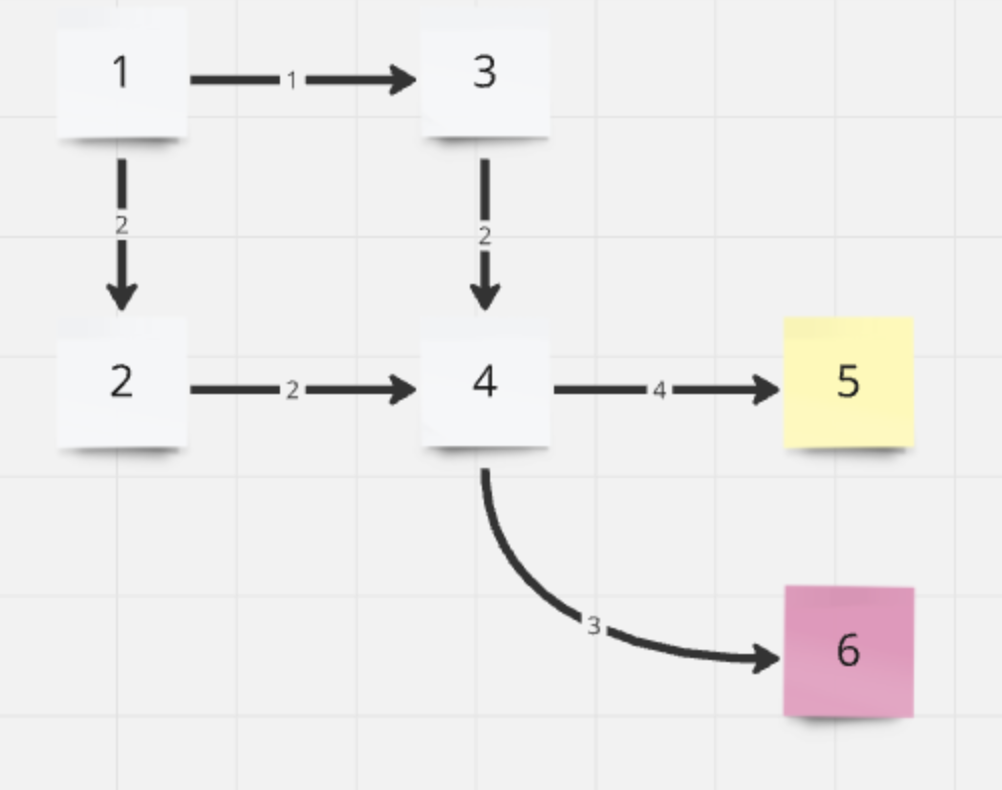
노드	1	2	3	4	5	6
거리	0	2	1	3	7	6
방문	true	true	true	true	false	true

---

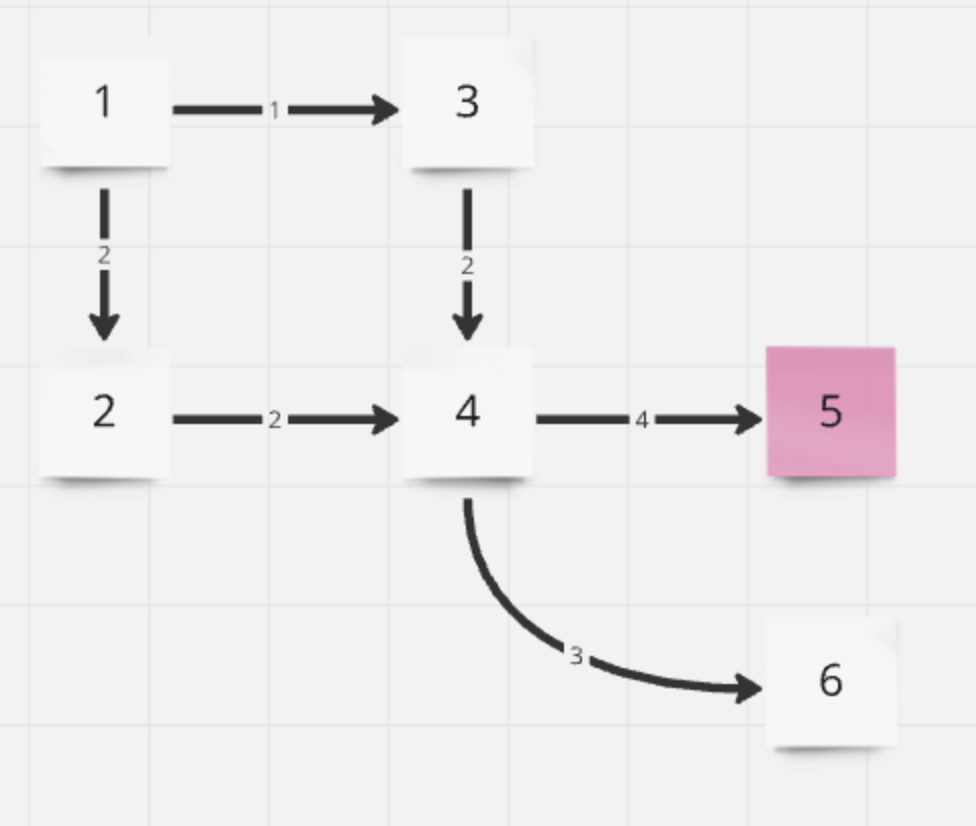
노드	1	2	3	4	5	6
거리	0	2	1	3	7	6
방문	true	true	true	true	true	true

---

JS로 구현한 다익스트라

function dijkstra(graph, start) {
  const n = graph.length;
  const distances = new Array(n).fill(Infinity);
  const visited = new Array(n).fill(false);
  distances[start] = 0;

  for (let i = 0; i < n; i++) {
    // 방문하지 않은 노드 중 가장 가까운 노드를 찾습니다
    let minDistance = Infinity;
    let minIndex = -1;
    for (let j = 0; j < n; j++) {
      if (!visited[j] && distances[j] < minDistance) {
        minDistance = distances[j];
        minIndex = j;
      }
    }

    // 모든 노드를 방문했거나 연결되지 않은 노드만 남은 경우
    if (minIndex === -1) break;

    visited[minIndex] = true;

    // 선택된 노드를 거쳐 다른 노드로 가는 거리를 계산합니다
    for (let [neighbor, weight] of graph[minIndex]) {
      const newDistance = distances[minIndex] + weight;
      if (newDistance < distances[neighbor]) {
        distances[neighbor] = newDistance;
      }
    }
  }

  return distances;
}

// 주어진 그래프
const graph = [
  [[1, 5], [3, 1]],
  [[0, 5], [2, 1], [4, 3]],
  [[1, 1], [3, 2], [5, 2], [6, 8]],
  [[0, 1], [2, 2], [5, 1]],
  [[1, 3], [6, 1]],
  [[2, 2], [3, 1], [6, 3]],
  [[2, 8], [4, 1], [5, 3]],
];

// 시작 노드 (0번 노드에서 시작)
const startNode = 0;

// 알고리즘 실행
const shortestDistances = dijkstra(graph, startNode);

console.log(`노드 ${startNode}에서 각 노드까지의 최단 거리:`);
shortestDistances.forEach((distance, node) => {
  console.log(`${startNode} → ${node}: ${distance}`);
});