1. WHY 통계?

1-1. 평균 구해보소

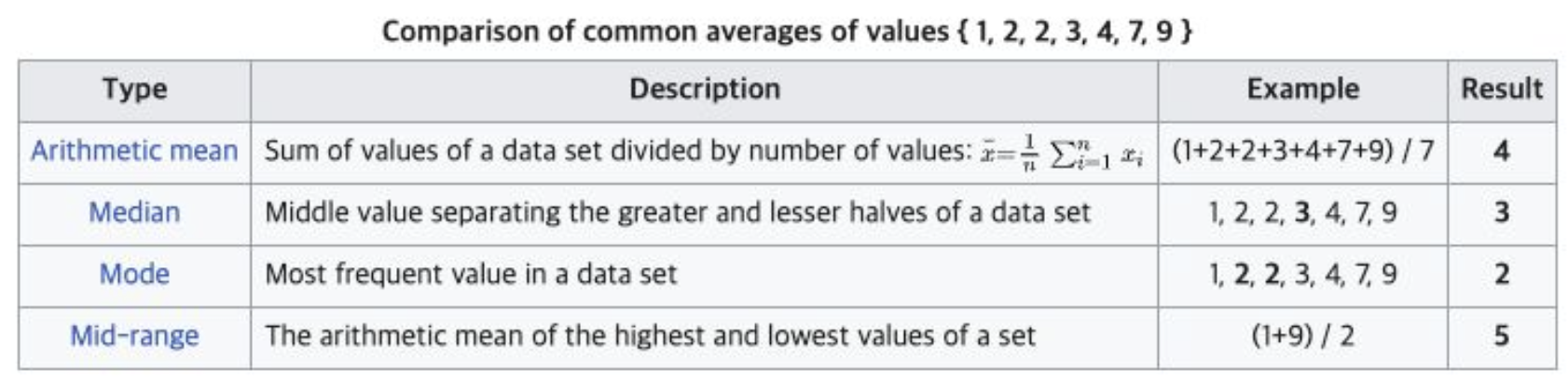
종류 겁나게 많음. 상황에 맞게 적절히 잘 고르는 것이 중요

1.2 불확실성을 다루는 통계

2. 확률

2-1. 확률이란?

• 확률 분포란 확률 변수가 특정한 값을 가질 확률을 나타내는 함수
• 확률 변수는 확률적으로 값이 결정되는 변수
• 확률분포는 확률변수가 어떤 값일 확률을 나타내는함수
• 확률은 어떤 사건이 일어났을지에 대한 가능성을 0~1사이의 숫자로 표현한 값

2-2. pmf vs pdf

<PMF: Probability Mass Function>

확률 변수가 이산적인(discrete) 값을 가질 때 사용. 이산 확률 변수는 유한한 개수의 가능한 값 중 하나를 . PMF는 각 가능한 값에 대한 확률을 제공. 이러한 확률을 질량으로 생각할 수 있으며, 각 값에 할당된 확률을 질량으로 나타냄.

확률 변수가 이산 확률 변수인 경우 PMF 표현:

• P(X = x) = 확률 변수 X가 값 x를 가질 확률

• EX) 동전 던지기에서 앞면과 뒷면의 나올 확률은 PMF로 표현. P(X = 앞면) = 0.5, P(X = 뒷면) = 0.5와 같이 표현

<PDF: Probability Density Function>
확률 변수가 연속적인(continuous) 값을 가질 때 사용. 연속 확률 변수는 무한한 범위 내에서 어떤 값이든 가짐. PDF는 확률 변수의 가능한 값 범위에서 확률을 나타냄. PDF 값은 확률이 아닌 확률 밀도로 해석, 어떤 구간 내에서 확률을 계산하기 위해 해당 구간 아래의 PDF 곡선 아래의 면적을 계산.

확률 변수 X의 PDF를 f(x)로 표현할 때, 다음과 같이 적분을 사용하여 확률을 계산할 수 있습니다:

• P(a ≤ X ≤ b) = ∫(from a to b) f(x) dx

• EX)정규 분포의 PDF는 종 모양 곡선으로 표현되며, 특정 구간 내의 확률은 해당 구간 아래의 PDF 곡선 아래의 면적으로 계산

요약하면, PMF는 이산 확률 변수에 대한 확률을 나타내고, PDF는 연속 확률 변수에 대한 확률을 나타냄. PMF는 확률을 질량으로 나타내고, PDF는 확률을 밀도로 나타냄.

3. 분포

3-1. pmfs

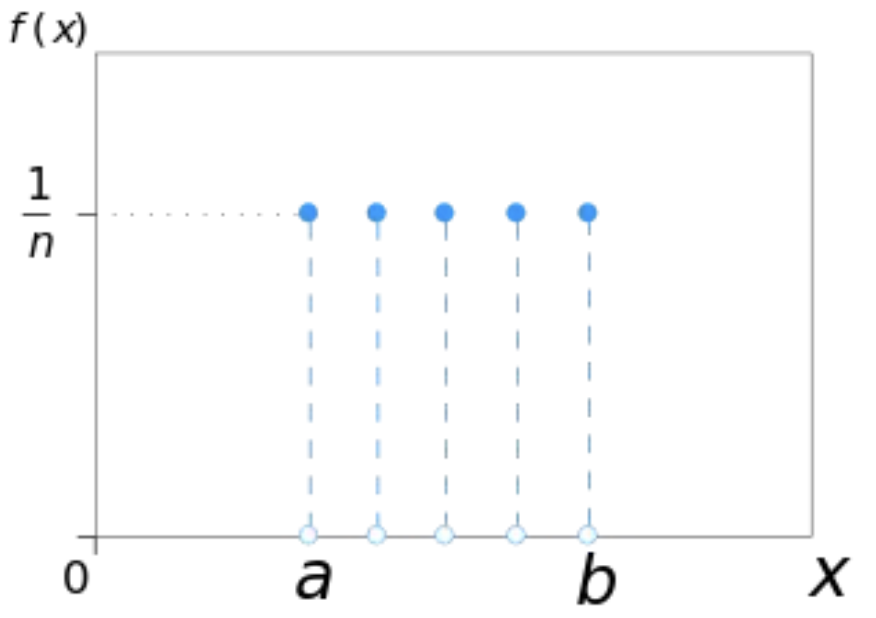
3-1-1. 균일분포(Uniform Distribution)

• 가장 쉬운 분포 ex) 주사위
• a,b 2개의 모수 존재: n= b-a+1 (a는 minimum, b는 maximum)
  

3-1-2. 베르누이 분포(Bernoulli Distribution)

• 두 번째로 쉬운 분포
• True / False처럼 두 가지 중 하나만 가능한 것 ex) 동전
• 확률 p라는 하나의 모수만이 존재
• 쉬워보이지만, logistic regression에 적용

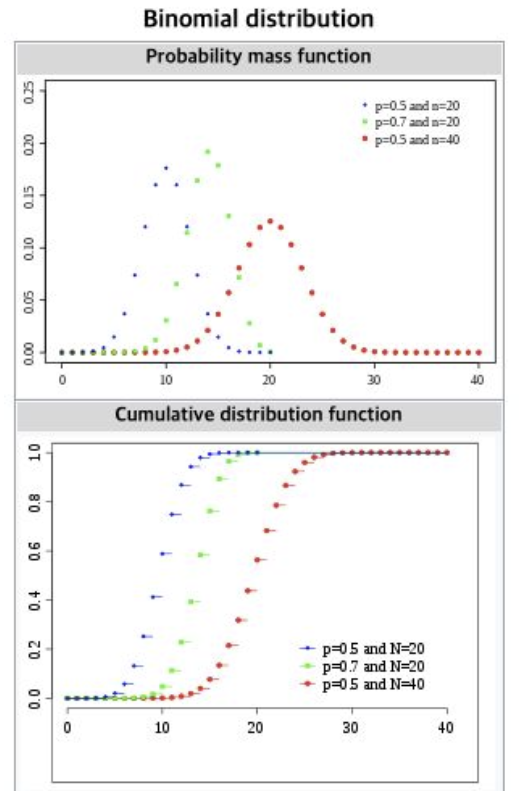
3-1-3. 이항분포(Binomial Distribution)

• 다수의 베르누이 합친 것 ex) 동전 10개 던져서 앞면이 나온 수
• 모수로 확률 P, 시행횟수 n 존재
• 가장 많이 쓰이는 분포 중 하나
  

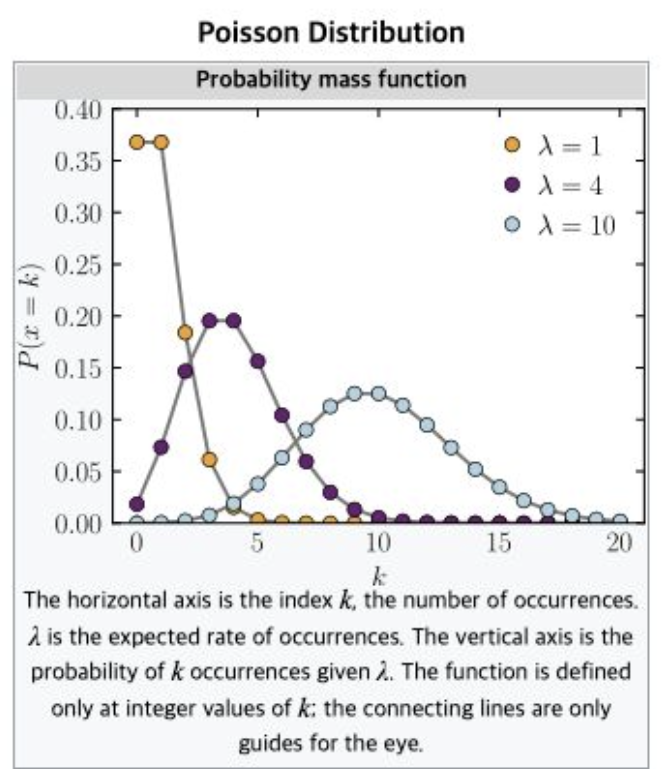
3-1-4. 포아송분포(Poisson Distribution)

• "발생횟수"로 이해하자 ex) 1시간 안에 들어오는 트래픽 수
• 모수가 평균 하나인 독특한 분포
  

3-2. pdfs

3-2-1. 균일 분포(Uniform Distribution)

• pmf와 pdf에 모두 존재

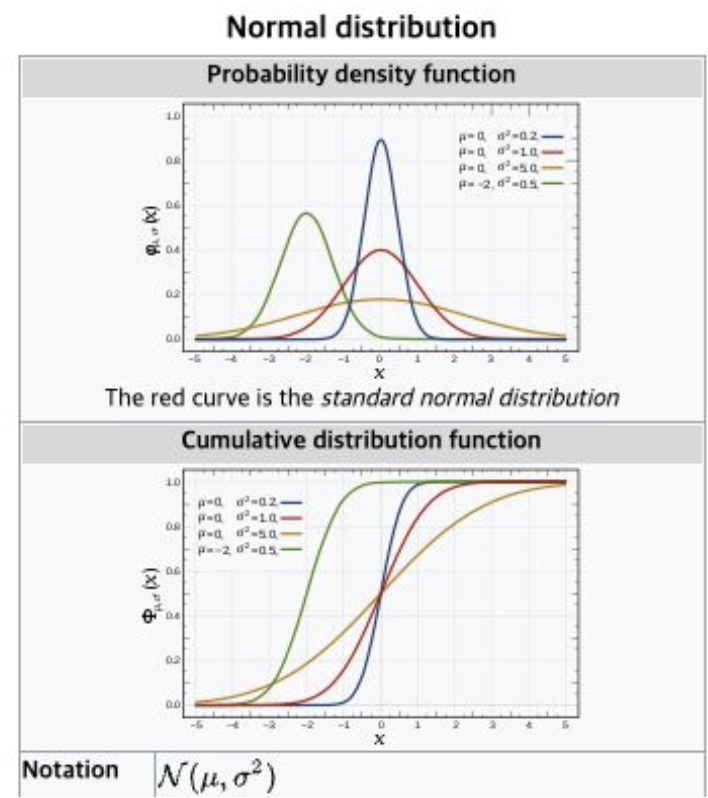
3-2-2. 정규분포(Normal Distribution)

가장 많이 언급/활용되는 분포

• 평균과 분산, 두 개의 모수가 존재
• 좌우 대칭이라는 특징
• 종모양으로 많이 언급
• 평균=0, 분산=1인 정규분포를 특별히 표준정규분포라 칭함.
• 임의의 정규분포는 변환(Transformation)을 통해 표준정규분포로 변환 가능합니다
• z라고 줄여서 부르기도 합니다
• Guassian 분포라고도 부름
  

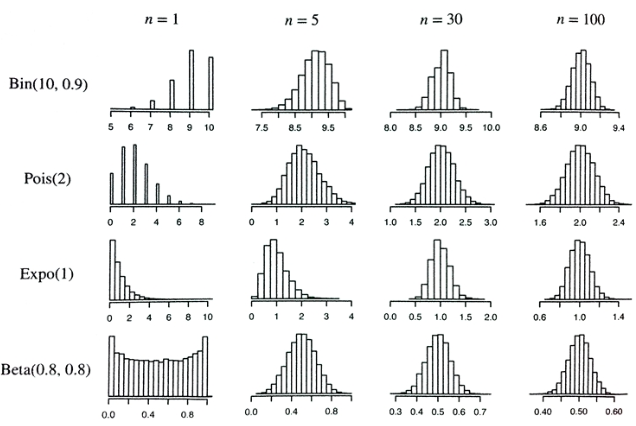
3-2-3. 중심극한정리(Central Limit Theorem,CLT)

• 정규분포가 가장 많이 언급되는 이유 중 하나
• 임의의 분포에서 실현된 n개의 데이터가 있을 때 산술평균은 n이 커짐에 따라 정규분포로 수렴.
• n의 기준을 30으로 많이 제안하나, 꼭 그렇진 않음.( t분포와 관련된 숫자들을 한 페이지에 담기 위함이라 추정됨)
• 현실적으로 skew와 outlier의 문제로 수렴이 어려울 수 있음.
  

3-2-4. Sigma

분산과 표준편차 중 뭘 많이 쓸까? --- 표준편차

• 표준편차를 흔히 sigma라고 부름
• 표준정규분포에서는, 시그마를 통해 해당 값이 얼마나 특이한지 쉽게 계산 가능

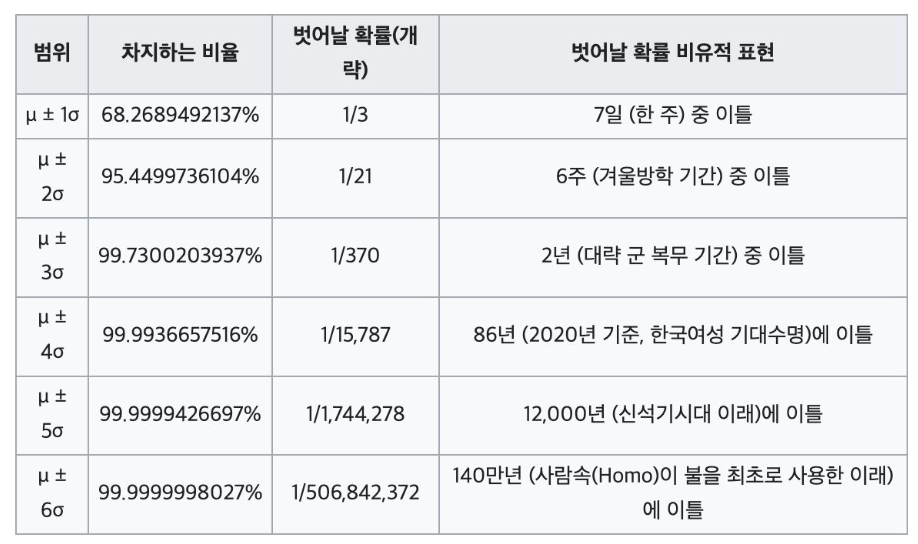
3-2-5. student's t분포

(모분산을 모르는 상태에서 평균 추정, p-value도출 0.05이하이면 두 집단 간 평균 차이가 유의미 == 귀무가설 기각: ~하지 않을 것이다에 대한 반론의 근거)

정규 분포와 유사하며, 박빙으로 많이 쓰이는 분포

• 평균과 자유도, 두 개의 개념이 존재
• 자유도는 데이터의 수 즉 변수의 갯수, t-분포는 정규 분포를 따르는 확률 변수들의 표본 평균을 계산할 때 사용. 자유도는 표본 평균을 계산할 때 사용한 표본의 크기를 나타냄.(자유도 높을 수록 t분포가 정규분포를 따름)
• 정규 분포를 이용해 평균을 추정할 때, 분산을 사용하는데
• 모분산을 모르는 상태에서 둘을 동시에 추정하기 어렵기 때문에
• 이를 대신하기 위해 t 분포 사용
• 종종 n=30을 기준으로 z/t 검정을 분리하는데
• 그냥 항상 t-test쓰자(데싸들이 그렇다고 한다)
• n이 충분히 크면 두 검정 사이에 차이도 안난다.!
  

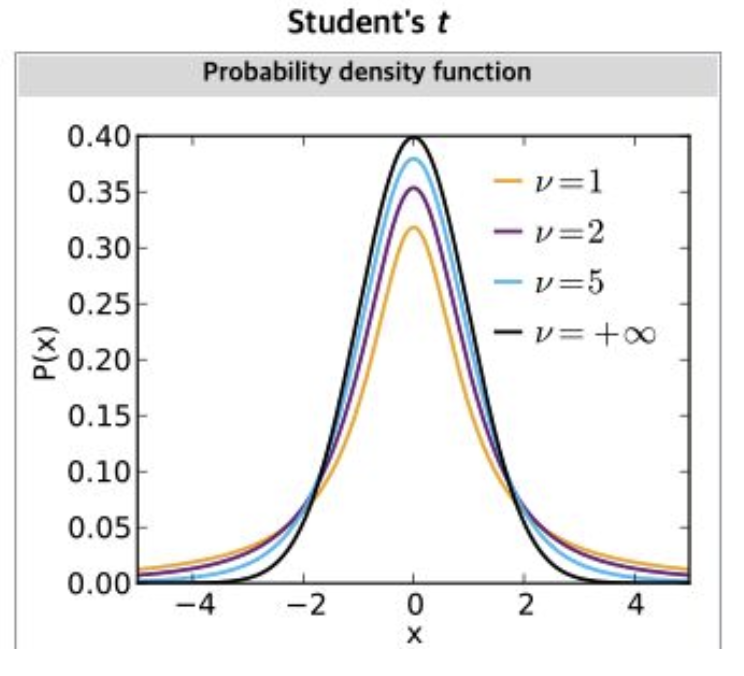
3-2-6. F분포

두 개의 분산 또는 변동성을 비교하거나 검정하는 데 주로 활용. F-분포는 일반적으로 두 모집단의 분산을 비교하고, 회귀 분석 모델의 적합도를 평가하는 데 사용함.

• 두 카이제곱 분포의 ratio로 정의되는 분포
• 각 카이제곱 분포의 각각의 자유도 2개가 모수
• 분산의 비ratio에 대한 분포(카이제곱과 다르게 집단 간의 분포 다룸)

주요 사용 사례:
-분산 비교: F-분포는 두 개의 모집단 또는 그룹의 분산을 비교하는 데 사용. 두 그룹 간의 분산 비율을 비교하여 통계적으로 유의미한 차이를 확인가능. 이런 경우에 분산 비율 F-검정(ANOVA, Analysis of Variance)이라고도함.
-회귀 분석: 회귀 분석에서 F-분포는 모델의 적합도를 평가하는 데 사용. 회귀 모델의 적합도를 확인하거나 모델 간의 차이를 비교할 때 사용.

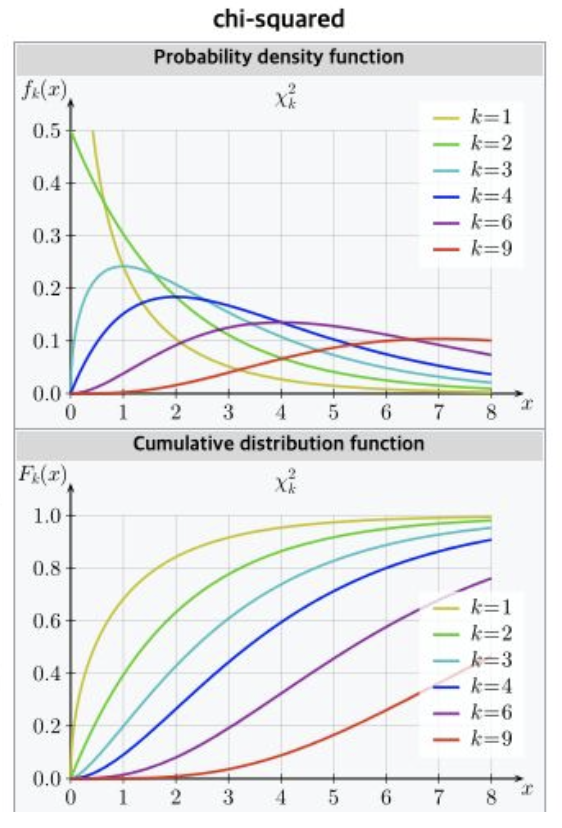
3-2-7. 카이제곱 분포

• 오차와 분산과 관련된 분포라고, 직관적으로 받아들이자(분산의 분포를 확률분포로 나타낸 것)
• k개의 표준정규분포를 제곱하여 합하면 나오는 분포
• 표준정규분포는 평균이 0, k를 곱하면 그대로 분산
• 모수는 k하나, 이를 자유도라고 함.

주요 사용 사례:

• 분산 추정: 카이제곱 분포는 모집단의 분산을 추정할 때 사용. 분산을 추정하는데 사용되는 표본 분산은 카이제곱 분포를 따름.
• 가설 검정: 카이제곱 분포는 독립성 검정, 적합도 검정, 분포 차이 검정 등과 관련된 가설 검정에 사용. 특히, 카이제곱 검정(Chi-Square Test)은 범주형 데이터의 독립성을 검정하는 데 주로 활용.