가중치 초기화
why?
- 가중치 초기화(Weight Initialization)를 진행하지 않으면 모델의 층이 깊어질수록 활성화 함수 이후 데이터의 분포가 한 쪽으로 쏠릴 수 있다. 이러한 현상은 효율적이고 원활한 모델 학습을 방해한다.
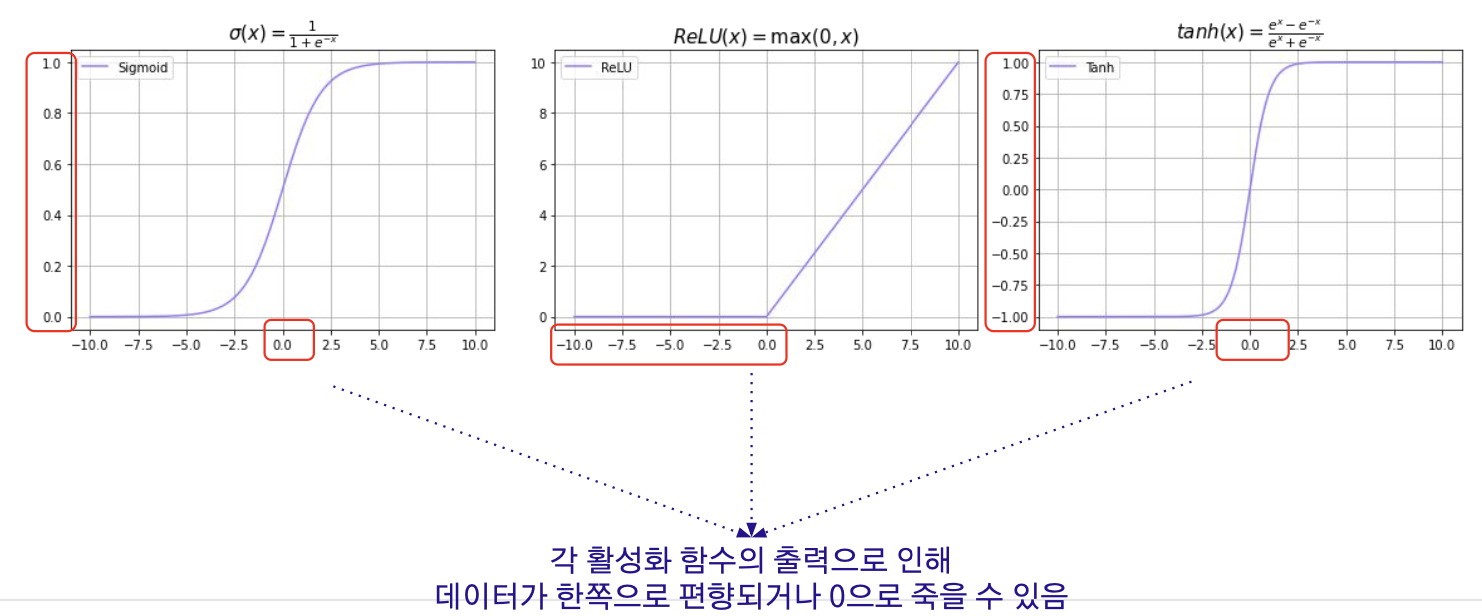
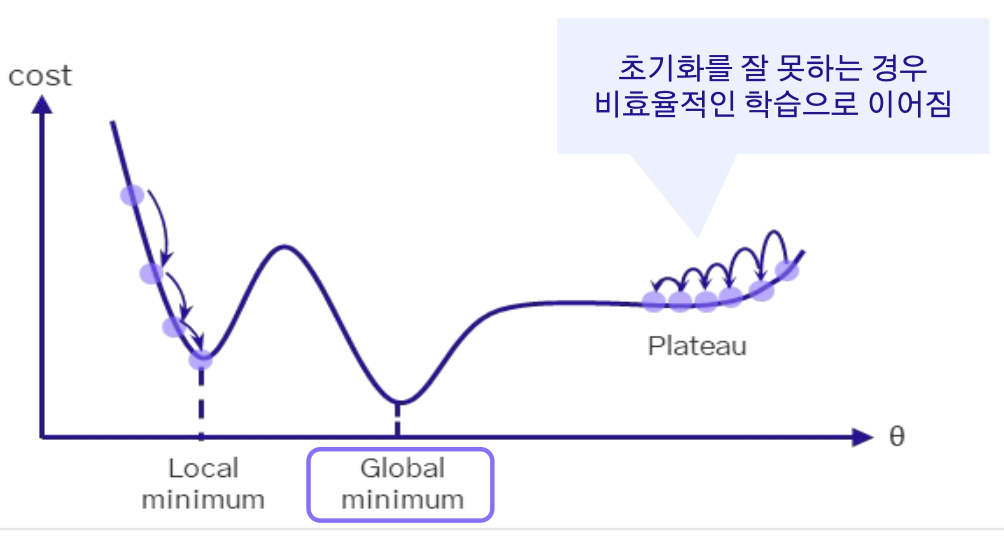
- 전역 최소값을 나아가는 과정에서 가장 중요한 부분이기도 하다. Plateau와 같은 지점에서 초기화가 된다면 모델 학습이 비효율적으로 이뤄질 수 있다.
- 모델의 층이 깊어질수록 손실 함수로부터의 기울기 값이 점점 작아지거나 커질 수 있다.
이러한 현상은 오차역전파로 가중치를 갱신해야하는 모델의 학습을 효율적으로 진행되지 않게 만들 수 있다.
How?
모두 0으로 초기화?
0으로 초기화하면 손실함수로부터의 기울기가 있어도 업데이트 불가
(최악의 말도 안되는 방법)
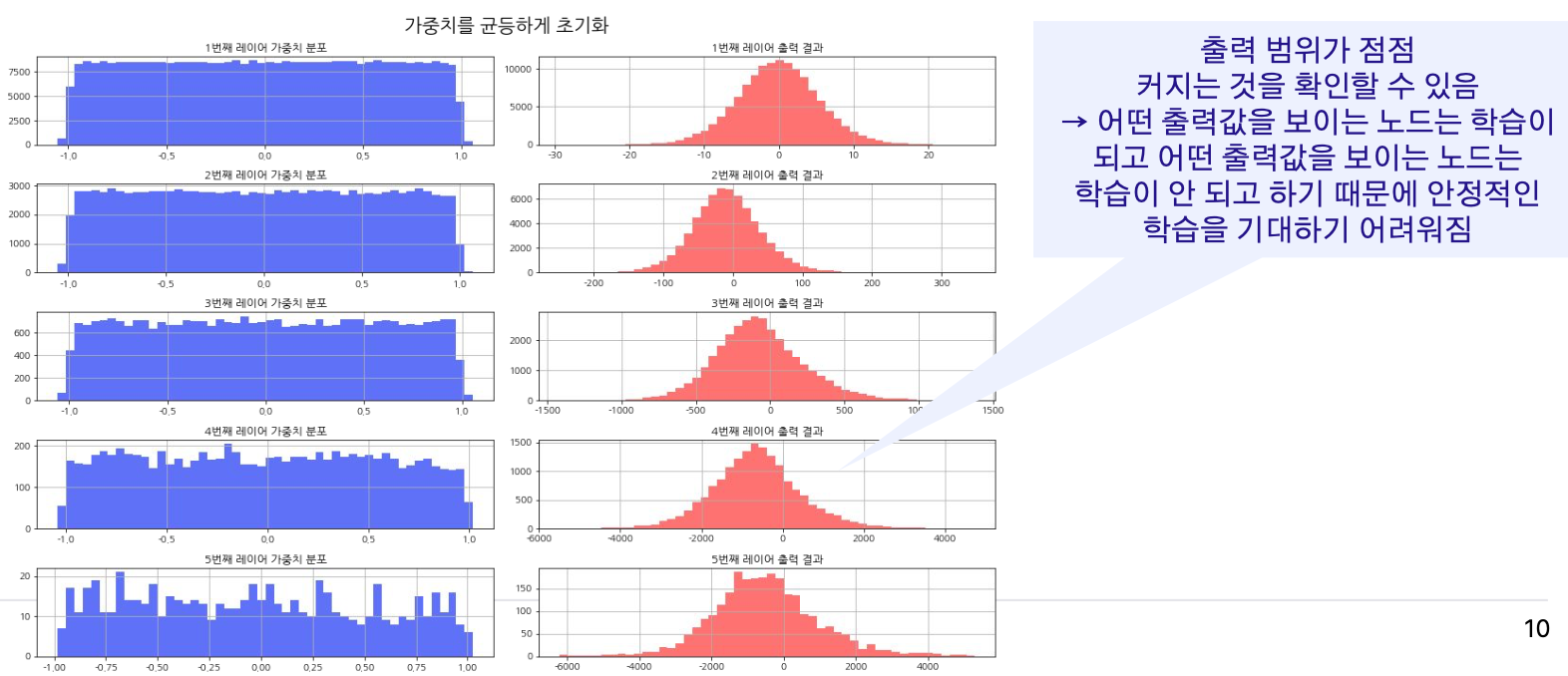
균등하게 초기화?
출력의 범위가 너무 넓어짐
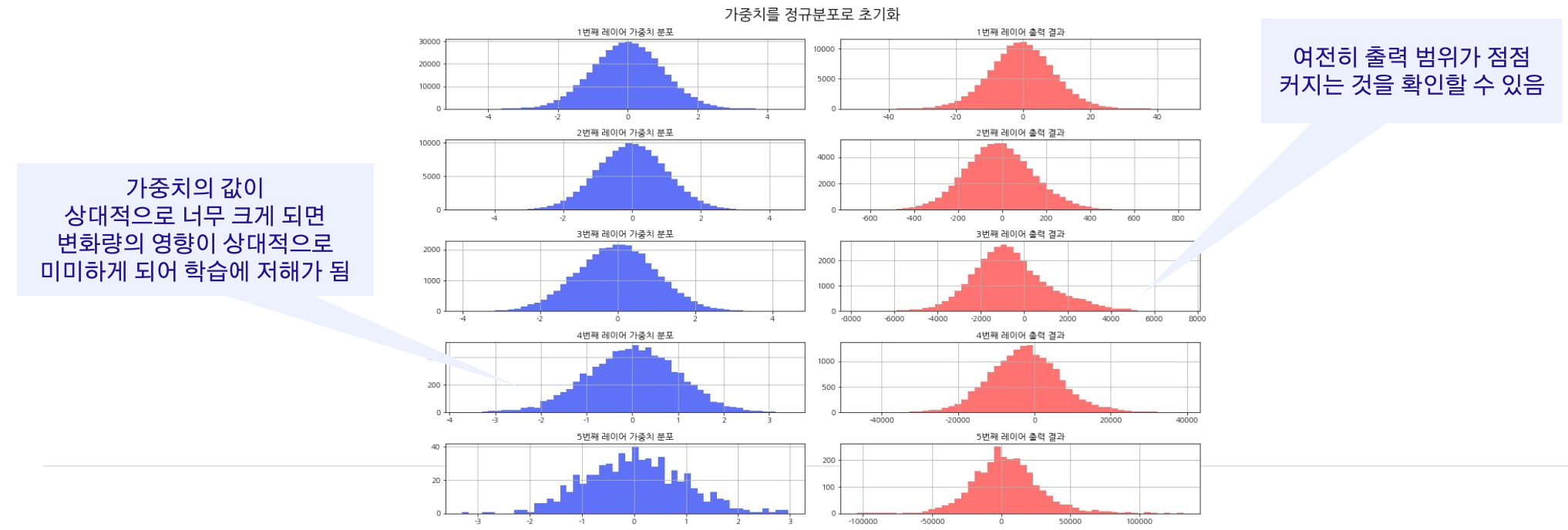
표준 정규분포로 초기화?
가중치의 값이 너무 크거나 너무 작게 초기화되어 학습에 방해
그럼 어쩌라고?
핵심: 각 층의 활성화 함수 이후 출력값이 적당히 넓게 고루 분포되어야함. 그래야 학습 시 편향되지 않고 효율적으로 이뤄짐(Xavier, He)
Xavier
sigmoid나 hypublic tanh 같은 선형 활성화 함수 or 이들의 근사를 사용할 때 효과적. (초기에 너무 큰 가중치 값을 설정하면 기울기가 너무 커지거나 작아져서 학습이 어렵게 될 수 있는 문제 해결가능 + 이전 레이어의 노드 수에 비례하여 가중치를 초기화 -> 이를 통해 이전 레이어의 노드 수가 많을수록 각 가중치의 크기는 작아지게됨)
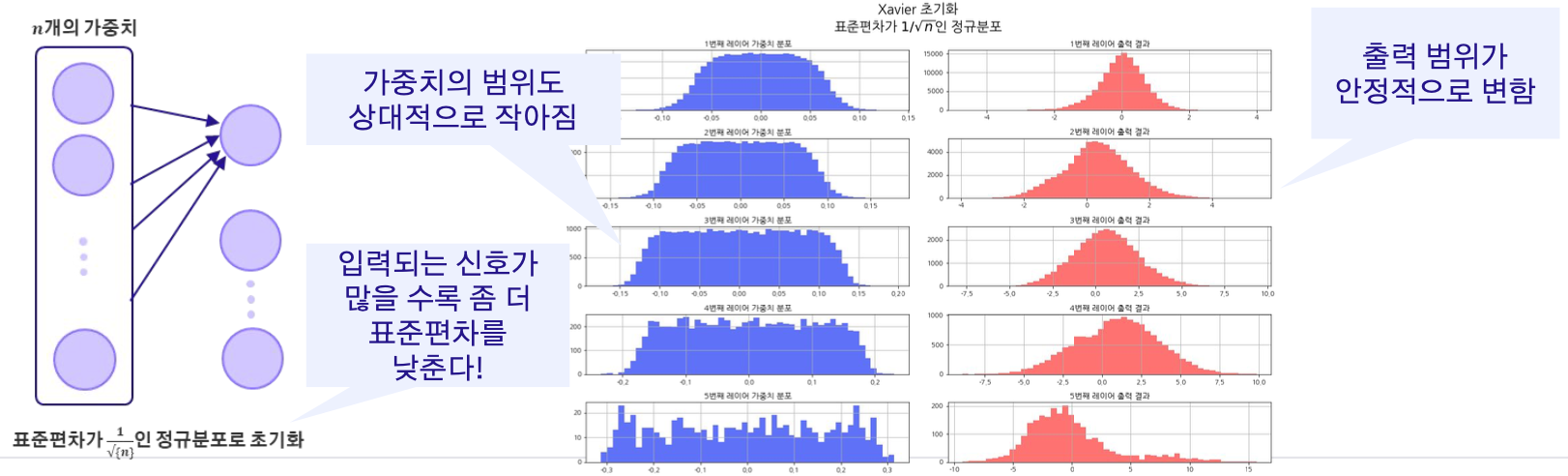
시그모이드와 같은 활성화 함수에선 효과가 좋았지만, 특정한 활성화 함수에선 여전히 문제를 해결할 수 없었다. 예를 들면, ReLU 활성화 함수의 미분값은 음수일 때 출력이 0이므로, 여전히 레이어가 깊어질수록 기울기가 소실 될 수 있다.
⇒ He 초기화(He Initialization)는 이러한 치명적인 문제를 완화시키려는 목적으로 제안
He
He 초기화도 Xavier 초기화와 동일하게 이전 레이어의 노드 수에 비례하여 가중치를 초기화한다. 하지만 He 초기화는 ReLU 활성화 함수의 특성 때문에 더 큰 스케일(표준편차 좀 더 크게)을 사용한다. 이는 ReLU 활성화 함수가 음수일 때 0을 출력하므로, 더 큰 가중치로 시작하여 기울기 소실 문제를 완화하는 데 도움이 된다.
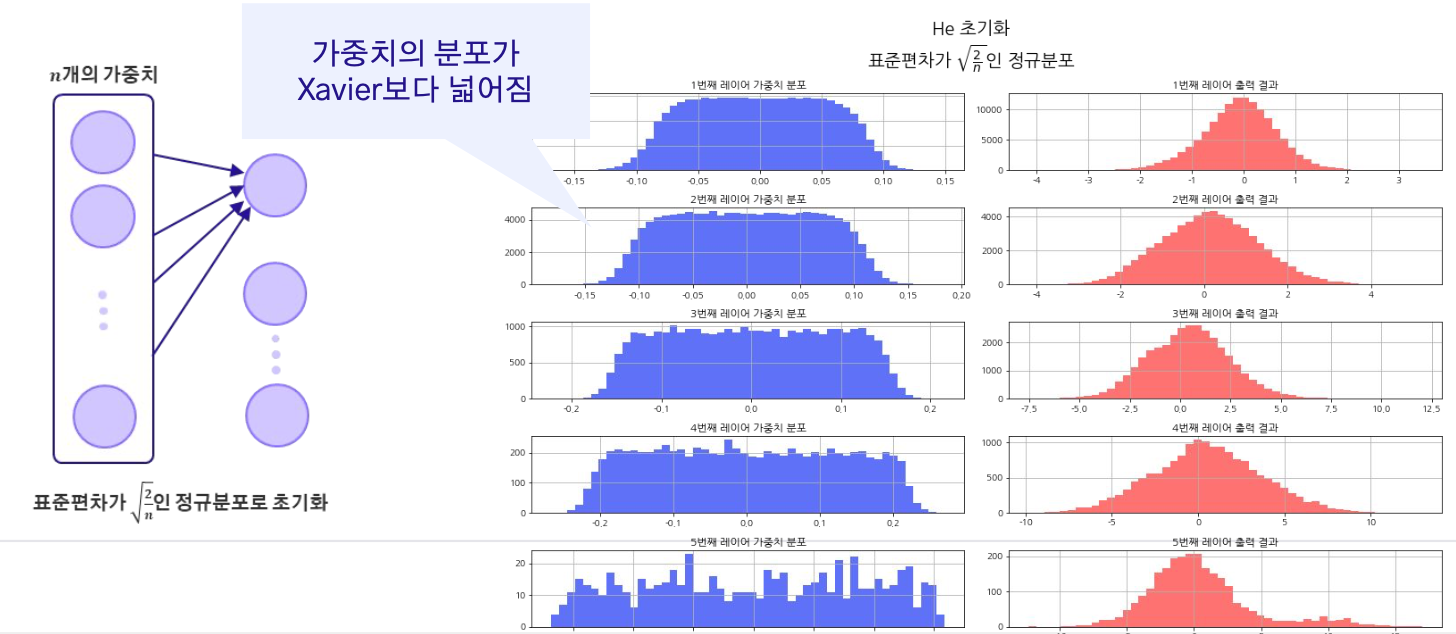
Xavier vs He
가중치 초기화를 선택할 때, 결국 어떤 활성화 함수를 선택하느냐에 달려있다.
⇒ 시그모이드와 같은 활성화 함수를 쓰게 된다면, Xavier 초기화 방법을 써보자.
⇒ ReLU와 같은 활성화 함수를 쓰게 된다면, He 초기화 방법을 써보자.
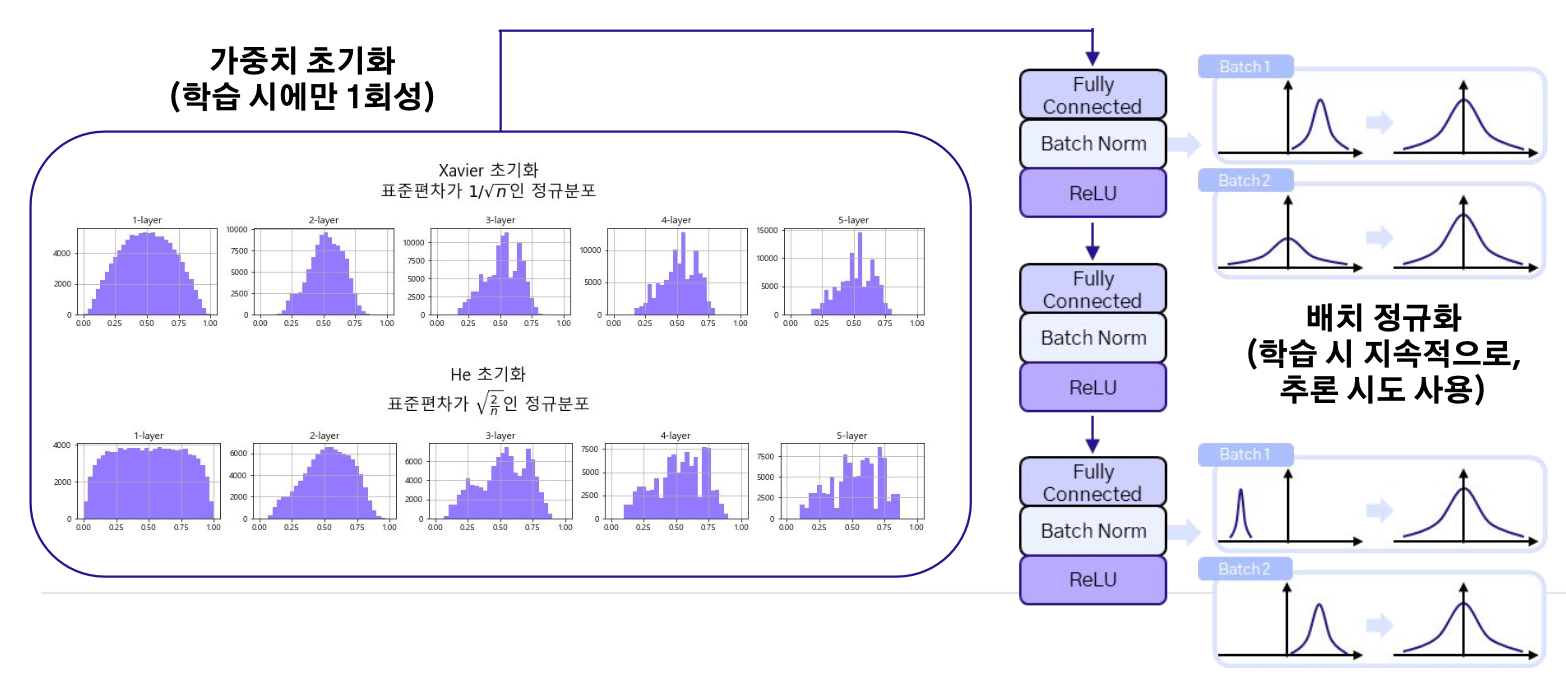
가중치 초기화 vs 배치 정규화
가중치 초기화도 데이터를 정규화하고 배치 정규화도 활성후 레이어 이후의 출력을 정규화한다는 공통점이 있다. 하지만, 두 방법은 언제 누구에게 사용되느냐에 차이점이 있다.
과적합 방지를 위한 규제화 및 학습률 조정
가중치 감쇠
큰 가중치에 대한 패널티를 부과함으로써 모델의 가중치를 작게 유지하려고 한다. 이를 통해 모델의 복잡도를 감소시켜 모델이 훈련 데이터에 과도하게 적합하는 것을 억제(훈련 데이터가 적거나, 훈련 데이터에 노이즈가 많은 경우에 유용)
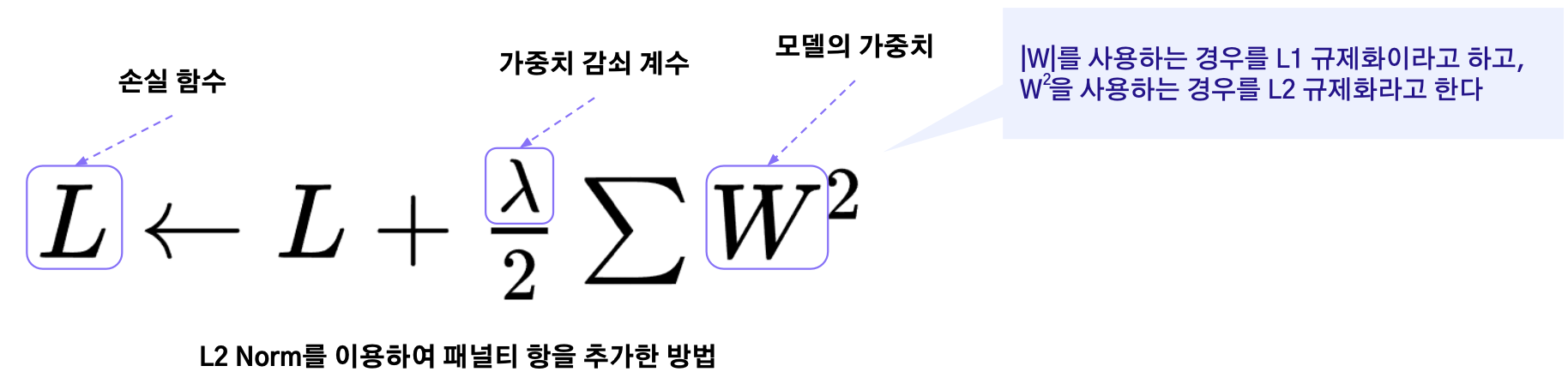
동일한 가중치 값을 갖는다면 가능하면 작은 가중치를 갖는 것이 좀 더 나은 솔루션이라는 직관
- 가중치가 크다면 상대적으로 역전파 신호가 적기 때문에 학습속도 느려짐/.
class Net:
...
def loss(self,y_pred,y_true):
"""
정답(y_true)와 예측값(y_pred)을 기반으로 손실값을 계산.
L2 정규화가 적용된 가중치 감쇠 포함.
"""
#가중치 감쇠 계산
for idx in range(1,self.hidden_layer_num+2):
W = self.params[f'W{idx}']
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W**2)
return self.last_layer.forward(y_true,y_pred) + weight_decay
> 각 레이어를 돌면서 파라미터값을 가져와서 제곱해서 더함 easyEarly stopping
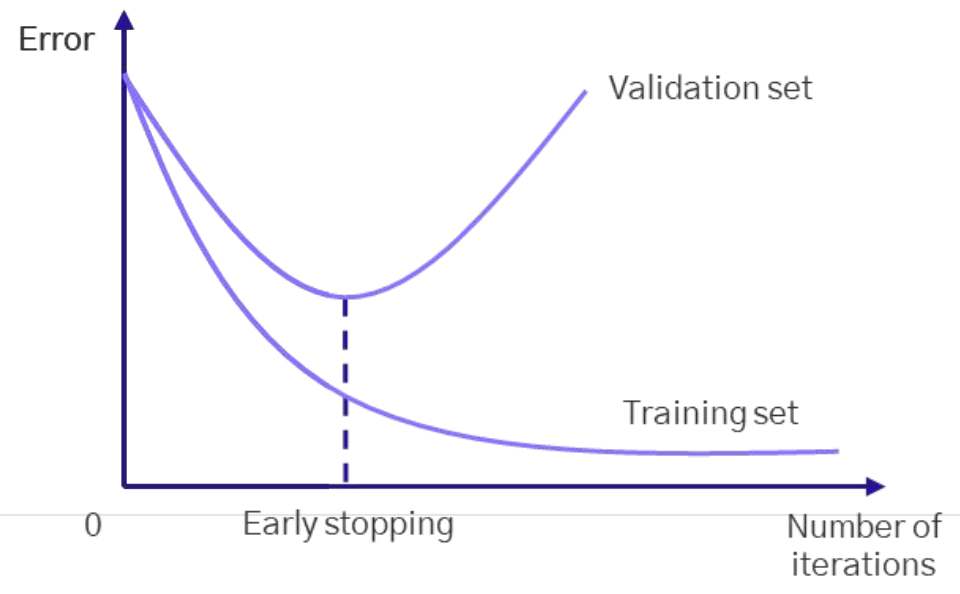
학습이 진행될수록, 모델의 학습 오차는 계속 해서 줄어들어 과적합이 되고 검증 오차는 어느 순간 증가한다. 이렇게 학습 오차는 줄어들지만 검증 오차가 줄어들지 않고 늘어나는 시점에서 학습을 중지하는 방법
Learning rate scheduler
딥러닝 훈련 과정에서 사용되는 학습률을 동적으로 조절하는 역할
- 적절한 학습률 스케줄링은 학습 속도를 빠르게함
- 로컬 미니마에서 벗어남
- 일반적으로 성능 증가하는 모델 얻도록 도움
종류
- Constant 초기에 설정한 학습률을 학습 과정 전체에 걸쳐 변경하지 않음
- Step Decay 일정한 주기(epoch 또는 iteration)마다 학습률을 일정 비율로 감소
- ex)초기 학습률을 0.1로 설정하고 50 에포크마다 학습률을 0.5배로 줄이는 경우를 고려
- Exponential Decay 학습률을 지수적으로 감소
- Cosine Annealing 코사인 함수를 따라 학습률이 감소하도록 설정
- 이는 학습률이 안정적인 감소를 보이게 하며, 일정 주기로 다시 재시작할 수 있음
- One-cycle Policy 학습률이 먼저 증가한 다음 감소하도록 설정
- 이는 빠르게 수렴하게 하고, 끝부분에서는 학습률을 감소시켜 안정적인 학습을 도움
