문제링크

첫번째 케이스

https://www.acmicpc.net/problem/2512

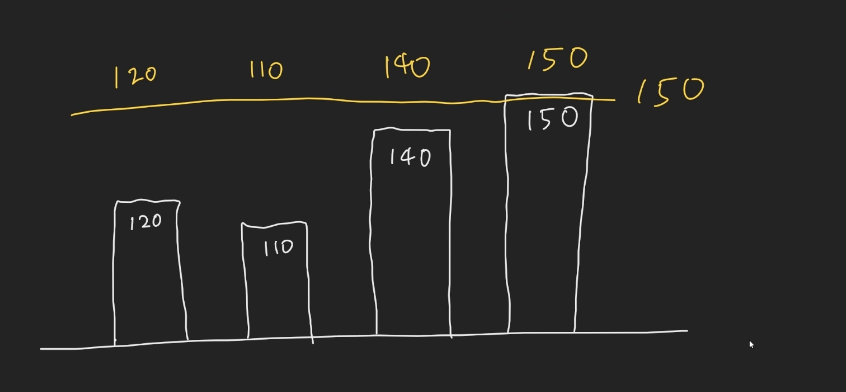
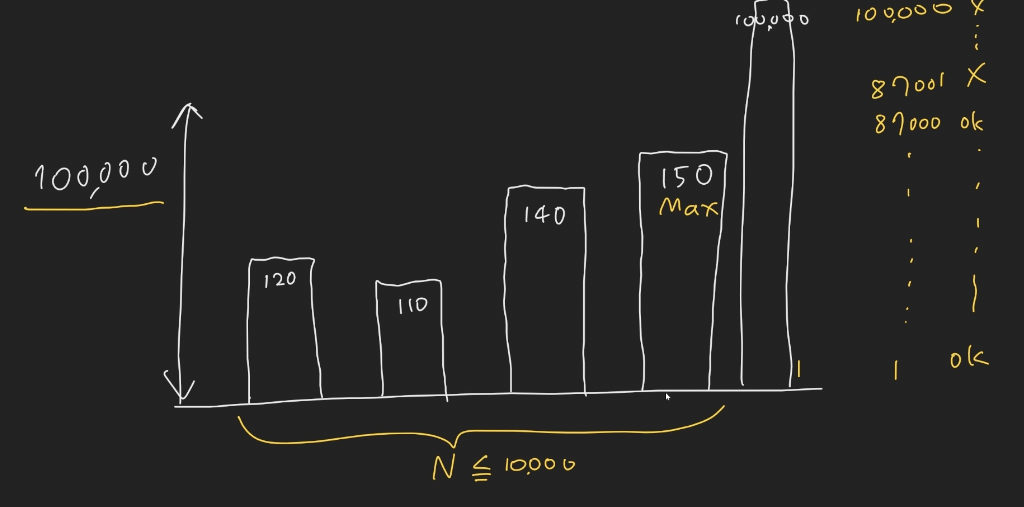
상한선을 그냥 150을 줄 경우 예산오버가 발생 예산 485보다 더 커져버림

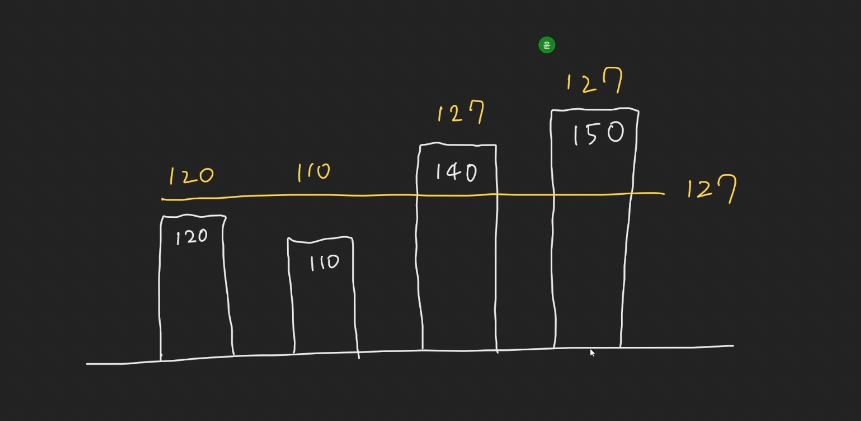
상한선을 127까지 준다면 다 더했을 때 484라서 국가 총 예산 485를 넘지 않는다. 그래서 127이 답이다.

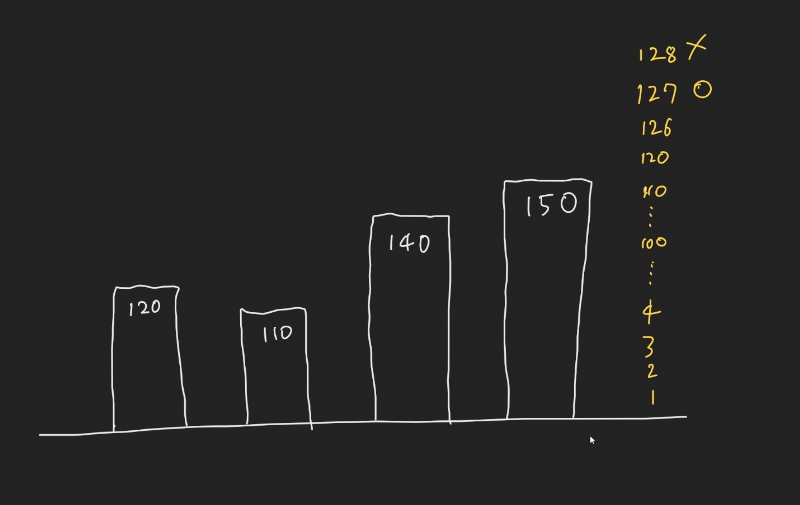
상한선을 최대한 너무 낮게나 너무 높게 줘도 다 안된다. 1부터 시작해서 128로 할 경우 안됨. 답이 127이구나 생각을 할 수 있는데 이렇게 생각하면 안됨!

입력 조건

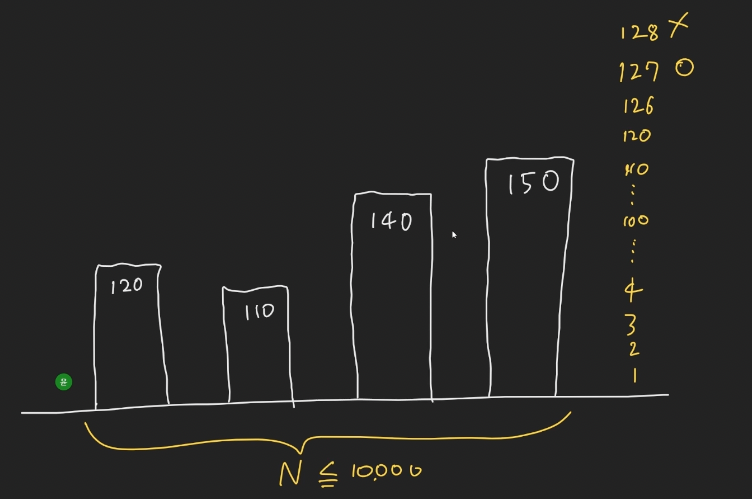
입력을 따져 보면 3 < N < 10000 이다.

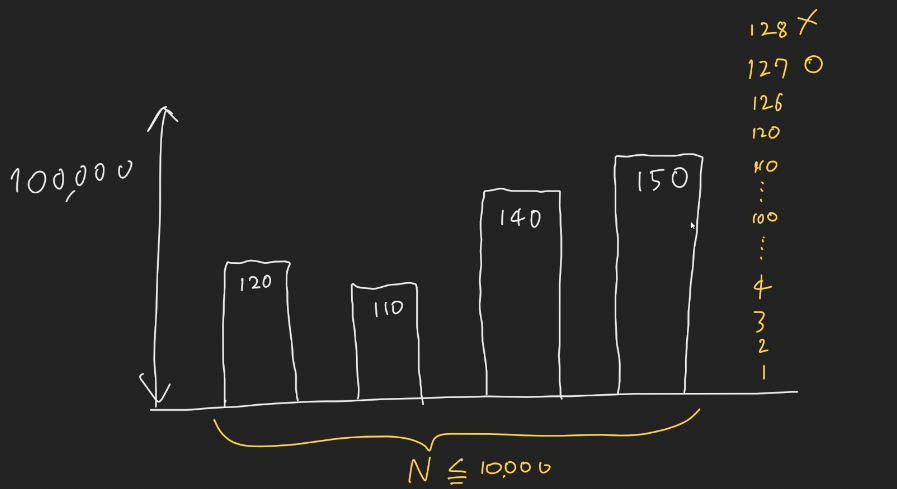
첫번째 케이스 같은 경우 127이 나왔지만 10만이하 어떤값도 나올 가능성이 있음

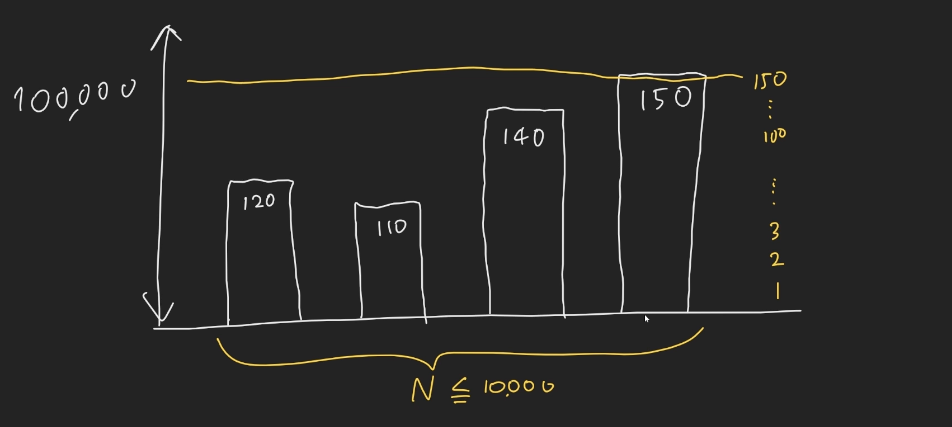
1씩 늘릴 경우 150까지 늘리면 모든 요청값을 다 만족 할 수 있다.

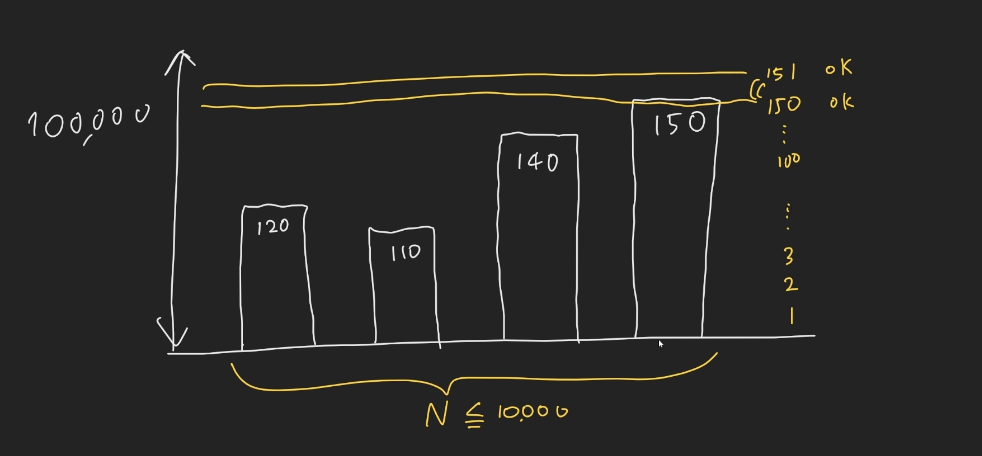
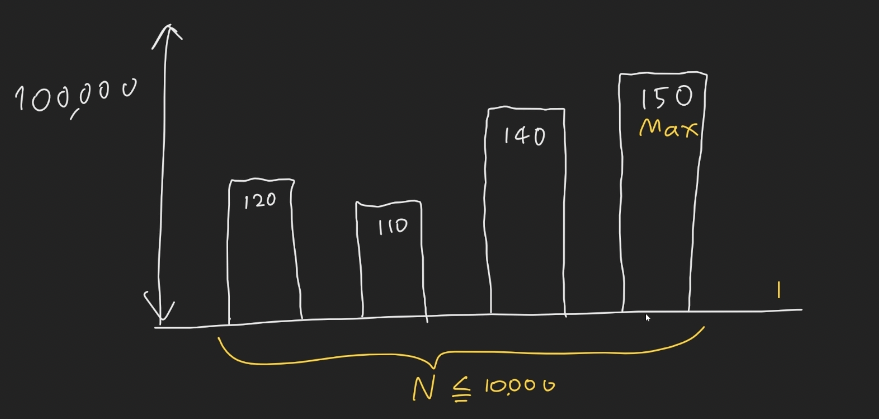
150이상도 만족 할수 있을경우 150이상도 다 ok이다. 그래서 150보다 늘리면 의미가 없는 것이다.

최적화 문제 > 결정 문제로 변경해서 이분 탐색으로 풀기

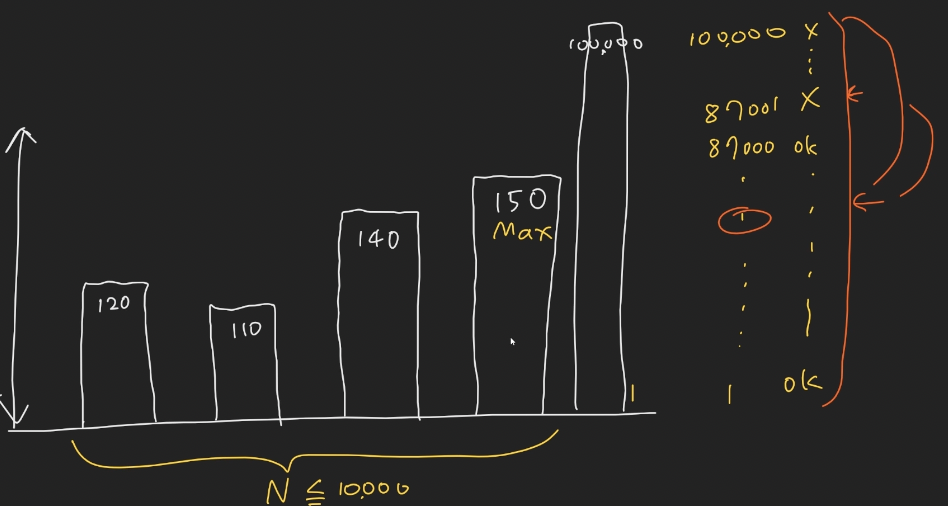
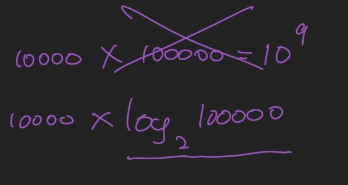
선형으로 풀면 연산이 1초에 10의 9승이므로 시간초과가 발생할 예정이고 이분으로 풀면 10000 x log2 100000이므로 괜찮을거 같음

문제풀이

중간값 출력 예제1

N = int(input())
req = list(map(int,input().split()))
M = int(input())

# lo : 작은값 hi: 높은값 mid: 중간값

lo = 0
hi = max(req)
mid = (lo + hi) // 2
answer = 0


def is_possible(mid):
    return sum(min(r, mid) for r in req) <= M


# 탐색 범위 반복
while lo <= hi:
    print(f'lo: {lo}, mid: {mid}, hi: {hi}, answer: {answer}')
    # 국가 총 예산 으로 감당이 가능 한지?
    if is_possible(mid):
        # mid 로 가능할 경우 mid 불포함
        lo = mid + 1
        answer = mid
    # 그렇지 않을 경우 상한선 을 낮은 쪽으로 탐색
    else:
        hi = mid - 1

    mid = (lo + hi) // 2
print(answer)

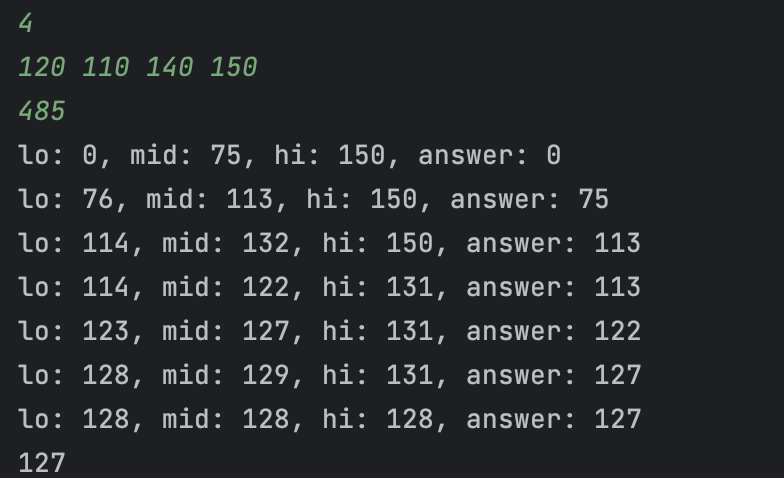
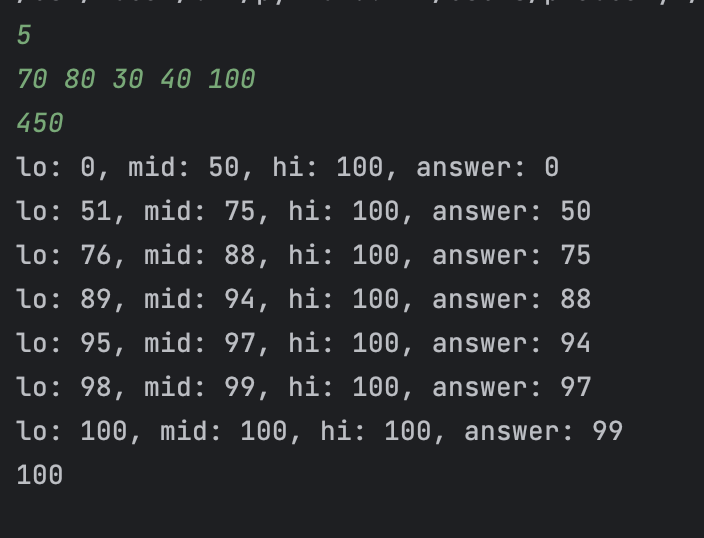
중간값 출력 예제2

전체코드

N = int(input())
req = list(map(int,input().split()))
M = int(input())

# lo : 작은값 hi: 높은값 mid: 중간값

lo = 0
hi = max(req)
mid = (lo + hi) // 2
answer = 0


def is_possible(mid):
    return sum(min(r, mid) for r in req) <= M


# 탐색 범위 반복
while lo <= hi:
    # print(f'lo: {lo}, mid: {mid}, hi: {hi}, answer: {answer}')
    # 국가 총 예산 으로 감당이 가능 한지?
    if is_possible(mid):
        # mid 로 가능할 경우 mid 불포함
        lo = mid + 1
        answer = mid
    # 그렇지 않을 경우 상한선 을 낮은 쪽으로 탐색
    else:
        hi = mid - 1

    mid = (lo + hi) // 2
print(answer)