문제링크

https://www.acmicpc.net/problem/10844

이론

f(n) : 길이가 1인 계단 총 갯수

f(n) = f(n-1) + f(n-1) ?

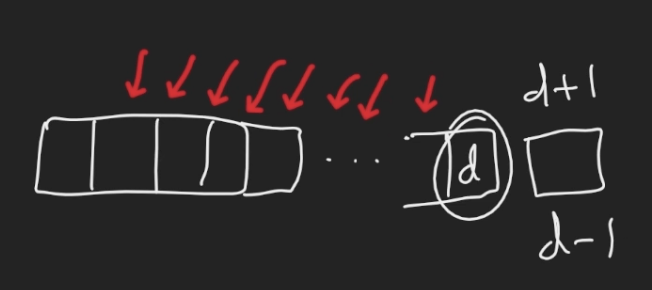
f(d, n) -> f(n + 1, d + 1)
f(d, n) -> f(n + 1, d - 1)

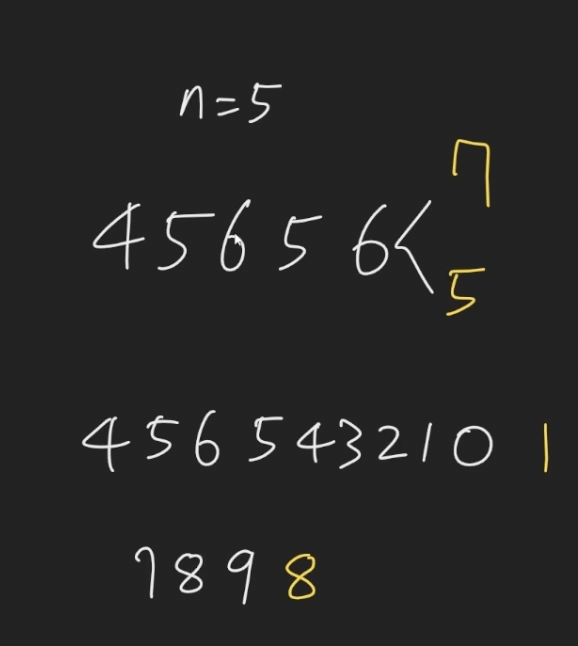
1 ~ 8 : 경우 +1 or -1

9 : -1

0 : +1

1 ~ 8 뒤는 크거나 작은 수가 들어올수 있고 9는 작은수, 0은 큰수가 들어옴

푸는 법

(f(N,0) + f(N,1) + f(N,2) + ... + f(N,9)) % MOD

f(n,d) = f(n-1, d-1) + f(n-1, d+1)

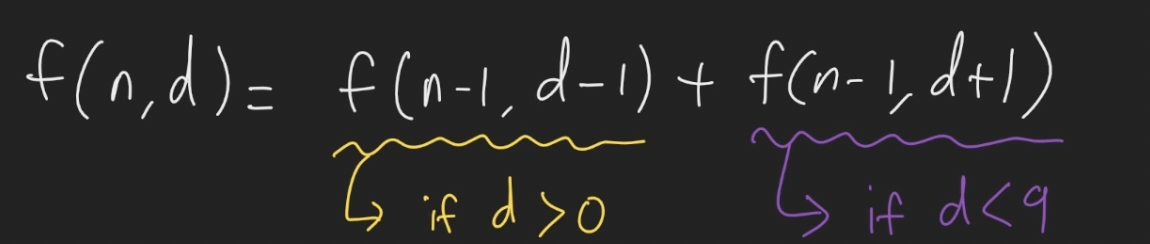
f(n-1, d-1) 는 d 가 0보다 커야하고, f(n-1, d+1)는 d가 9보다 작아야 함

전체코드

MOD = 1_000_000_000

# cache[n][d]: 길이가 n, 마지막 숫자가 계단인 개수
cache = [[0] * 10 for _ in range(101)]
for j in range(1, 10):
    cache[1][j] = 1

for i in range(2, 101):
    for j in range(10):
        if j > 0:
            cache[i][j] += cache[i-1][j-1]
            cache[i][j] %= MOD
        if j < 9:
            cache[i][j] += cache[i-1][j+1]
            cache[i][j] %= MOD

ans = 0
N = int(input())
for j in range(10):
    ans += cache[N][j]
    ans %= MOD

print(ans)