스택, 재귀 함수

함수가 호출되면 사용하는 메모리 영역

• 스택 메모리 영역

스택과 큐

• 스택
  • 데이터를 쌓아주고 젤 위에서부터 가져가는것.(후입선출)
  • 쌓인접시
• 큐
  • 들어온 순서대로 먼저 나간다(선입선출)
  • 화장실 줄

스택 메모리를 쓰는 이유는 함수가 스택이란 구조를 채택하고 있어서.

이 함수 호출 해제 순서.

void CFunc()
{

}

void BFunc()
{
	CFunc();
}

void AFunc()
{
	BFunc();
}


int main(void)
{
	AFunc();

	return 0;
}

1. main함수 호출
2. main함수에서 AFunc 호출
3. AFunc함수에서 BFunc함수 호출
4. BFunc에서 CFunc함수 호출.
5. CFunc함수 해제
6. BFunc함수 해제
7. AFunc함수 해제
8. main함수 해제.

스택 오버 플로우

• 스택 메모리는 무한하지않다.
• 유한한 스택 메모리 공간을 넘어서 쓰게되면 오류발생한다
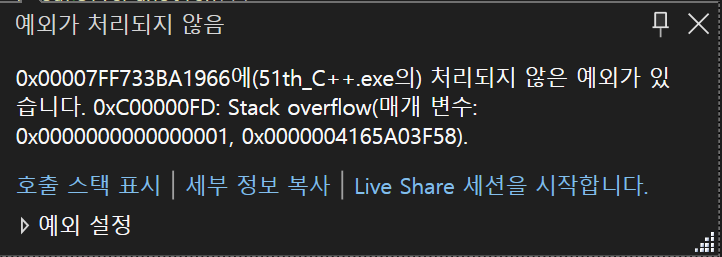
  • 스택 오버 플로우
  • 재귀 함수 종료조건이 없다면 무한 루프를 돌면서 스택 오버플로우 발생.

void RecursiveFunction()
{
	RecursiveFunction();
}

int main(void)
{
	RecursiveFunction();
    
	return 0;
}

재귀 함수

• 호출된 함수가 해당 함수(본인)을 다시 호출하는 구조
• 종료 조건이 없다면 무한 반복호출로 인한 스택 오버플로우가 발생한다.
• 간단(간결)하게 문제 해결이 가능한경우(ex 계층구조(트리) 형태 순회)

팩토리얼

• 그 수보다 작거나 같은 모든 양의 정수의 곱
  • 5! == 5 4 3 2 1;
  • 7! == 7 6 5 4 3 2 1;

for문을 이용한 팩토리얼 구현.

int Factorial(int _Num)
{
	int Result = 1;

	for (int i = 0; i < _Num; ++i)
	{
		Result *= i + 1;
	}

	return Result;
}

int main(void)
{

	int i = 0;

	i = Factorial(4);

	return 0;
}

재귀함수를 이용한 팩토리얼 구현.

int Factorial_Recusion(int _Num)
{
	// 10 ! == 10 * 9!;
	// 9 ! == 9 * 8!
	// _Num! == _Num * (_Num-1)!;

	if (1 == _Num) // 종료 조건 
	{
		return 1;
	}
	else
	{
		return _Num * Factorial_Recusion(_Num - 1);
	}
}

int main(void)
{

	int i = 0;

	i = Factorial_Recusion(4);

	return 0;
}

• 종료 조건이 없다면 무한 루프를 돌아서 스택 오버 플로우 발생하니 재귀함수는 종료조건을 무조건 써야한다.

단축키 추가

• 기본 줄 정렬
  • Ctrl 누른채로 k,f

피보나치 수열(for문)

• 전전항과 전항을 더한값이 다음 값
• 1 1 2 3 5 8 13 21 ...

int Fibonacci(int _Num)
{
	if (1 == _Num || 2 == _Num)
	{
		return 1;
	}

	// 3항 이상인 경우 처음 두항(1, 1) 부터
	// 누적해서 해당 항을 구해준다.
	int iResult = 0;

	int Prev1 = 1;
	int Prev2 = 1;

	for (int i = 0; i < _Num - 2; ++i) 
	{
		iResult = Prev1 + Prev2; 
		Prev1 = Prev2;
		Prev2 = iResult; 
	}

	return iResult;
}

int main(void)
{
	int iReturn = Fibonacci(2); //

	iReturn = Fibonacci_Recursion(10);
	iReturn = Fibonacci_Recursion(11);

}

if (1 == _Num || 2 == _Num)

• _Num값이 1이 들어온다면 뒤쪽에 2 == _Num은 연산(평가)를 안한다.

for (int i = 0; i < _Num - 2; ++i)

• 반복조건(_Num - 2)는 3항을 구한다치면 1이 들어가고 4항을 구할떄는 2가 필요하고 5항은 3

		iResult = Prev1 + Prev2
		Prev1 = Prev2;
		Prev2 = iResult;

• 저위의 2번쨰줄가 3번쨰 줄에 순서가 바뀐다면 안된다.
  • Prev2의 값이 소실 되기 떄문이다.

피보나치 수열(재귀 함수)

int Fibonacci_Recursion(int _Num)
{
	if (1 == _Num || 2 == _Num)
	{
		return 1;
	}

	return Fibonacci_Recursion(_Num - 1) + Fibonacci_Recursion(_Num - 2);
}

int main()
{
	// 피보나치 수열 구하기
	int iReturn = 0;

	iReturn = Fibonacci_Recursion(10);
	iReturn = Fibonacci_Recursion(11);

	iReturn = Fibonacci_Recursion(48);


	return 0;
}

if (1 == _Num || 2 == _Num)
{
	return 1;
}

• 종료 조건
  • 1과 2과 들어오면 1을 반환해서 종료한다.

재귀 함수의 장단점

• 장점
  1. 코드가 간결해진다.
  2. 코드의 직관성이 더 높다.
• 단점
  1. 느리다.(매우중요)

재귀함수가 느린이유.

• 피보나치 수열을 재귀로 구현할 경우, 높은 항을 구할려면 엄청난 함수 호출 횟수가 발생한다.
• 피보나치 48을 구하고 싶다면 계산이 엄청 오래 걸린다.
  • 최초 48항을 구하기 위해서 최소 계산당 2번의 게산을 해야한다 그게 돌아오고 계속 쌓이면 크다.
  • 피보나치가 아래 값을 구하려 내려갈수록 2^지수 만큼의 연산을 해야한다.
    • 48을 구할려면 2^48 + 2^48 + ... 2^2 + 2^1 함수호출해야한다.

재귀함수 큰수를 호출하면 스택 오버 플로우가 발생하지않는 이유?

• 48을 호출한다해도 호출스택의 깊이는 48층이기 떄문이다.
• 이 과정에서 발생한 함수 호출 횟수는 수천억에서 조단위까지 가능하고 한번에 발생하는 층의 깊이는 48층이기 때문이다.

강의 코드

#include <iostream>

void RecursiveFunction()
{
	RecursiveFunction();
}

// 팩토리얼
int Factorial(int _Num)
{
	int Result = 1;

	for (int i = 0; i < _Num; ++i)
	{
		Result *= i + 1;
	}

	return Result;
}

int Factorial_Recusion(int _Num)
{
	if (1 == _Num)	
		return 1;	
	else	
		return _Num * Factorial_Recusion(_Num - 1);	
}


// 피보나치 수열
int Fibonacci(int _Num)
{
	if (1 == _Num || 2 == _Num)
	{
		return 1;
	}	
    
	int iResult = 0;
	int Prev1 = 1;
	int Prev2 = 1;

	for (int i = 0; i < _Num - 2; ++i)
	{
		iResult = Prev1 + Prev2;

		Prev1 = Prev2;
		Prev2 = iResult;
	}

	return iResult;
}

// 피보나치 수열(재귀)
int Fibonacci_Recursion(int _Num)
{
	if (1 == _Num || 2 == _Num)
	{
		return 1;
	}

	return Fibonacci_Recursion(_Num - 1) + Fibonacci_Recursion(_Num - 2);
}


int main()
{
	//RecursiveFunction();
	int i = 0;
	
	i = Factorial(10);
	i = Factorial_Recusion(10);

	if (i == 10)	
		i = 10;
	

	// 피보나치 수열 구하기
	int iReturn = 0;
	
	iReturn = Fibonacci(3);
	iReturn = Fibonacci(4);
	iReturn = Fibonacci(2000);
	
	iReturn = Fibonacci_Recursion(10);
	iReturn = Fibonacci_Recursion(11);

	iReturn = Fibonacci_Recursion(48);

	return 0;
}

1차 23.12.05
2차 23.12.06
3차 23.12.07
4차 23.12.11
5차 23.12.17
6차 23.12.24
7차 24.01.01
8차 24.01.22