[Python] 멀쩡한 사각형

문제

문제 링크

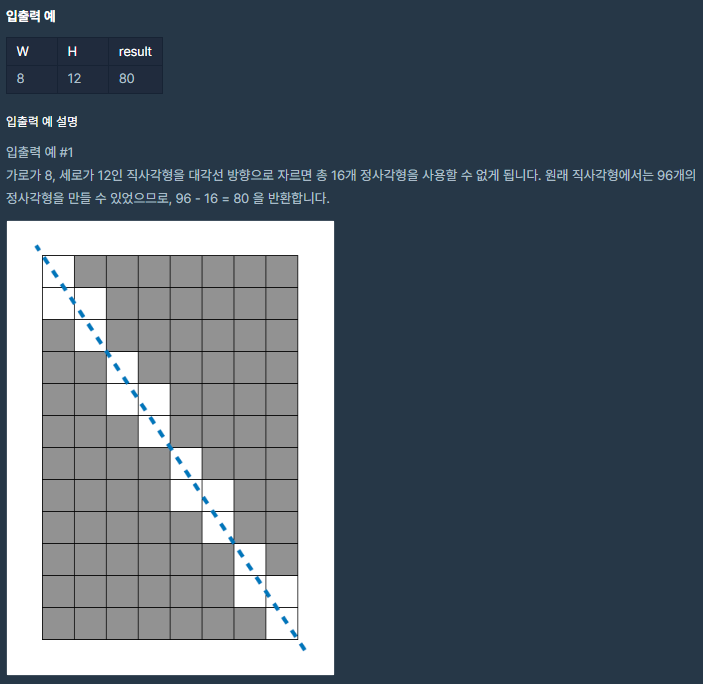
풀이

---

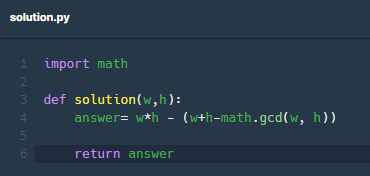
어렵고 어떤 구조는 찾았지만 해결 방법이 아닌 것 같아.. 결국 다른 사람의 코드를 보고 풀었다.
처음 접근했던 구조는

• n*n 의 경우 -n을 빼는 것
• n*(n+1) 의 경우 -2n을 빼는 것
• n*(n+2) 의 경우 -2n+1을 빼는 것
• n*(n+3) 의 경우 -2n을 빼는 것
• n*(n+4) 의 경우 -3n을 빼는 것
• n*(n+5) 의 경우 -3n+1을 빼는 것
• n*(n+6) 의 경우 -3n을 빼는 것
• n*(n+7) 의 경우 -4n을 빼는 것
• n*(n+8) 의 경우 -4n+1을 빼는 것
• n*(n+9) 의 경우 -4n을 빼는 것
  ...
  처럼 계산되는 것이다. 하지만 답에 접근하고 있지 않는다는 생각이 들었다.

---

다른 사람의 풀이를 참고하여 풀었을 때
동일하게 반복되는 패턴을 찾아야 한다!
좌표로 반복되는 좌표는 [0, 0] 제외하고,
[2, 3], [4, 6], [6, 9], [8, 12] 으로
x 좌표는 2씩 증가하고, y좌표는 3씩 증가한다.
반복되는 좌표 모양에서 직선이 지나가 제외되는 사각형의 수는 4개이다.
주어진 값 8과 12가 4와 무슨 관련이 있는지 생각해보면
바로 최대공약수인 것이다. 이때, 최대공약수가 1인 경우와 1이 아닌 경우를 나누어 생각해야한다!

---

최대공약수가 1인 경우

• w=2, h=3일 때, 4개의 사각형을 제외한다.
  w+h - 1 = 2+3-1 =4

---

최대 공약수가 1이 아닌 경우

• w=6, h=12일 때, 12개의 사각형을 제외한다.
  [0, 0] 제외하고
  [1, 2],[2, 4], [3, 6], [4, 8], [5, 10], [6, 12]이 반복되어
  x는 1씩 증가, y는 2씩 증가한다.
  반복되는 좌표 모양에서 직선이 지나가 제외되는 사각형의 수는 2개이다.
  6과 12의 최대 공약수는 6이다.
  최대 공약수는 반복되는 패턴이 일어나는 횟수로
  w+h-최대공약수(gcd)로 6+12-6 = 12가 나온다

---

그리하여 전체 사각형의 개수에서 제외되는 사각형을 빼는 것으로 반복되는 공식은
(전체 사각형 개수) - (제외되는 사각형)
(w*h) - (w+h-gcd)가 된다.

출처

결과

해석 및 기억할 부분

Git

• math 라이브러리를 사용하여 최대 공약수를 구하는 함수 gcd()를 사용할 수 있음