인덱스란
인덱스는 데이터베이스에서 검색 속도를 향상시켜준다. key, value 형태로 정렬되어 책의 목차처럼 빠르게 어떤 정보에 접근할 수 있도록 도와준다.
정렬되어 있기 때문에 데이터를 찾을 때 테이블 전체를 풀 스캔 할 필요 없이 정렬된 인덱스에서 원하는 데이터를 찾을 수 있다. 또 특정 범위, 최대, 최소 값을 찾는데도 유리하다.
그렇다면 테이블의 모든 컬럼에 인덱스를 지정하면 될텐데, 실제로 그렇게 데이터베이스를 디자인 하지 않는다.
인덱스의 장단점
왜냐하면 인덱스 자체를 저장할 추가 공간이 필요하기 때문이다. 인덱스는 데이터베이스 내 로그에 저장되는데, 인덱스가 많으면 많을수록 해당 테이블의 용량이 커지게 된다.
또 인덱스 자체가 정렬되어 있기 때문에 데이터를 추가, 삭제하는데에 있어서 관리 리소스가 들어간다.
심지어 인덱스를 잘못 사용하게 되면 검색 성능이 안좋아지는 경우가 있다. 이런 경우 쿼리의 실행 계획을 잘 확인해서 인덱스를 잘 타고 데이터를 찾도록 해줘야 한다.
즉 인덱스를 생성할 컬럼에 대한 전략이 꼭 필요하다. 인덱스는 인덱스가 필요할 만큼의 규모가 있는 테이블에 생성해야 한다.
또 추가, 삭제에 있어서 인덱스를 다시 재정렬해야 하는 경우가 있으므로 추가, 삭제가 빈번하지 않는 테이블이어야 한다.
또 데이터의 중복도가 높으면 검색하는 것보다 테이블 전부를 가져오는 편이 효율적이므로 데이터의 중복도가 낮은 테이블에 인덱스를 설정하는 것이 맞다.
인덱스의 자료구조
이러한 인덱스는 몇 가지 자료구조를 통해 만들어진다. 그 중 가장 대표적인 3가지인 해시 테이블, B-Tree, B+Tree에 대해 알아보자.
해시 테이블
해시 테이블은 key, value 형태로 데이터를 저장한다. key를 통해 값에 바로 접근하므로 검색 시 O(1)의 복잡도로 빠르게 데이터를 찾을 수 있다.
하지만 key의 등호 연산에만 유리하고 쿼리에서 자주 사용되는 부등호 연산에는 불리하다.
B-Tree
B-Tree에 대해 알아보기 전에 왜 데이터베이스에서 일반적인 Tree가 아닌 B-Tree를 사용하는지에 대해 알아보자.
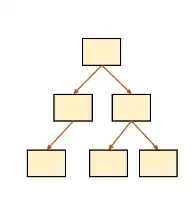
일반적으로 트리는 이렇게 생겼다. 인덱스는 정렬이 되어 있기 때문에 분할정복 방식으로 평균 O(logN)의 시간 복잡도로 트리 내에서 데이터를 찾을 수 있다.
하지만 어떤 데이터가 추가되고 삭제 될지 모른다. 산전수전을 다 겪은 테이블은 이런 형태가 될 수도 있다.
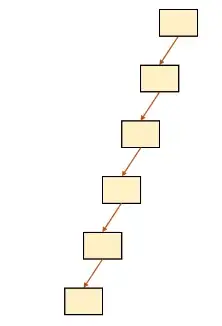
이렇게 한 쪽으로 편향된 트리는 검색을 위해 모든 노드를 순회 해야하므로검색 성능이 O(N)까지 떨어질 수 밖에 없다.
그래서 데이터베이스에서는 B Tree를 사용한다. B는 Balanced의 약자로 언제나 같은 높이의 트리를 유지하기 때문에 검색 성능을 유지 시킬 수 있다.
B-Tree는 아래와 같이 생겼다.
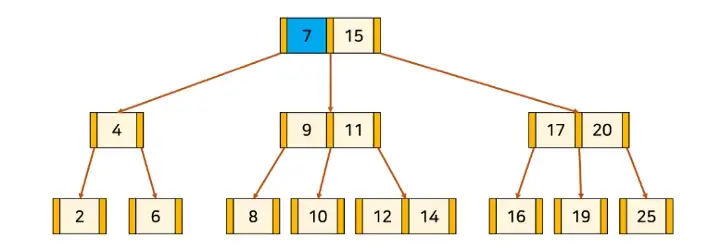
값을 찾기 위해서 일반적인 트리처럼 좌, 우측만을 사용하지 않고 노드에 저장된 값 사이의 포인터를 통해 탐색한다.
위 그래프에서 14라는 값을 찾는다고 하면, 14는 7,15 사이에 있으므로 가운데 연결된 (9, 11) 노드로 내려가고 14는 11보다 크므로 11의 오른쪽 노드로 내려가서 14라는 값에 도달하게 된다.
실제로는 한 노드에 많은 값들이 정렬된 상태로 존재한다.
노드가 추가 되거나 삭제 될 때는 한 노드에 얼마나 많은 값들이 존재할 수 있는지 체크를 하고 값을 맨 아래 리프노드의 적절한 위치에 넣은 후 제 자리를 찾아가게 된다.
예를 들면 13이라는 값이 추가 되면 최초에는 (12,14) 노드 사이에 들어간다. 하지만 한 노드에 2개 값만 존재할 수 있으므로(위 트리의 경우에만) 13이 한 단계 한 단계 레벨을 올리며 자기 자신의 자리를 찾아가게 된다.
이 과정을 페이징이라고 한다.
B+Tree
B-Tree는 데이터의 검색에는 유리하다. 하지만 모든 데이터를 풀 스캔하려면 모든 트리를 전부 방문해야 한다.
이러한 단점을 개선한 것이 B+Tree이다.
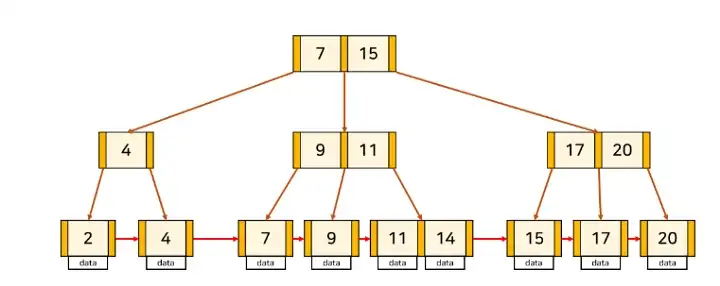
B+Tree는 리프 노드에만 데이터를 저장하고 모든 리프노드를 Linke List를 통해 연결한다.
이렇게 하면 리프노드를 제외한 루트, 브랜치 노드에는 데이터를 저장하지 않기 때문에 메모리가 남고 그 남는 메모리를 중간 브랜치 노드에 키 값을 저장하는데 사용할 수 있다.
즉 트리의 높이가 낮아지므로 검색 속도가 빨라진다.
또 테이블 풀스캔을 하는 경우에도 리프 노드에 어차피 모든 데이터가 있고 모두 Linked List로 연결되어 있으므로 풀 스캔시에도 B-Tree 보다 유리하다.범위 스캔을 하는 경우에도 LinkedList를 통해 효울적인 순차 검색을 할 수 있다.
하지만 B+Tree는 모든 데이터가 리프노드에 있기 때문에 값을 찾기 위해서 어떻게든 리프노드에 도달해야만 하고 브랜치 노드에서 키를 올바르게 찾아가기 위해 중복된 키가 존재할 수도 있다.
