문제
👀 문제 사이트 : https://www.acmicpc.net/problem/2042
풀이
난이도 : Gold I
이 문제는 숫자들이 나열되어 있을 때 중간에 값을 바꾸거나 지정된 구간의 합을 구하는 문제이다.
그냥 배열에 값을 저장하고 구간합을 계속 구하는 방식을 사용하면 시간초과가 난다.
수의 개수는 n은 1,000,000 이하이고, 구간의 합을 구하는 수 K는 10,000이하이므로 곱해서 비교만 해봐도 1000억번 정도가 되고 시간복잡도는 O(NK) 이기 때문이다.
여기서 해결방법으로 Segment Tree 를 사용하였는데, 그 이유는 Segment tree의 장점을 사용할 수 있는 것들이 모두 이 문제에 포함되어 있기 때문이다.
👀 Segment Tree
Segment Tree란 주어진 array에서 다양한 range query들을 update와 함께 지원하는 자료구조이다.
이 Segement Tree를 이용하면 구간 합을 구하거나 값을 바꾸는데 O(log n) 안에 완료할 수 있다.
✔ build
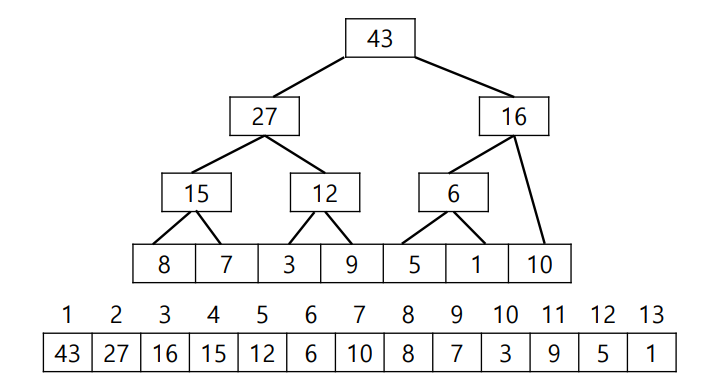
- 각 구간의 합들을 array로 표시하며, left child는 2n, right child는 2n+1 위치에 작성하여 tree array를 구성한다.
✔ update
- 만약 7을 6으로 변경한다고 하면, tree에서 parent에 해당하는 node들만 값을 따라서 변경해주면 되기 때문에
O(log(n)) 시간 안에 완료된다.
✔ rangesum
- 만약 인덱스가 2~5 구간 안에 있는 값들을 모두 더하는 연산을 진행한다면 7, 12(3+9), 5를 선택하면 되고,
인덱스가 4~7 구간 안에 있는 값들이라면 9, 16((5+1)+10) 을 선택하여 더해주면 된다.
(인덱스 1~7까지 [8,7,3,9,5,1,10] 이라고 가정)
- 따라서 양 끝에 관련된 인덱스만 주의하면서 탐색을 진행하다가 범위 안에 포함되는 값들은 바로 선택하여 구할 수 있기 때문에 rangesum 연산 또한 O(log(n)) 안에 완료할 수 있다.
✔ 주의할 점
- python3로 제출하면 시간초과가 나오므로 pypy3로 제출해야한다.
코드
n, m, k = map(int, input().split())
tree = [0] * (10*n)
numbers = []
for _ in range(n):
numbers.append(int(input()))
def segment_tree_build(node, start, end):
if start == end:
tree[node] = numbers[start-1]
else:
mid = (start + end) // 2
segment_tree_build(2*node, start, mid)
segment_tree_build(2*node+1, mid+1, end)
tree[node] = tree[2*node] + tree[2*node+1]
def segment_tree_rangesum(node, start, end, left, right):
if start > right or end < left:
return 0
if start >= left and end <= right:
return tree[node]
mid = (start + end) // 2
p1 = segment_tree_rangesum(2*node, start, mid, left, right)
p2 = segment_tree_rangesum(2*node+1, mid+1, end, left, right)
return p1 + p2
def segment_tree_update(node, start, end, idx, val):
if start == end:
numbers[idx-1] = val
tree[node] = val
else:
mid = (start + end) // 2
if start <= idx and idx <= mid:
segment_tree_update(2*node, start, mid, idx, val)
else:
segment_tree_update(2*node+1, mid+1, end, idx, val)
tree[node] = tree[2*node] + tree[2*node+1]
segment_tree_build(1, 1, n)
results = []
for _ in range(m+k):
a, b, c = map(int, input().split())
if a == 1:
segment_tree_update(1, 1, n, b, c)
elif a == 2:
results.append(segment_tree_rangesum(1, 1, n, b, c))
for result in results:
print(result)