문제를 읽고 바로 생각한것은
시작지점에서 BFS 알고리즘을 사용해서 k번 안에 탈출 지점에 도달할 수 있는 모든 경우의 수를 확인한다.
입니다.
#include <string>
#include <vector>
#include <iostream>
#include <queue>
using namespace std;
int map[55][55];
int dix[4] = { 1,0,0,-1 };
int diy[4] = { 0,-1,1,0 };
char route[4] = { 'd','l','r','u' };
string solution(int n, int m, int x, int y, int r, int c, int k) {
queue<pair<int, int>> cur;
queue<pair<string, int>> result;
cur.push({ x,y });
result.push({ "",0 });
while (cur.size() > 0) {
int xx = cur.front().first;
int yy = cur.front().second;
cur.pop();
string str = result.front().first;
int cnt = result.front().second;
result.pop();
if (cnt == k && xx == r && yy == c) {
return str;
}
else if (cnt < k) {
for (int i = 0; i < 4; i++) {
int dx = xx + dix[i];
int dy = yy + diy[i];
if (dx >= 1 && dx <= n && dy >= 1 && dy <= m) {
cur.push({ dx,dy });
result.push({ str + route[i],cnt + 1 });
}
}
}
}
return "impossible";
}
-
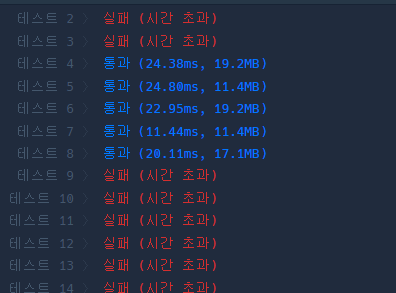
시간 초과 발생
k의수가 <2500 으로 시간초과가 발생하는 듯합니다!
다른 방법을 생각한것은 탈출한 경로를 문자열로 나타내었을때에, 문자열이 사전 순으로 가장 빠른 경로로 탈출해야하기때문에 l,r,u,d를 사전 순으로 정리하자면 d,l,r,u 가 되고 즉, 이 말은
탈출지점이 시작지점보다 밑이라면 d로 먼저 위치를 맞춰주고 좌우를 진행합니다, 위라면 위로가는 것이아닌 좌우부터 이동을 해주어서 맞춰주고 상하를 맞춥니다. 이는 사전순으로 리턴할 것 이기때문에 가능합니다.
또한가지 문제에서 주어진 예시처럼 시작지점과 탈출점의 거리는 3이고 k는 5이기때문에
도달할 수 있는 것입니다(다시 돌아갔다가 원위치를 하면된다) 하지만 k가 4라면 도달하지 못할 것입니다. 이를 이용해서 예외처리를 해줍니다.
- 하지만 이 방법을 작성하는 중에 너무 많은 예외사항이 었었습니다
왼쪽으로 쭉 가서 다시 돌아온다, 하지만 왼쪽에 벽이있는경우,
아래로 쭉 내려가서 다시 돌아온다, 하지만 아래에 벽이있는경우, 처럼 예외 사항이 너무 많았습니다.
- 결국 시간초과를 해결하지 못하고 해답을 보았다.
해답은 DFS를 사용하는 방법과 그리디 방법이있었다.
신기한것은 DFS로 해결하는 풀이는 방법은 내가작성한 BFS방법과 유사했지만 걸리는 시간을 훤씬더 효율적이였다. 이유를 찾아보니 DFS의 백트래킹 성질때문에 시간을 줄이기가 가능했다고 한다.
아직 BFS와 DFS가 어떤 문제에 효율적인지에대해서 잘 알지 못하는 것 같아서 공부하고 넘어간다.
밑에 내용은 공부하면서 도움이 될것같은 문장을 가져왔다.
DFS와 BFS 문제에 적용하는 팁
- 그래프의 모든 정점을 방문하는 것이 주요한 문제
단순히 모든 정점을 방문하는 것이 중요한 문제의 경우 DFS, BFS 두 가지 방법 중 어느 것을 사용하셔도 상관없습니다.
둘 중 편한 것을 사용하시면 됩니다.
경로의 특징을 저장해둬야 하는 문제- 예를 들면 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용합니다. (BFS는 경로의 특징을 가지지 못합니다)
- 최단거리 구해야 하는 문제
미로 찾기 등 최단거리를 구해야 할 경우, BFS가 유리합니다.
왜냐하면 깊이 우선 탐색으로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만,
너비 우선 탐색으로 현재 노드에서 가까운 곳부터 찾기 때문에경로를 탐색 시 먼저 찾아지는 해답이 곧 최단거리기 때문입니다.- 검색 대상 그래프가 정말 크다면 DFS를 고려
- 검색대상의 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS
출처
-DFS 를 적용시킨 코드는
#include <string>
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
using namespace std;
int map[55][55];
int dix[4] = { 1,0,0,-1 };
int diy[4] = { 0,-1,1,0 };
char route[4] = { 'd','l','r','u' };
bool findAnswer;
string result;
string answer;
void DFS(int cnt, int x, int y, int n, int m, int r, int c, int k) {
if (findAnswer == true) { //답을 찾은경우
return;
}
if (abs(x - r) + abs(y - c) > k - cnt) { //결과가 나올 수 없는 경우
return;
}
if (x == r && y == c && cnt == k) { //답을 찾은 경우
findAnswer = true;
answer = result;
return;
}
for (int i = 0; i < 4; i++) {
int dx = x + dix[i];
int dy = y + diy[i];
if (dx >= 1 && dx <= n && dy >= 1 && dy <= m) {
result += route[i];
DFS(cnt + 1, dx, dy, n, m, r, c, k);
result.pop_back();
}
}
}
string solution(int n, int m, int x, int y, int r, int c, int k) {
int distance = abs(x - r) + abs(y - c);
if (k < distance || (k - distance) % 2 == 1) {
return "impossible";
}
DFS(0, x, y, n, m, r, c, k);
return answer;
}내가 찾고자하는 도착 지점이 아니거나, 현재 위치에서 도착지점까지 도달할 수 없다면 백트래킹으로 돌려주면서 답을 찾는다.
- 그리디 방법
#include <string>
#include <vector>
using namespace std;
int distance(int x, int y, int r, int c){
return abs(x-r)+abs(y-c);
}
string solution(int n, int m, int y, int x, int c, int r, int k) {
string answer = "";
while(k > 0){
--k;
if(y < n && distance(x,y+1,r,c) <= k) {answer += "d"; y+=1;}
else if(x > 1 && distance(x-1,y,r,c) <= k) {answer += "l"; x-=1;}
else if(x < m && distance(x+1,y,r,c) <= k) {answer += "r"; x+=1;}
else if(y > 1 && distance(x,y-1,r,c) <= k) {answer += "u"; y-=1;}
else if(k == 0) return "impossible";
}
return answer;
}그리디는 참 간단했다 우선순위가 d -> l -> r -> u 순서이기때문에 각각의 방향을 갈 수 있는지 체크해줌과 동시에 이동했을때에 도착지점으로 갈 수 있는지를 확인하고 이동하는 것이였다.
많은 문제를 풀어보고 경험도 많이 했다고 생각했는데 아직 부족한 점이 더 많은 것 같다.
문제를 보고 무작정 해결하려고 들지 말고, 어떤 알고리즘을 적용시켜야하는지 어떻게 하면 효율적인지를 생각하는 습관을 기르자!!

