프로그래머스 43165 타겟 넘버 - Lv2

문제 링크

https://school.programmers.co.kr/learn/courses/30/lessons/43165

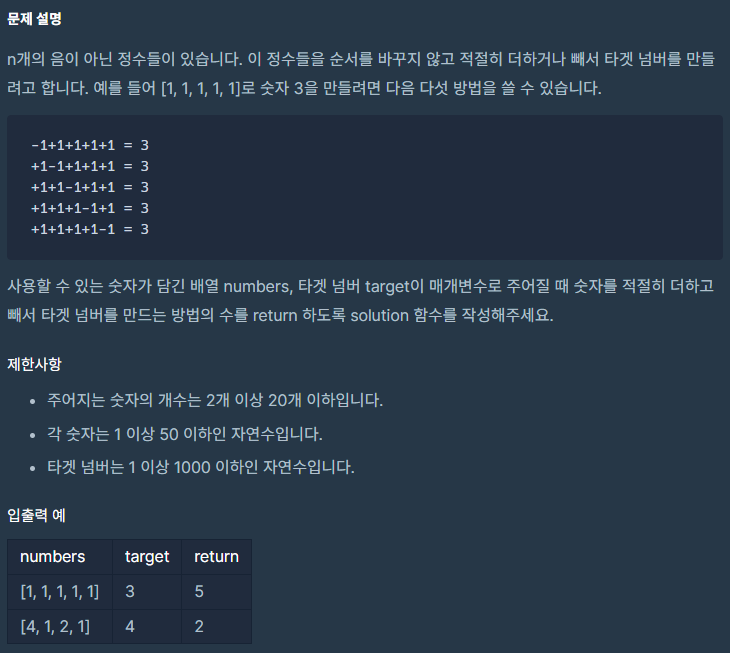
문제 설명

문제 분석

• 그래프 탐색의 필요성

  • 먼저, 주어진 자연수들로 만들 수 있는 수식들은 + 를 - 로 바꿔주면 서로를 오갈 수 있음(1)
  • 또한, 우리가 알고 싶어하는 '타겟 넘버를 만드는 방법의 수'가 곧 수식의 수이므로,
    우리는 모든 수식을 탐색하면서 이 수식이 타겟 넘버를 만드는지 확인해야 함(2)
  • (1) -> 그래프로 표현하기 편함
    (2) -> 그래프 탐색으로 풀기 편함

• 중간에 탈출하는 조건의 필요성

  • 예로 numbers = [4, 3, 2, 1], target = 4 를 생각해볼 때, 나올 수 있는 모든 수식의 갯수는
    2 ** 4 이므로 16개가 존재함. 여기서 모든 자연수가 더해진 수식 '+ 4 + 3 + 2 + 1'을 출발점으로
    하고, 왼쪽부터 각 자연수들 앞에 있는 +를 -로 바꿔주면서 탐색을 한다고 가정할 때, 몇 가지 수식은 탐색의 필요성이 없는 경우가 존재함.

  • 예 : + 4 - 3 - 2 □ 1 의 경우 뒤에 있는 1 앞에 +가 오든 -가 오든 상관없이 target 값이 못 됨
    => 아 어느 방향으로 탐색하다가 target 값보다 작아지면 탐색을 종료해야 하는구나!

  • 또한, 주어진 숫자가 20개가 될 수 있기 때문에 수식을 vertex로 잡는다고 할 때, vertex 100만 개짜리 그래프에서 탐색을 해야 하므로 중간에 탈출하는 조건은 필수적인듯

• 결국 어떻게 풀거냐?

  • (1) 수식을 그래프 형식으로 표현해서 탐색을 한다 (BFS든 뭐든)
    • (1-1) 근데 수식 100만 개는 좀 심하니까 숫자로 그래프를 만들고 거기서 bt을 하는 게 좋지 않을까?
  • (2) 탐색을 하다가 target 값보다 작아지면 탈출을 한다

• Pseudo Code

def bt(x):
    if x.sum < target: return (2)
    if x.sum == target: answer += 1

    new_x <- new x
    bt(new_x)

st <- 모든 자연수를 더한 수식
bt(st)
print(answer)

코드

class bt:
    def __init__(self, numbers, target):
        self.answer = 0
        self.numbers = numbers
        self.target = target
    
    def run(self):
        total_sum = sum(self.numbers)    
        if total_sum < self.target:
            return 0
        
        self.numbers.sort()
        self.visited = [0] * len(self.numbers)
        
        self.bt_(total_sum)
        return self.answer
    
    def bt_(self, s, v = 0):
        if s < self.target:
            return
        if s == self.target:
            self.answer += 1
            return
        
        for i in range(v, len(self.numbers)):
            if self.visited[i] == 0:
                self.visited[i] = 1
                self.bt_(s - self.numbers[i] * 2, i)
                self.visited[i] = 0

def solution(numbers, target):
    back_tracking = bt(numbers, target)
    answer = back_tracking.run()
    return answer