백준 트리의 순회(2263) - 골드 Ⅰ

문제 링크

https://www.acmicpc.net/problem/2263

문제 요약

1부터 n까지 번호가 중복 없이 매겨진 노드로 이진 트리가 있다고 하자. 이 이진 트리의 중위 순회와 후위 순회가 주어졌을 때 전위 순회를 구하시오.

• 예시
  

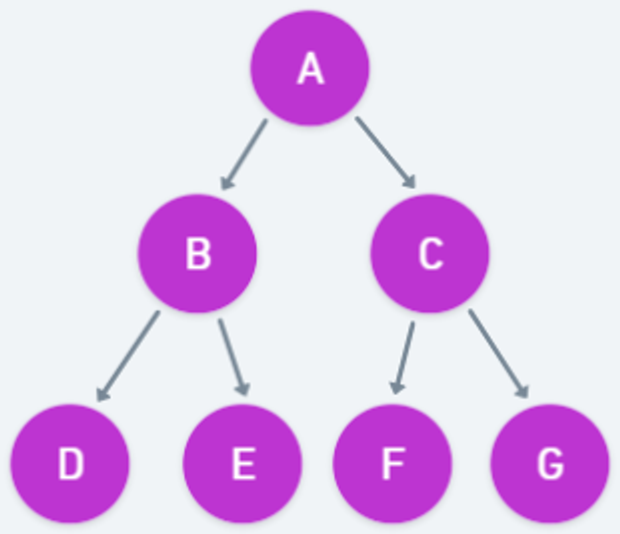
  • 이진 트리 예시. 이건 문제에서 알려주지 않음

  • 입력
    D B E A F C G
    D E B F G C A

  • 정답
    A B D E C F G

  • 실제 주어지는 이진 트리는 완전 이진 트리가 아닐 수 있음!

입출력

• 입력
  첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.
• 출력
  첫째 줄에 프리오더를 출력한다.

문제 분석

• 트리 순회의 특징을 이용하는 문제이므로 딱히 어떤 유형의 문제라고 하기가 어려운 거 같음. 굳이 분류하면 분할정복법?
• 트리 순회의 특징을 생각했을 때, 중위 순회는 무조건 가운데에 최상위 루트 노드를 두고 왼쪽과 오른쪽에 하위 트리가 존재하며, 후위 순회는 무조건 마지막에 최상위 루트 노드가 존재한다.
• 또한 후위 순회에서는 중위 순회에서 나오는 왼쪽과 오른쪽 하위 트리들이 (내부 순서는 좀 다르지만) 차례로 나온 다음에 최상위 루트 노드가 나온다.
• 그리고 이런 성질은 하위 트리에서도 똑같이 성립한다.
  예시
  D B E A F C G (중위)
  D E B F G C A (후위)
  D B E (중위, 좌측 하위 트리)
  D E B (후위, 좌측 하위 트리)
  

풀이 전략

1. 루트 노드를 찾고 결과에 추가한다. 그리고 그 왼쪽 하위 트리와 오른쪽 하위 트리를 찾는다.
   1. 어떻게 이걸 함?
      1. 후위 순회 결과에서 맨 마지막에 있는 노드를 찾는다. 이게 루트 노드다.
      2. 찾은 루트 노드를 중위 순회 결과에서 찾는다.
      3. 중위 순회 결과에서 루트 노드 왼쪽이 왼쪽 하위 트리이고 오른쪽이 오른쪽 하위 트리이다.
2. 1을 재귀적으로 반복한다.

의사 코드

bt <- 주어진 이진 트리, binary tree
answer = "" # 반환할 답 

def pre_order(bt):
		global answer
		
		if bt is empty or not exist: return		

		# 1. 루트 노드를 찾고 결과에 추가한다
		# 후위 순회 결과에서 맨 마지막에 있는 노드를 찾는다. 이게 루트 노드다.
		root = post-order(bt)[-1]
		answer += f" {root}" # 결과에 추가
		
		# 1. 그리고 그 왼쪽 하위 트리와 오른쪽 하위 트리를 찾는다.
		# 찾은 루트 노드를 중위 순회 결과에서 찾는다.
		idx = in-order(bt).index(root)
		# 중위 순회 결과에서 루트 노드 왼쪽이 왼쪽 하위 트리이고 
		# 오른쪽이 오른쪽 하위 트리이다.

		# 2. 재귀적으로 반복한다.
		pre_order(bt[:idx])
		pre_order(bt[idx+1 :])

print(answer)

몇 가지 잔기술

• in-order 탐색 결과에서 root 노드의 위치를 매번 찾지 말고 따로 저장하면 좋다

in_order_loc = [0 for _ in range(len(in_order) + 1)]
for i, node in enumerate(in_order): in_order_loc[node] = i

• bt 자체를 인자로 쓰면 메모리 사용량이 늘어나기 때문에 bt의 시작점과 끝나는 점의 위치 정보를 전달하는 게 좋다.

  def pre_order(in_st, in_end, post_st, post_end):
  		...

  • in_order

    0 → in_st			3 → idx			6 → in_end - 1
    D	B	E	A	F	C	G
    0		2		4		6
    in_st		idx - 1		idx + 1		in_end - 1

  • post_order

    0 → post_st						6 → post_end - 1
    D	E	B	F	G	C	A
    0		2	3		5
    post_st		post_st + 2	+1		post_end - 2

코드

1. 기본 세팅

import sys
limit_number = 10 ** 9
sys.setrecursionlimit(limit_number)

1. 입력 받기

N = int(input())
in_order = tuple(map(int, sys.stdin.readline().rstrip().split()))
post_order = tuple(map(int, sys.stdin.readline().rstrip().split()))

in_order_loc = [0 for _ in range(len(in_order) + 1)]
for i, node in enumerate(in_order): in_order_loc[node] = i

1. pre_order 함수 정의 및 실행

answer = "" # 반환할 답 

def pre_order(in_st, in_end, post_st, post_end):
        global answer, N, in_order, post_order

        if (in_st >= in_end) or (post_st >= post_end):
            return
        
        # 1. 루트 노드를 찾고 결과에 추가한다
        # 후위 순회 결과에서 맨 마지막에 있는 노드를 찾는다. 이게 루트 노드다.
        root = post_order[post_end - 1]
        answer += f" {root}" # 결과에 추가

        # 1. 그리고 그 왼쪽 하위 트리와 오른쪽 하위 트리를 찾는다.
        # 찾은 루트 노드를 중위 순회 결과에서 찾는다.
        idx = in_order_loc[root] 
        left_count = idx - in_st # 왼쪽 하위 트리의 갯수

        # 중위 순회 결과에서 루트 노드 왼쪽이 왼쪽 하위 트리이고 
        # 오른쪽이 오른쪽 하위 트리이다.

        # 2. 재귀적으로 반복한다.
        pre_order(in_st, idx, post_st, post_st + left_count)
        pre_order(idx + 1, in_end, post_st + left_count, post_end - 1)

pre_order(0, len(in_order), 0, len(post_order))
print(answer[1:])