대학 과제 - 단편(Radix 정렬)

문제

입출력 예시

문제 분석

데이터(문자열)의 성질 : 앞의 Radix가 절대적으로 중요하다

• 문자열을 사전식으로 정렬할 때, 아주 중요한 점은 앞에 있는 Radix가 뒤에 있는 Radix보다 절대적으로 중요하다는 점
• 예를 들어, 'azzzzz' 와 'baaaa'를 정렬한다고 하면 뒤에 있는 z나 a와 관계 없이 맨 앞에 있는 a와 b의 비교로 둘의 순서가 결정됨
• 이런 성질을 이용해서 Bucket 정렬을 변형해서 응용할 수 있겠다는 생각을 할 수 있음
• 예를 들어 아래의 표 첫번째 열이 데이터로 주어졌다고 하자. 만약 우리가 k=2, 즉 첫번째, 두번째, 세번째로 작은 데이터를 찾는다고 하면, 맨 앞이 a인 데이터가 5개이기 때문에 우리가 찾는 데이터는 반드시 맨 앞이 a여야 함
  
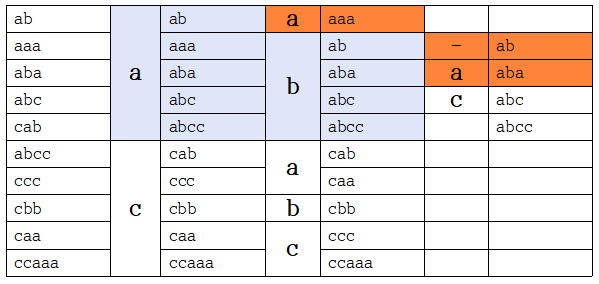
• 따라서 맨 앞이 a인 데이터들만 다시 Bucket 정렬을 실시. 이런 과정을 계속 반복하다보면 우리가 원하는 데이터를 찾을 수 있음
• 이 방법의 장점은 아래와 같음
  1. 각 데이터의 모든 값을 이용하지 않아도 된다.
  2. 모든 데이터를 비교하지 않아도 된다.

생각해볼 점 : Complexity

• 다만, 위의 방법은 한 가지 문제가 있는데, Bucket 정렬을 계속 실시하는 과정에서 점점 더 Case들이 많아진다는 점
• 위의 표에서는 a, b, c만을 사용해서 경우의 수가 많지 않지만, 실제로는 한 번 bucket 정렬을 실시할 때마다 경우의 수가 27배(알파벳 26개 + 공백 1개)로 늘어남
• 따라서 generic 정렬을 구현할 때처럼 critical size 미만으로는 다른 정렬 알고리즘을 사용하는 것이 좋을 수도 있음
• 다만, 이번 문제의 경우는 데이터 갯수가 100개 밖에 되지 않고, 찾아야 하는 데이터의 갯수도 3개 밖에 되지 않아, 위의 방식으로 충분히 답을 찾아낼 수 있음

의사코드

Bucket Sort:
	Input D : Data, id : index of instance in D
	Input T_0 : A set of target ranks
	
	I <- a set of index id. {0, 1, 2, 3 ...}
	p <- 0

	SI = [[0, 1, 2, 3, ...]]
	T = [None for t in T_0]
	
	while :
		B = [[], ...]

		for I in SI:
			newB <- [[], [], ...]

			for i = 0 to len(I) do:
				key = D[i]
				newB[key[p]].append(key)
			
			for i = 0 to len(newB) do:
				if len(newB[i]) > 0 : B.append(newB[i])

		I <- []
		tot <- 0

		for i = 0 to len(B) do:
			tot += len(B[i])

			for j = 0 to len(T) do:
				if T[j] is finded: continue
				if tot == T_0[j] and len(B[i]) == 1:
					T[j] <- B[i][0]
			
			if every t in T is finded:
				return {t}			
			
			maxT <- maximum of unfinded target ranks
			minT <- minimum of unfinded target ranks	
			
			if tot > maxT:
				while tot > minT:
					I = [B[i]] + I
					tot -= len(B[i])
					i -= 1
				break
		
		T_0 = [ t - tot for t in T_0]
		p += 1

코드

import sys

k = int(sys.stdin.readline())
D = []


while True:
  inp = sys.stdin.readline()
  if len(inp) == 0: break
  else: D.append(inp)


def bucket_finding(k):
  global D

  T_0 = [k-1, k, k+1]
  T_0_ = [k-1, k, k+1]

  SI = [range(len(D))]
  p = 0
  T = [None for t in T_0]
  minT = k-1
  maxT = k+1

  while p < 101:
    B = []

    for I in SI:
      newB = [ [] for _ in range(27) ]

      for i in I:
        key = D[i]

        if p >= len(key):
          newB[0].append(i)
        else:
          newB[ord(key[p]) - ord('a') + 1].append(i)
      
      for b in newB:
        if len(b) > 0 : B.append(b)


    SI = []
    tot = 0

    for i in range(len(B)):
      tot += len(B[i])

      check = True
      for j in range(len(T)):
        if not T[j] is None: continue
        else:  
          if tot == T_0[j] and len(B[i]) == 1:
            T[j] = B[i][0]

          else: check = False
      
      if check:
        return [ t+1 for t in T]
      
      T_None = [T_0[j] for j in range(len(T)) if T[j] is None]
      if len(T_None) >0 :
        minT = min(T_None)
        maxT = max(T_None)

      if tot > maxT:
        while tot >= minT:
          SI = [B[i]] + SI
          tot -= len(B[i])

          if i == 0: break
          else: i -= 1
        break
    
    
    T_0 = [ t - tot for t in T_0]
    p += 1

bucket_finding(k)