ArrayList의 내부 구조와 작동 방식에 대해서 설명해주세요.
ArrayList
ArrayList는 자바에서 제공하는 가변 크기의 배열로, 자바 컬렉션 프레임워크의 일부이다. 내부적으로는 배열을 사용해서 데이터를 저장하며, 그 크기는 동적으로 변경될 수 있다.
작동 방식
-
초기화: ArrayList가 생성될 때, 기본적으로 10개의 원소를 저장할 수 있는 배열이 생성된다. 이 크기는 개발자가 원하는대로 지정할 수 있다.
-
원소 추가: ArrayList에 원소를 추가하면, 원소는 배열의 끝에 추가된다. 만약 배열이 이미 꽉 차있으면, ArrayList는 새로운 배열을 생성하고 기존의 원소들을 새 배열로 복사합니다. 이 새 배열의 크기는 기존의 배열 크기의 1.5배로 설정된다.
-
원소 제거: ArrayList에서 특정 원소를 제거하면, 제거된 원소 뒤의 모든 원소들이 앞으로 한 칸씩 이동합니다. 이로 인해 배열의 연속성이 유지된다.
-
원소 검색: ArrayList에서 특정 원소를 찾으려면, 인덱스를 통해 직접 접근할 수 있습니다. 이는 ArrayList가 배열을 기반으로 하기 때문에 가능한 기능하다.
LinkedList
LinkedList는 자바의 컬렉션 프레임워크 중 하나로, 이중 연결 리스트를 기반으로 한다. 이중 연결 리스트는 각각의 노드가 이전 노드와 다음 노드에 대한 참조를 가지고 있다는 특성이 있다.
작동 방식
-
초기화: LinkedList는 생성될 때 비어있는 상태로 시작한다. 즉, 처음에는 아무런 노드도 포함하지 않는다.
-
원소 추가: LinkedList에 원소를 추가하면, 새로운 노드가 생성되고 이전 노드와 다음 노드에 대한 참조가 설정된다. 리스트의 처음이나 끝, 또는 특정 위치에 원소를 추가할 수 있다.
-
원소 제거: LinkedList에서 원소를 제거하면, 해당 노드의 이전 노드와 다음 노드가 서로 연결된다. 그리고 제거된 노드는 가비지 컬렉션에 의해 메모리에서 제거된다.
-
원소 검색: LinkedList에서 원소를 찾으려면, 처음 노드부터 시작해서 찾고자 하는 원소를 찾을 때까지 노드를 하나씩 방문한다. 이런 특성 때문에 원소 검색은 LinkedList에서 상대적으로 느린 작업이 될 수 있다.
ArrayList와 LinkedList의 성능 차이는 무엇인가요? ArrayList와 LinkedList 중 어느 것을 사용하는 것이 더 좋을까요?
ArrayList vs LinkedList
ArrayList와 LinkedList는 모두 리스트 형태의 자료구조이지만, 내부 구조와 작동 방식의 차이로 인한 성능 차이가 있다.
-
인덱스 접근: ArrayList는 인덱스를 이용한 데이터 접근이 빠른 편이다. 왜냐하면 내부적으로 배열을 사용하기 때문에 인덱스를 통해 바로 데이터를 참조할 수 있기 때문이다. LinkedList는 데이터 접근 시 첫번째 노드부터 순차적으로 접근해야하기 때문에 인덱스 접근이 느리다.
-
데이터 추가/삭제: ArrayList는 데이터 추가/삭제 시 배열의 크기를 변경해야 하고, 이를 위해 배열 복사가 이뤄지기 때문에 속도가 느린 편이다. 반면에 LinkedList는 노드의 연결만 변경하면 되기 때문에 데이터 추가/삭제가 빠른 편이다. 따라서 데이터 개수가 많지 않고 인덱스를 통한 접근이 빈번하다면 ArrayList를 사용하는 것이 좋고, 데이터의 추가/삭제가 빈번하고 데이터 접근은 순차적이고 빈번하지 않으면 LinkedList를 사용하는 것이 좋다.
리스트의 특정 위치에 데이터를 삽입하거나 삭제할 때 ArrayList와 LinkedList는 어떤 차이가 있나요? 성능 차이는 어떻게 될까요?
ArrayList는 내부적으로 배열을 사용하기 때문에, 특정 위치에 데이터를 삽입하거나 제거할 때 해당 이후의 모든 요소들을 앞뒤로 이동시켜야 한다.
반면 LinkedList는 각 요소가 이전 요소와 다음 요소의 참조를 갖는 노드 형태로 구성되어 있다. 따라서 특정 위치의 데이터를 삽업/삭제 시킬때는 해당 노드의 참조만 변경하면 된다. 이는 상대적으로 빠르게 처리할 수 있다.
그러나 LinkedList에서 특정 위치를 찾기 위해 처음부터 순차적으로 탐색해야 하므로, 중간에 데이터를 삽입하거나 삭제하는 경우 탐색 시간이 추가로 필요하다.
결국, 특정 위치에 대한 데이터 삽입/삭제는 ArrayList와 LinkedList 모두 최악의 경우 시간 복잡도 O(n)이 될 수 있다. 이는 리스트 크기에 비례하여 시간이 걸린다는 것을 의미한다.
public class Main {
public static void main(String args[]) {
List<String> arrayList = new ArrayList<>();
List<String> linkedList = new LinkedList<>();
for (int i = 0; i < 10000; i++) {
arrayList.add("item" + i);
linkedList.add("item" + i);
}
long startTime = System.nanoTime();
arrayList.remove(5000);
long endTime = System.nanoTime();
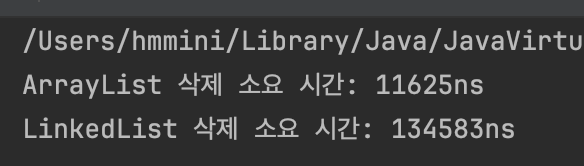
System.out.println("ArrayList 삭제 소요 시간: " + (endTime - startTime) + "ns");
startTime = System.nanoTime();
linkedList.remove(5000);
endTime = System.nanoTime();
System.out.println("LinkedList 삭제 소요 시간: " + (endTime - startTime) + "ns");
}
}
public class Main2 {
public static void main(String args[]) {
List<String> arrayList = new ArrayList<>();
List<String> linkedList = new LinkedList<>();
long startTime = System.nanoTime();
for(int i=0; i < 10000; i++) {
arrayList.add(0, "item" + i);
}
long endTime = System.nanoTime();
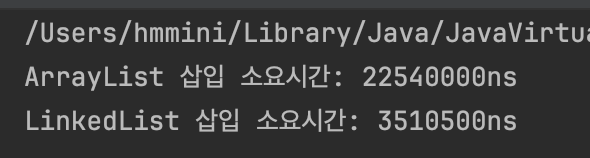
System.out.println("ArrayList 삽입 소요시간: " + (endTime - startTime) + "ns");
startTime = System.nanoTime();
for(int i=0; i < 10000; i++) {
linkedList.add(0, "item" + i);
}
endTime = System.nanoTime();
System.out.println("LinkedList 삽입 소요시간: " + (endTime - startTime) + "ns");
}
}
자료구조: 시간 복잡도와 트리 기반 자료구조
삽입 혹은 삭제할 때의 시간 복잡도의 최악 경우 O(n)이라고 했는데, 이를 해결하기 위해 다른 자료구조를 사용할 수는 없을까요?
삽입이나 삭제 작업에서 시간 복잡도가 O(n)이라는 것은 원소의 개수에 따라 성능이 선형적으로 저하될 수 있다는 것을 의미한다. 이런 문제를 해결하기 위해 사용할 수 있는 다른 자료구조는 트리 기반의 자료구조가 있다.
예를 들어, 이진 탐색 트리(Binary Search Tree, BST)는 트리의 균형을 유지하는 경우, 삽입이나 삭제 작업의 시간 복잡도를 O(log n)으로 줄일 수 있다. 여기서 log n은 이진 로그를 의미하는데, 이는 원소의 개수가 두 배로 늘어나도 작업 시간이 한 단계만 증가한다는 것을 의미한다. 하지만, 이진 탐색 트리도 삽입이나 삭제 작업에 따라 트리의 균형이 깨질 수 있고, 이런 경우에는 최악의 경우 시간 복잡도가 O(n)이 될 수 있다. 이를 해결하기 위해 AVL 트리나 레드-블랙 트리 같은 균형 이진 트리를 사용하면 된다. 이런 균형 이진 트리는 삽입이나 삭제가 일어날 때마다 자동으로 트리의 균형을 유지하기 때문에, 모든 작업의 시간 복잡도를 O(log n)으로 유지할 수 있다.
그러므로, 삽입이나 삭제 작업이 빈번하고 그에 따른 성능 저하를 최소화하고 싶다면, 균형 이진 트리 같은 자료구조를 고려해 보는 것이 좋다. 하지만 이런 자료구조는 구현이 복잡하고, 메모리 사용량이 많을 수 있으므로, 사용 사례에 따라 적절한 선택을 해야 한다.
이진 탐색 트리와 균형 이진 트리: 구현 복잡성과 메모리 사용량
이진 탐색 트리와 균형 이진 트리의 구현 복잡성과 메모리 사용량을 어떻게 평가하고 선택해야 할까요?
이진 탐색 트리(Binary Search Tree, BST)와 균형 이진 트리(AVL 트리나 레드-블랙 트리 등) 모두 트리 구조를 갖는 자료구조이지만, 그 구현 복잡성과 메모리 사용량은 다르다.
-
구현 복잡성: BST는 기본적인 트리 구조로, 구현이 비교적 간단하다. 반면에 균형 이진 트리는 삽입이나 삭제가 일어날 때마다 트리의 균형을 유지하는 로직이 추가로 필요하다. 이로 인해 구현이 복잡하고, 디버깅이 어려울 수 있다.
-
메모리 사용량: BST와 균형 이진 트리 모두 각 노드가 데이터와 왼쪽/오른쪽 자식 노드에 대한 참조를 저장해야 해서 비슷한 메모리를 사용한다. 하지만 균형 이진 트리는 추가적으로 각 노드의 높이나 색상 등의 정보를 저장해야 하므로 약간 더 많은 메모리를 사용할 수 있다.
이진 탐색 트리(Binary Search Tree, BST)
public class Node {
int key;
Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}public class BinaryTree {
private Node root;
public Node getRoot() {
return root;
}
void insert(int key) {
root = insertRec(root, key);
}
Node insertRec(Node root, int key) {
if (root == null) {
root = new Node(key);
return root;
}
if (key < root.key) {
root.left = insertRec(root.left, key);
}
else if (key > root.key) {
root.right = insertRec(root.right, key);
}
return root;
}
void delete(int key) {
root = deleteRec(root, key);
}
Node deleteRec(Node root, int key) {
if (root == null) {
return root;
}
if (key < root.key) {
root.left = deleteRec(root.left, key);
} else if (key > root.key) {
root.right = deleteRec(root.right, key);
} else {
if (root.left == null) {
return root.right;
} else if (root.right == null) {
return root.left;
}
root.key = minValue(root.right);
root.right = deleteRec(root.right, root.key);
}
return root;
}
int minValue(Node root) {
int minValue = root.key;
while (root.left != null) {
minValue = root.left.key;
root = root.left;
}
return minValue;
}
void insertAt(Node root, int key, int position) {
if (root == null) {
return;
}
if (position == 0) {
Node newNode = new Node(key);
newNode.left = root.left;
root.left = newNode;
} else if (position == 1) {
Node newNode = new Node(key);
newNode.right = root.right;
root.right = newNode;
}
insertAt(root.left, key, position - 1);
insertAt(root.right, key, position - 1);
}
}public class Main {
public static void main(String args[]) {
BinaryTree tree = new BinaryTree();
long startTime = System.nanoTime();
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
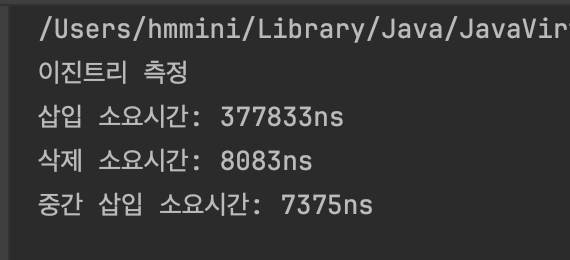
System.out.println("이진트리 측정");
long endTime = System.nanoTime();
System.out.println("삽입 소요시간: " + (endTime - startTime) + "ns");
startTime = System.nanoTime();
tree.delete(20);
endTime = System.nanoTime();
System.out.println("삭제 소요시간: " + (endTime - startTime) + "ns");
startTime = System.nanoTime();
tree.insertAt(tree.getRoot(), 20, 1);
endTime = System.nanoTime();
System.out.println("중간 삽입 소요시간: " + (endTime - startTime) + "ns");
}
}
균형 이진 트리(AVL 트리나 레드-블랙 트리 등)
public class Node {
int key, height;
Node left, right;
Node(int d) {
key = d;
height = 1;
}
}public class AVLTree {
private Node root;
int height(Node N) {
if (N == null) {
return 0;
}
return N.height;
}
Node rightRotate(Node y) {
Node x = y.left;
Node T2 = x.right;
x.right = y;
y.left = T2;
y.height = Math.max(height(y.left), height(y.right)) + 1;
x.height = Math.max(height(x.left), height(x.right)) + 1;
return x;
}
Node leftRotate(Node x) {
Node y = x.right;
Node T2 = y.left;
y.left = x;
x.right = T2;
x.height = Math.max(height(x.left), height(x.right)) + 1;
y.height = Math.max(height(y.left), height(y.right)) + 1;
return y;
}
}
