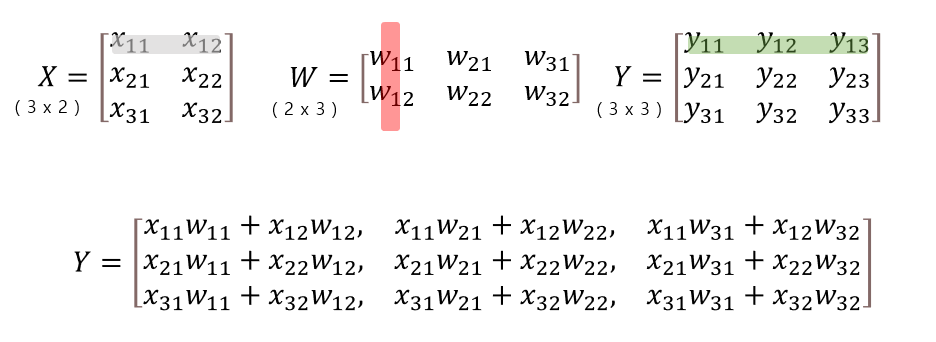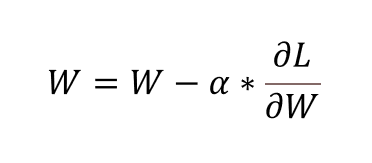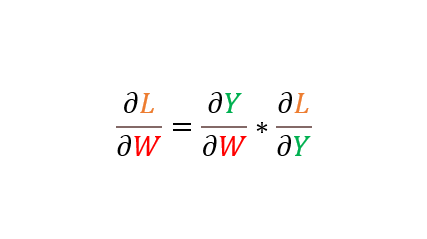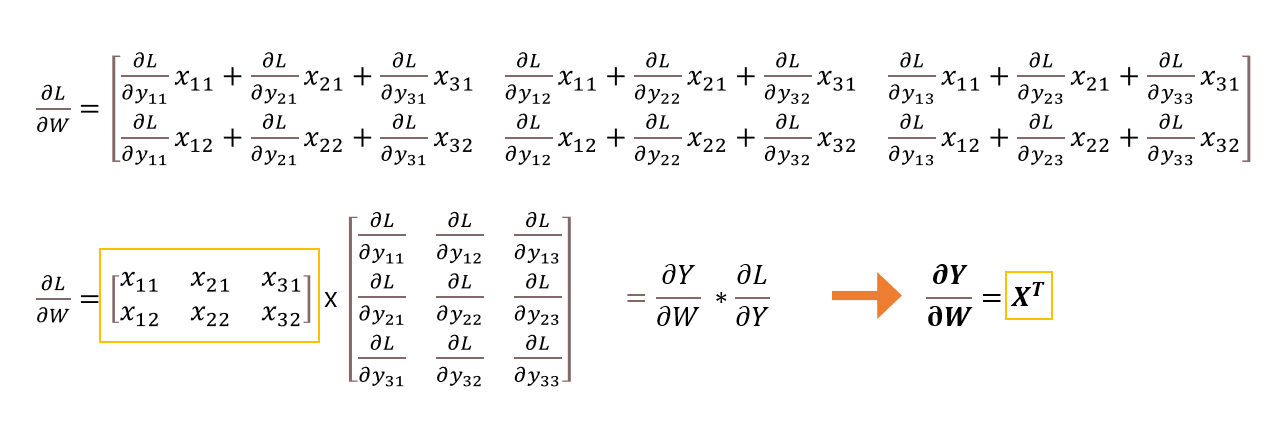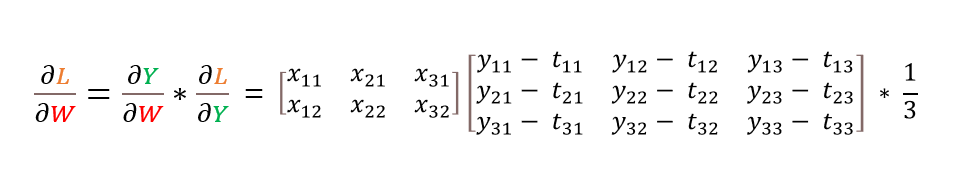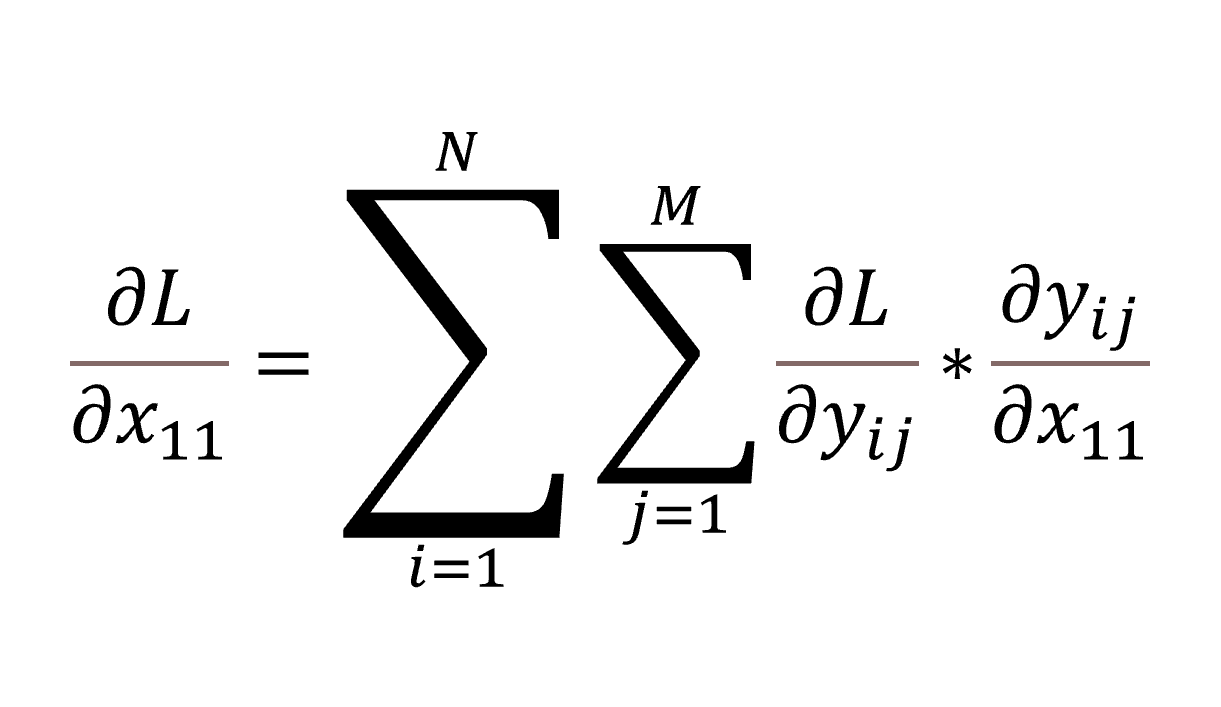
1. 연쇄법칙을 통한 곱셈형태 표현
이 포스팅은 "밑바닥부터 시작하는 딥러닝" 책을 공부하다가
𝜕L/𝜕W = 𝜕Y/𝜕W * 𝜕L/𝜕Y (연쇄법칙) = X.T * 𝜕L/𝜕Y
위 수식을 보고 이해가 안돼서 쓰기 시작한다. 왜 가중치 행렬로 손실함수를 미분하면 데이터 행렬 X의 전치행렬을 맨 앞에 곱하는 형태가 되는지?
이 글을 포스팅하는 순간의 나는 아직 다변수 미적분을 모른다. 그래서 행렬 수식을 이해할 수 있는데까지 풀어보고 이를 스칼라 단위의 계산그래프로 구현해 결과를 확인하고자 한다.
논의를 간단하게 하고자 활성화함수 등은 생략한 다중회귀분석 모형으로 진행하겠다. 어차피 오차역전파 구현 시 그대로 사용할 수 있다. 최종 손실함수는 MSE이다. (교차 엔트로피든 상관 없다.)
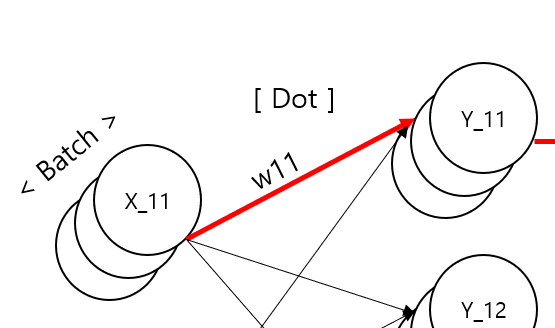
데이터 행렬 X는 (3 x 2) 행렬이다. 입력 데이터가 총 3개, 각 데이터는 2개의 특징을 갖는다. 배치처리를 고려한다.
가중치 행렬 W는 (2 x 3) 행렬이다. 열 값이 3임으로 Y(X * W) 행렬은 각 행마다 3개의 스칼라 출력이 나온다.
보통의 다중회귀분석이라면 W는 행렬이 아닌 열벡터로 주어지고, Y도 열벡터가 된다.
딥러닝 은닉층에서도 활용 가능하도록 W를 3개 열을 갖는 행렬로 정했다. Y 행렬에서 Y의 행들은 같은 위치의 X의 행들(각 데이터)에 대한 예측값인데, 이게 벡터로 나온다고 생각하면 된다.
은닉층을 위한 것 뿐 아니라, 다중회귀분석 이더라도
정답데이터가 one-hot 인코딩 방식 등등의 형태라면 적용될 수 있다.
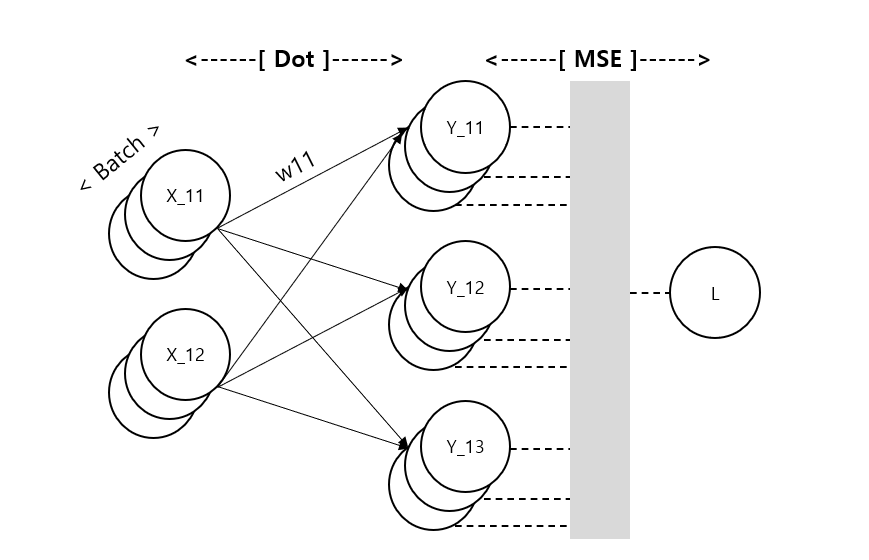
다중회귀분석의 신경망을 그려보았다. Dot 구간에서는 가중치 행렬 W와 행렬곱을 통해 Y가 되고 MSE 구간에서는 정답행렬 T와 Y의 각 행벡터 별 오차제곱합들을 평균내는 과정이다. 참고로 MSE 방식과 회귀분석에서 SSR 등의 개념으로 접근할 때의 방식은 표기에 약간의 차이가 있다. 1/2 를 곱하는 이유는 one-hot 인코딩에서 최대 오차값을 1로 맞추기 위함이다.
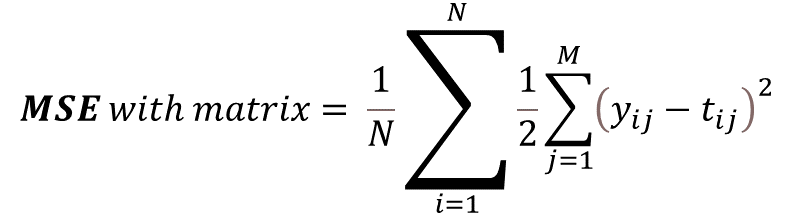
MSE는 입력이 벡터인가, 행렬인가에 따라 내부 식 표기가 약간 달라진다. 개념적으로 원소끼리의 차이의 제곱(오차제곱)을 서로 더하고, 평균을 냄으로 행렬이 들어가도 스칼라 값이 나온다. 앞서 언급한 것 처럼 다중회귀분석은 보통 y가 벡터 형태로 나오기 때문에 식이 다르다. 정답 원소가 벡터일 경우 오차 제곱합 후 평균값을 내기 위해 한번 더 합하는 과정이 필요하다.
오차역전파는 최종 스칼라 손실값 L을 출력하는 함수 MSE를 가중치행렬 W로 편미분하는 과정에서 연쇄법칙을 이용하게 된다. L이 값이자 손실함수라고 가정하자.
다음과 같이 곱셈형태로 분할하여 나타낼 수 있다. 주의할 점은 오른쪽으로 푸는게 아니라 왼쪽으로 풀어야 한다.
경사하강법을 위해 구해야할 것은 𝜕L/𝜕W 이고, 이는 가중치 행렬 W에 편미분 행렬을 element-wise로 뺄셈하여(학습률 곱하고) 구현하게 된다.
여기서 짚고 넘어가야 할 것은 분모중심 표현이다. 스칼라 함수를 벡터나 행렬로 미분할 때 그 결과값이 분모로 들어가는 백터나 행렬의 형태를 따르는 것이다.
분자에 스칼라 함수가 아니라 벡터나 행렬이면 전치 된다. 여튼 분모(분모중심 표현에서)의 shape으로 브로드캐스팅 되는 식 인것 같다. 스칼라/벡터, 벡터/스칼라, 스칼라/행렬, 행렬/스칼라, 벡터/벡터 까지는 브로드캐스팅으로 단순하게 2차원을 떠올릴 수 있는데 벡터/행렬, 행렬/행렬은 지금 포스팅 시점에선 모르겠다. 아마도 텐서곱, 야코비 행렬 등을 공부해야 하는것 같다. 후술하겠지만 사실 텐서단위로 올라갈 필요는 없다.
2. 손실함수와 X*W 의 편미분
하여튼 가중치 행렬 W에 그대로 요소별 뺄셈을 하기 때문에 분모중심 표현으로 시작해서 연쇄미분 식에 접근해보자.
MSE를 통해 행렬 Y가 들어오고, 내부적으로 정답행렬 T와 오차제곱합의 평균을 계산한다.
MSE(Y) = L 인 형태로 스칼라를 행렬로 미분하는 식이다. 이는 분모의 원소 배열로 브로드캐스팅 되어 간단하게 계산할 수 있다. 다음 단계로 넘어가자.
3. 행렬곱(X*W) 함수와 W의 편미분
이번에는 행렬의 원소가 행렬인 4차원 텐서? 같은 것이 되었다.
3-1. 원소별 편미분
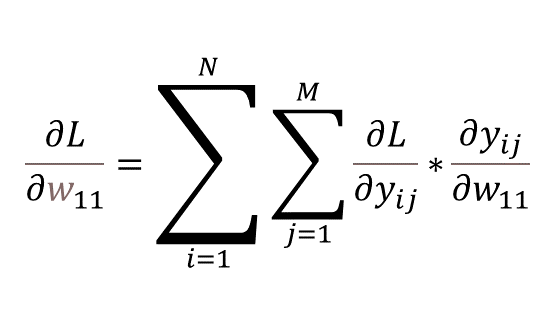
다행히 위의 summation 수식을 적용하면 역시 각 원소행렬의 모든 원소의 합으로 표현된다. (참고 블로그 - 1) 갑자기 왜 편미분 값들을 합하는지 의아할 수 있는데, L값을 계산하는 전체 다항식을 펼쳐보면 이해할 수 있다.
w11은 y11, y21, y31에만 각각 영향을 주기 때문에 편미분의 합이 되는 것이다. 위 그림의 마지막 줄을 보면 행렬 곱의 결과인데, 다항식을 편미분했을 땐 더하는 과정에서 스칼라가 나왔지만, 행렬의 원소를 모두 더하기 직전의 형태를 보이기 위해 행렬의 곱으로 표현해 보았다. 행렬 곱의 경우 1행을 제외하고 모두 0이고 이들을 다 더한 것이, 하나의 미분값 원소가 되는 것을 알 수 있다.
이 신경망 그림에서 y_11 의 밑에 포개진 것들은 y_21, y_31이다. 배치를 그려내고자 이런 그림이 되었다. 그럼 이제 가중치 행렬 W로 미분한 결과를 행렬로 다시 나타내보자.
드디어 결론에 도달했다.
4. 결론
사실 여기까지 오면서 다차원의 미적분의 지식이 필요한 것이 아니었다. 그저 마지막 손실값의 다항식을 기반으로 가중치 행렬의 원소들을 편미분하는 과정에서, 연쇄법칙으로 분해 시 행렬곱으로 나타나는 부분들은 그대로 나타내고, 텐서 형태가 될 경우 다항식을 참고하여 차원을 낮추는 덧셈을 통해 스칼라 값으로 바꾸어 주었던 것이다.
행렬곱으로 나타내는 이유는 컴퓨터 연산이 행렬곱에 특화될 수 있기 때문인 것으로 보인다. 결과적으로 마지막 손실함수와 평균의 과정에서 덧셈으로 차원이 줄어들기 때문에 가능한 것 같다.
다변수 미적분과 선형대수학을 깊게 공부하고 돌아오면 또 다르게 생각할지도 모르겠지만, 적어도 지금에선 이 결론이 최선이다. 행렬로 표현하다 차원이 늘어나면 최종 다항식에 맞게 줄인다. 표기법으로써의 행렬 응용이 맞는 말이다. (참고 블로그 - 2)
길고 긴 다항식의 결과로 나오는 마지막 손실값은 스칼라이고, 그 중간 중간을 연쇄법칙에 맞게 나누어 이를 행렬의 곱으로 표현되도록 한 것이다.
단순히 shape을 같게 한다던가, 적절히 조정해줘야 해서 전치행렬이 된다든가 하는 설명은 선형대수학도 잘 모르는 나한테 전혀 와닿지 않았는데, 이번에 깊게 생각해보면서 조금은 더 이해할 수 있었다. 연립방정식, 다항식을 벡터, 행렬의 곱으로 표현하고 역으로도 쉽게 떠올릴 수 있는 훈련이 필요한 것 같다.
다음 포스트는 실제로 스칼라 단위로 계산그래프를 구현하여 결과를 확인하겠다.