문제

프로그래머스: 정수를 나선형으로 배치하기

양의 정수 n이 매개변수로 주어집니다. n × n 배열에 1부터 n2 까지 정수를 인덱스 [0][0]부터 시계방향 나선형으로 배치한 이차원 배열을 return 하는 solution 함수를 작성해 주세요.

풀이

사용 언어: java

첫 번째 풀이

원리

전제: 1부터 $n^2$까지 반복문을 돌며 배열에 삽입한다. 다음과 같은 배열이 만들어진다고 했을 때, x는 행, y는 열을 나타내도록 했다.

2차원 배열은 총 4개의 변이 있으며, 나선형이므로 각 변마다 방향이 다르다.

• 첫 번째 변: x값 고정, y값 증가
• 두 번째 변: x값 증가, y값 고정
• 세 번째 변: x값 고정, y값 감소
• 네 번째 변: x값 감소, y값 고정

값이 채워지는 것과 테두리를 연관 지어 생각했다.

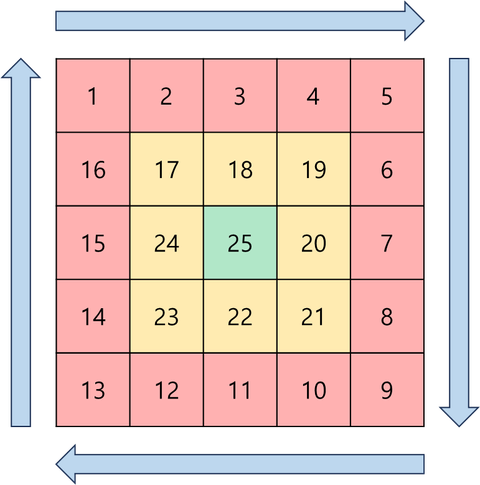
각 변을 차례로 돌며 첫 번째 테두리에 값을 모두 채운 다음, 다음 행(안쪽 행)으로 한 칸 내려가 다시 테두리를 채운다.

1. 맨 바깥쪽 테두리를 돌면서 값 삽입 → 붉은 색
2. 안쪽으로 한 칸 들어가 테두리를 돌면서 값 삽입 → 노란 색 (반복)

그리고 다음에 삽입할 값이 배열의 크기($n^2$)를 벗어나면 반복문을 멈춘다. → 초록 색

그러면 코드는 다음과 같아진다.

int 테두리를_돈_횟수 = 0;
int 삽입할_값 = 1;

while(삽입할_값 <= n^2) {

	// 첫 번째 변: x값 고정, y값 증가
	...

	// 두 번째 변: x값 증가, y값 고정
	...

	// 세 번째 변: x값 고정, y값 감소
	...

	// 네 번째 변: x값 감소, y값 고정
	...

	// 모든 변을 다 돌았으므로, 다음 테두리로 이동
	테두리를_돈_횟수 = 테두리를_돈_횟수 + 1;
}

각 변(방향)별 코드

이제 각 변을 따라 삽입할 값을 삽입하기 위한 코드를 작성한다. 먼저, 삽입할 숫자가 증가되어야 하므로 반복문을 사용한다.

첫 번째 변

x는 고정 값이고, y는 테두리까지 증가한다.

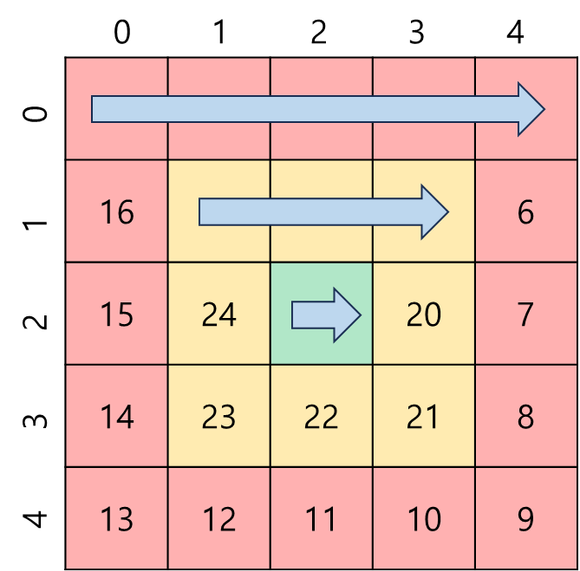
시작 인덱스

x는 테두리를 한 바퀴 다 돌고 나면, 아래 테두리로 한 칸 내려가야 하므로 1 증가한다. 이는 y도 마찬가지다. 안쪽 테두리로 이동하면서 시작 인덱스가 1 증가한다.

즉, 모든 테두리를 다 도는 것을 순환이라고 부른다면 x와 y의 값은 아래와 같다.

• 첫 번째 순환이라면 x = 0, y = 0
• 두 번째 순환이라면 x = 1, y = 1
• 세 번째 순환이라면 x = 2, y = 2

따라서, x와 y의 시작 인덱스 값을 테두리를_돈_횟수 로 초기화해야 한다.

종료 인덱스

첫 번째 변은 오른쪽 방향으로 이동한다. 즉, y의 인덱스가 증가한다. 그렇다면 어디까지 증가하는가?

y의 종료 인덱스도 테두리가 한 칸 줄어드므로 1씩 감소하는 걸 알 수 있다.

다시 말해, 한 번 순환을 돌 때 y의 시작 인덱스는 1 증가하고 종료 인덱스는 1 감소하는 것이다.

결과

for (y = cnt, x = cnt; y < (n-cnt); y++) {
		answer[x][y] = num++;
}

두 번째 변

x는 테두리까지 증가하고, y는 고정 값이다.

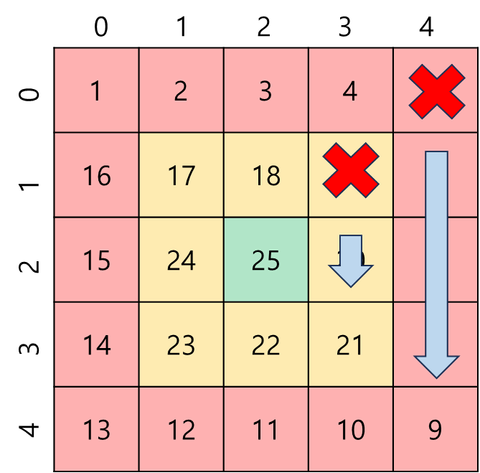
시작 인덱스

첫 번째 변을 돌면서 맨 위의 값(그림의 빨간 X 표시)은 이미 채워졌다. 즉, 그 다음 칸부터 채워야 한다.

x 는 고정 값이었으므로 테두리를_돈_횟수 에 1을 더하여 시작 위치를 맞춰 준다.

이 때, 첫 번째 변을 돌던 for 문이 y값을 하나 증가한 채로 종료했기 때문에 감소 시켜줘야 한다.

종료 인덱스

두 번째 변은 아래 방향으로 이동하므로 y의 인덱스가 감소한다. 첫 번째 변과 마찬가지로 순환을 마치면 테두리가 한 칸 좁아진다.

이제 제일 중요한 부분이 있다. 이렇게 최종 칸까지 채워버리면 다음 변을 돌 때 $1$을 더하거나 빼서 시작 위치를 맞춰 줘야 한다.

첫 번째 변은 최종 값을 삽입해야 하기 때문에 끝까지 채울 수 밖에 없었는데, 이후 변을 돌 때는 편하게 계산하기 위해서 두 번째 변은 끝에서 한 칸을 덜 채우게 했다.

따라서 종료 인덱스에 $-1$ 을 해줬다.

결과

for (x = cnt+1, y--; x < (n-1-cnt); x++) {
		answer[x][y] = num++;
}

세 번째 변

x는 고정 값이고, y는 테두리까지 감소한다.

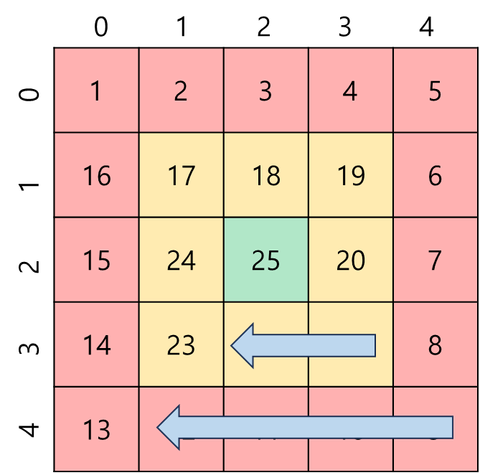
시작 인덱스

두 번째 변을 마치고 빠져나오면서 x의 값이 1 증가되는데, 이 인덱스가 다음에 채울 칸의 인덱스이므로 손대지 않는다.

y의 시작 인덱스는 마찬가지로 순회할 수록 좁아지므로 $n-테두리를돈횟수$ 이다. 여기에 앞서 말했든 다음 변을 쉽게 돌기 위해 끝에서 한 칸은 채우지 않았으므로 $-1$을 해준다.

💡 물론, y의 시작 인덱스를 선언해주지 않아도 된다. 이미 두 번째 변을 돌면서 해당 위치까지 갔기 때문이다.

종료 인덱스

테두리까지 가서 종료해야 하는데, 테두리의 인덱스는 테두리를 돈 횟수와 일치한다. 따라서, 테두리를 돈 횟수로 맞춰 준다.

결과

for (y = (n-1-cnt); y > cnt; y--) {
		answer[x][y] = num++;
}

네 번째 변

x는 테두리까지 감소하고, y는 고정 값이다.

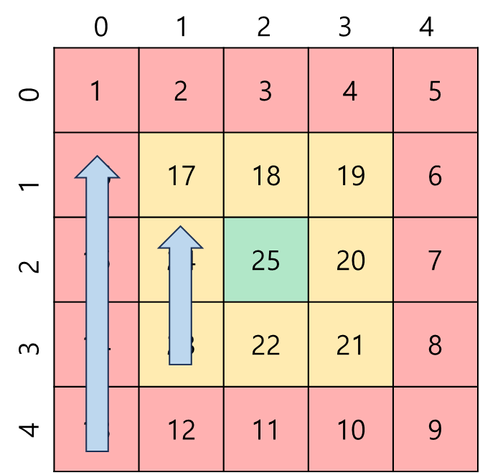
시작 인덱스

세 번째 변을 마치고 빠져나오면서 y의 값이 1 증가되는데, 이 인덱스가 다음에 채울 칸의 인덱스이므로 손대지 않는다.

x의 시작 인덱스 $n-테두리를돈횟수$ 에, 다음 변을 쉽게 돌기 위해 끝에서 한 칸은 채우지 않았으므로 $-1$을 해준다.

💡 세 번째 변을 돌면서 해당 위치까지 갔기 때문에 시작 인덱스를 지정하지 않아도 된다.

종료 인덱스

테두리까지 가서 종료해야 하는데, 테두리의 인덱스는 테두리를 돈 횟수와 일치한다. 따라서, 테두리를 돈 횟수로 맞춰 준다.

결과

for (x = (n-1-cnt); x > cnt; x--) {
		answer[x][y] = num++;
}

최종 코드

class Solution {
    public int[][] solution(int n) {
        int[][] answer = new int[n][n];

        int num = 1;
        int powNum = n*n;
        int cnt = 0, x = 0, y = 0;

        loop:
        while(num <= powNum) {

            // y 증가
            for (y = cnt, x = cnt; y < (n-cnt); y++) {
                if (num > powNum) break loop;
                answer[x][y] = num++;
            }

            // x 증가
            for (x = cnt+1, y--; x < (n-1-cnt); x++) {
                if (num > powNum) break loop;
                answer[x][y] = num++;
            }

            // y 감소
						// for (; y > cnt; y--) {
            for (y = (n-1-cnt); y > cnt; y--) {
                if (num > powNum) break loop;
                answer[x][y] = num++;
            }

            // x 감소
						// for (; x > cnt; x--) {
            for (x = (n-1-cnt); x > cnt; x--) {
                if (num > powNum) break loop;
                answer[x][y] = num++;
            }

            cnt++;
        }

        return answer;
    }
}

n=5 일 경우 로그를 찍어보면, 아래와 같이 변을 도는 것을 확인할 수 있다.

두 번째 풀이

제출하고 다른 사람의 코드를 봤는데, 놀랍게도 나처럼 이중 반복문을 쓰지 않고 작성할 수도 있었다. 이에 중첩문을 쓰지 않고, 다른 방식으로 다시 문제를 풀어봤다.

원리

전제: 1부터 $n^2$까지 반복문을 돌며 배열에 삽입한다. x는 행, y는 열을 나타내도록 했다.

기본 원리는 첫 번째와 거의 동일하다. 테두리를 한 번 돌고 안쪽 테두리로 진입하며, 이 한 번 도는 순환은 반복문의 시작부터 끝까지 한 번 가는 것을 말한다.

다른 점은 변 대신에 x와 y값이 증감하는 각 영역으로 계산해봤다.

• 첫 번째 구역에서는 y가 증가한다. y 범위는 0 → n-1
• 두 번째 구역에서는 x가 증가한다. x 범위는 0 → n-1
• 세 번째 구역에서는 y가 감소한다. y 범위는 n-1 → 0
• 네 번째 구역에서는 x가 감소한다. x 범위는 n-1 → 0

그리고 각 영역의 범위를 구하고, 해당 범위 안에 들어서면 영역의 규칙에 맞게 증감되도록 했다.

int 테두리를_돈_횟수 = 0;

for(int 삽입할_값 = 1; 삽입할_값 <= n^2; 삽입할_값++) {

	IF 첫 번째 영역: 
		y++;

	IF 두 번째 영역: 
		x++;

	IF 세 번째 영역: 
		y--;

	IF 네 번째 영역: 
		x--;

	// 모든 변을 다 돌았으므로, 안쪽 테두리로 이동
	첫번째_꼭지점 = 첫번째 + 1;
	마지막_꼭지점 = 마지막_꼭지점 - 1;
}

최종 코드

class Solution {
    public int[][] solution(int n) {
        int[][] answer = new int[n][n];
        
        int powNum = n*n;
        int x = 0, y = 0;
        int start = 0, end = n-1;
        
        for(int num = 1; num <= powNum; num++) {
            
            answer[x][y] = num;
        
            if (x == start && y < end) {
                y++;
            }
            else if (x < end && y == end) {
                x++;
            }
            else if (x == end && y > start) {
                y--;
            }
						else if (x > start + 1 && y == start) {
                x--;
            }
            
            if (x == start + 1 && y == start) {
                start++;
                end--;
            }
        }
        
        return answer;
    }
}

사실 방법은 한 가지가 더 있다.

다른 사용자가 푼 방법으로,

• 각 영역에서 증감하는 값을 direction 배열로 선언
• 방향이 전환되는 영역에 도달하면 배열의 인덱스를 조작하는 방식이다.

int dx[] = {0, 1, 0, -1};
int dy[] = {1, 0, -1, 0};
int direction = 0;

IF 방향이 전환되는 영역:
	direction = (direction + 1) % 4;

x = x + dx[direction];
y = y + dy[direction];

내 코드를 최적화하려고 조금씩 수정해가면서, 위 방식처럼 배열을 사용하자는 생각은 절대 못할 거란 걸 깨달았다.

그래서 최대한 내 힘으로 개선할 수 있을 때까지만 해보고, 위 방식은 코드를 읽어보기만 했다. 따라 적을 순 있겠지만 그렇다고 그게 내 생각이 되진 않으니까.