[알고리즘 스터디] Do it 알고리즘 코딩테스트 with Python #1

오예찬·2023년 9월 11일

Do it 알고리즘 스터디

목록 보기

1/18

알고리즘 스터디 시작

인프런을 통해 알고리즘을 공부한지 8개월 정도가 된 것 같다. 하지만 문제를 푸는 데 여전히 뭔가 중구난방식으로 푼다는 게 느껴진다. 정확한 근거를 가지고 푸는 게 아니라 일단 들이대고 보는 느낌? 스프링 스터디를 하다 알게 된 분의 조언으로 Do it 알고리즘 책으로 알고리즘의 유형을 제대로 확립하고자 한다. 그러면서 여태껏 미뤄두었던 백준 티어 올리기도 같이 해야겠다.

알고리즘 스터디을 혼자서 하는 건 아니고 학교 동기와 같이 진행하려고 한다. 아무래도 혼자 하면 잘 하다가도 어느 순간 놔버릴 것 같아 함께 하는 동료가 있으면 좋다. 진도는 책에서 추천하는 30일 코스로 진행할 예정이고 벨로그 포스팅도 30개 내외로 올릴 듯 하다. 다만 전번에 스프링 포스팅 같은 경우 나의 주관이 거의 없는 상태로 올렸는데 그러다 보니 너무 기계적으로 글을 올리는 것 같아 알고리즘 스터디부터는 점점 포스트에 내 색깔이 묻어날 듯하다.

어떤 알고리즘으로 풀어야 할까?

01-1 시간 복잡도 표기법 알아보기

시간 복잡도는 학교 이산수학 시간에 잠깐 배우고 시험까지 봤으나 그 당시 엄청난 벼락치기로 시험은 무난한 성적으로 끝낼 수 있었지만, 초초단기 기억에 저장하는 바람에 시험 본 다음 날로 완전히 잊어버렸다. 시간 복잡도는 3가지 유형으로 나뉜다.

빅-오메가(Ω(n)): 최선일 때(best case)의 연산 횟수를 나타낸 표기법

빅-세타(Θ(n)): 보통일 때(average case)의 연산 횟수를 나타낸 표기법

빅-오(O(n)): 최악일 때 (worst case)의 연산 횟수를 나타낸 표기법

시간 복잡도의 정의를 이해하기는 꽤 어려웠던 것 같은데 위의 정의는 직관적으로 보여 책의 저자에게 감사함을 느낀다. 예시 코드로 각 시간 복잡도의 횟수를 살펴 보자.

import random
findNumber = random.randrange(1, 101) # 1~100 사이 랜덤값 생성

for i in range(1, 101):
	if i == findNumber:
    	print(i)
        break

예시 코드의 시간 복잡도는 빅-오메가 표기법(Ω(n))의 시간 복잡도는 1번, 빅-세타 표기법(Θ(n))의 시간 복잡도는 N/2번, 빅-오 표기법(O(n))의 시간 복잡도는 N번이다.

그렇다면 코딩 테스트에선 어떤 시간 복잡도 유형을 사용해야 할까? 코딩 테스트에선 빅-오 표기법(O(n))을 기준으로 수행 시간을 계산하는 것이 좋다. 실제 테스트에선 1개의 테스트 케이스로 합격, 불합격으로 판단하는 것이 아닌 다양한 테스트 케이스를 모두 통과해야만 합격이 되기 때문에 시간 복잡도를 판단할 떄는 최악일 때를 염두에 두어야 한다.

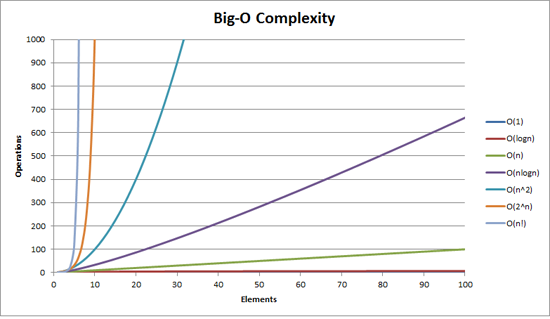
시간 복잡도는 데이터의 크기에 따라 수행 시간에 극명한 차이를 보이기 때문에 문제를 풀 때는 복잡도가 낮은 알고리즘을 써야 한다.

01-2 시간 복잡도 활용하기

연습 문제를 통해 시간 복잡도를 활용하는 법을 알아보자.

문제 000 수 정렬하기

시간 제한 : 2초

문제
N개의 수가 주어졌을 때, 이를 오름차순으로 정렬하는 프로그램을 작성하시오.

입력
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.

출력
첫째 줄부터 N개의 줄에 오름차순으로 정렬한 결과를 한 줄에 하나씩 출력한다.

예제 입력1
5
5
2
3
4
1

예제 출력 1
1
2
3
4
5

파이썬에선 2000만 번~1억 번의 연산을 1초의 수행 시간으로 예측할 수 있다. 하지만 문제를 풀 땐 항상 최악의 상황을 고려하므로 1초 = 2000만 번이라고 생각하면 된다.

연산 횟수 계산 방법

연산 횟수 = 알고리즘 시간 복잡도 n값에 데이터와 최대 크기를 대입하여 도출

알고리즘 적합성 평가

버블 정렬 = (1,000,000)^2 = 1,000,000,000,000 > 40,000,000 (부적합 알고리즘)
병합 정렬 = 1,000,000log2(1,000,000) = 약 20,000,000 < 40,000,000 (적합 알고리즘)

문제의 시간 제한은 2초이므로 연산은 4,000만 번 내로 수행되어야 한다. 버블 정렬은 1조 번의 연산을 수행하므로 부적합하지만 병합 정렬은 2,000만 번만 수행하므로 병합 정렬을 사용하는 것이 훨씬 유리하다는 것을 알 수 있다.

그렇다면 시간 복잡도를 바탕으로 코드 로직을 개선할 수 없을까? 이 답을 알기 위해선 먼저 코드의 시간 복잡도를 도출할 수 있어야 한다. 시간 복잡도를 도출하려면 다음 2가지 기준을 고려해야 한다.

상수는 시간 복잡도 계산에서 제외한다.

가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.

다음 코드를 보자

예제1 : 연산 횟수 = N

N = 10000
cnt = 1

for i in range(N)
	print("연산 횟수 " + str(cnt))
    cnt += 1

예제2 : 연산 횟수 = 3N

N = 10000
cnt = 1

for i in range(N)
	print("연산 횟수 " + str(cnt))
    cnt += 1
    
for i in range(N)
	print("연산 횟수 " + str(cnt))
    cnt += 1
    
for i in range(N)
	print("연산 횟수 " + str(cnt))
    cnt += 1

두 예제 코드의 연산 횟수는 3배 차이로 큰 차이 같지만 코딩 테스트에선 일반적으로 상수를 무시하므로 두 코드의 시간 복잡도는 O(n)으로 같다.

예제3 : 연산 횟수 = N^2

N=10000
cnt = 1

for i in range(N):
	for j in range(N):
    	print("연산 횟수" + str(cnt))
        cnt += 1

시간 복잡도는 가장 많이 중첩된 반복문을 기준으로 도출하기 때문에 이 코드에서는 이중 for문이 전체 코드의 시간 복잡도 기준이 된다. 만약 일반 for문이 10개 더 있다 하더라도 도출 원리 기준에 따라 시간 복잡도는 변화 없이 N^2으로 유지된다.

오예찬

안녕하세요. 반갑습니다.

다음 포스트