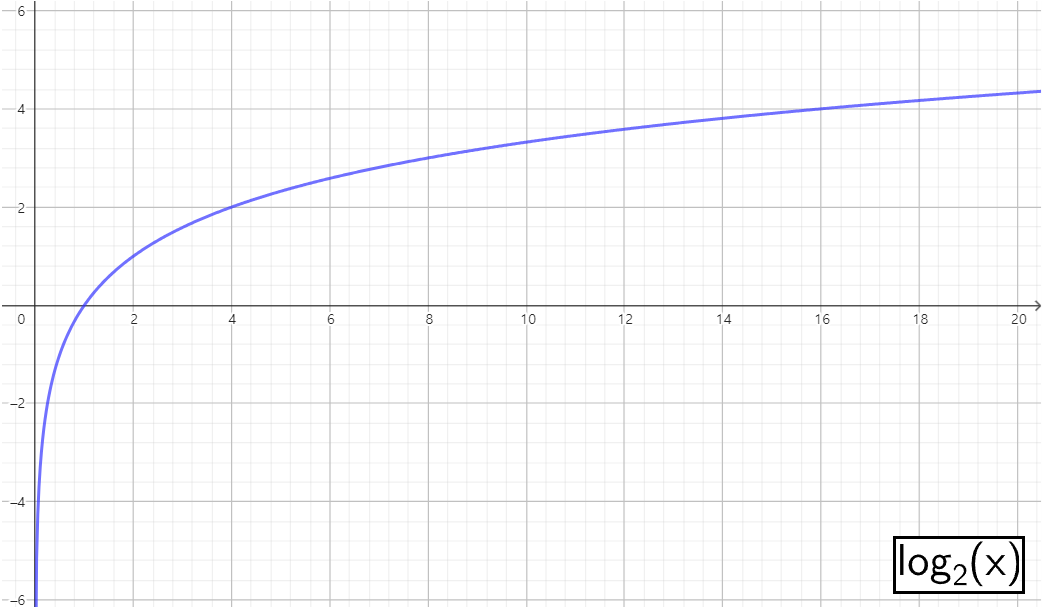
이진 시스템
당연하게 들리겠지만 이진수 시스템에서는 정보의 기본 단위가 비트(binary digit)이다. 따라서 정보 이론에서는 사건의 정보량을 비트 단위로 측정하는 것이 자연스럽다
로그 함수의 성질
logb(xy)=logb(x)+logb(y)
logb(xy)=ylogb(x)
위와 같은 로그함수의 성질로 정보의 독립적인 사건들의 정보량을 쉽게 합산할 수 있게 해준다.
사건의 정보량
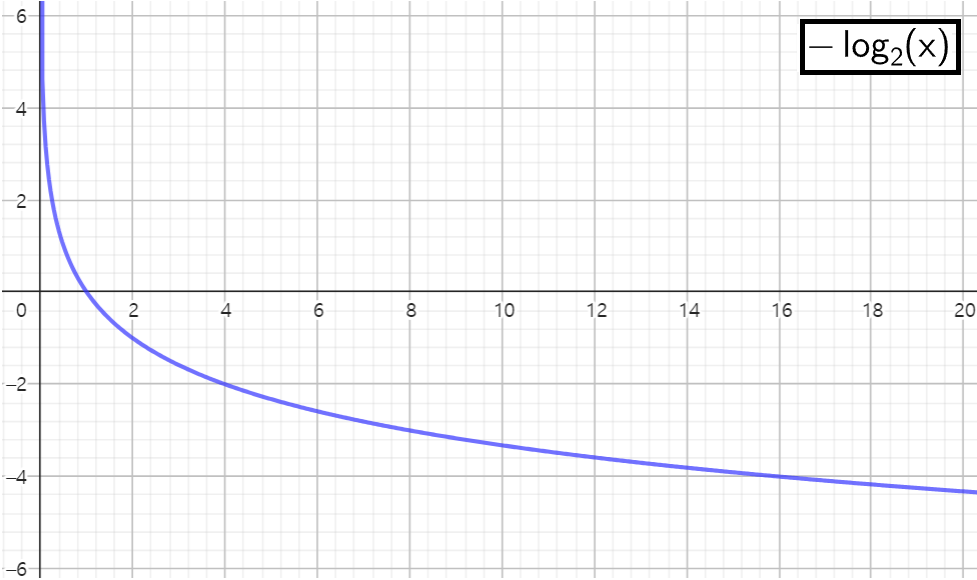
I(xi)=−log2P(xi)
- 사건이 자주 발생할수록 (확률이 높을수록) 그 사건의 정보량은 적다
- 사건이 드물게 발생할수록 (확률이 낮을수록) 그 사건의 정보량은 많다
정보 이론에서 사건의 정보량은 사건이 발생할 확률에 반비례한다. 즉, 희귀한 사건일수록 더 많은 정보를 제공한다고 보면 된다. 로그 함수를 사용하면, 확률이 낮을수록 정보량이 기하급수적으로 증가하는 특성을 갖게된다. 따라서 희귀한 사건의 정보량을 자연스럽게 더 많이 측정할 수 있다.
예를 들어, 공정한 동전을 던질 때:
- 앞면이 나올 확률 P(앞면)=0.5
- 정보량 I(앞면)=−log2(0.5)=1 bit
만약 사건의 확률이 0.25라면:
- 정보량 I(사건)=−log2(0.25)=2 bit
수학적 예시
1. 공정한 동전 던지기
- 사건의 확률 P(앞면)=0.5
- 정보량 I(앞면)=−log2(0.5)=−(−1)=1 bit
2. 주사위 던지기 (6개 면)
- 사건의 확률 P(1의 눈이 나올 확률)=61
- 정보량 I(1)=−log2(61)≈2.585 bit
Entropy, Cross-Entropy, K-L Divergence
하지만 머신러닝에서 log 의 밑은 2를 사용할 때도 있지만, 보통 자연상수 e 를 사용한다. 왜냐하면 e가 많은 자연현상과 수학적 모델링에서 더 자연스럽기 때문이다. 또한 밑을 자연상수로 했을 때, 자연로그라고 부른다. 기호는 loge 가 아니라 ln 을 사용하며 단위는 bit 가 아니라 nats 를 사용하게 된다.
Entropy
- 정보를 최적으로 인코딩하기 위해 필요한 bit 수
ex ) 일주일을 비트로 표현하면 7개의 비트가 아니라 3개의 비트가 필요
- 월(001), 화(010), 수(011), 목(100),금(101),토(110),일(111)
=> log2N
=> log27≈3
H(X)=−x∈X∑P(x)log2P(x)
혹은, =−x∈X∑P(x)lnP(x)
Cross-Entropy
- Classification 문제에서 loss function 으로 주로 사용
- 두 확률 분포간의 차이를 측정
- 모델의 예측이 실제 데이터와 얼마나 다른지를 정량화하기 위해 사용
H(P,Q)=−x∈X∑P(x)log2Q(x)
혹은, =−x∈X∑P(x)lnQ(x)
K-L Divergence
- 두 분포 차이를 줄이기 위해 KL-Divergence 를 최소화시킴
- 두 확률 분포 간의 차이를 비대칭적으로 측정
- P 와 Q 간의 크로스 엔트로피와 P의 엔트로피 차이를 계산하여 구할 수 있음
DKL(P∥Q)=x∈X∑P(x)log2Q(x)P(x)
혹은, =x∈X∑P(x)lnQ(x)P(x)
시나리오 기반 예시 ( 고양이와 강아지 데이터 )
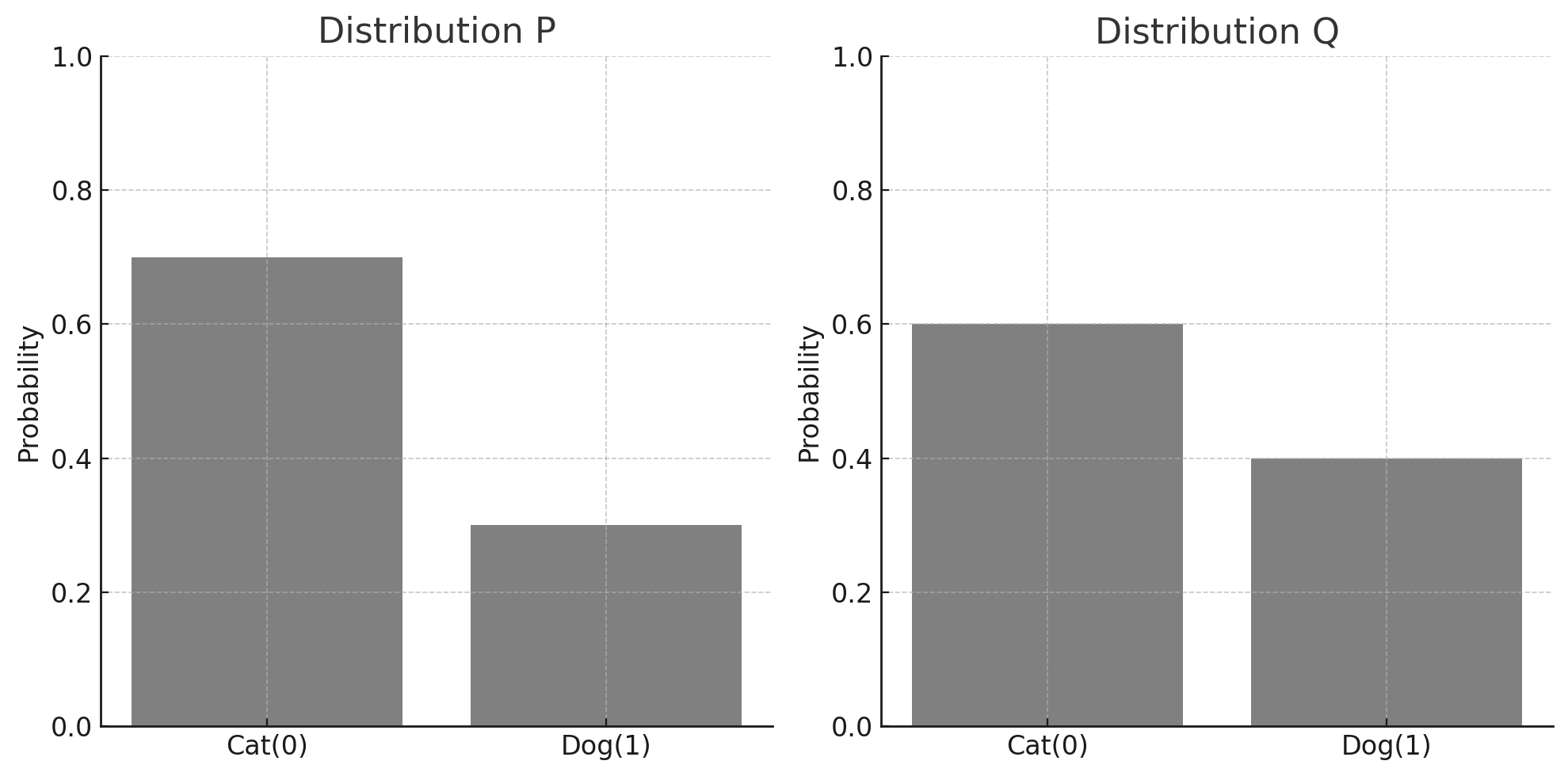
AI 회사에서 새로운 머신러닝 모델을 개발 중이다. 이 모델은 고양이와 강아지를 구분하는 이미지를 분류기이다. 실제 데이터에서 고양이 이미지가 70%, 강아지 이미지가 30%의 확률로 존재하지만 모델은 고양이 이미지를 60%, 강아지 이미지를 40%의 확률로 예측하고있다.
실제 확률 분포 P
- 고양이 : 70% ( 0.7 )
- 강아지 : 30% ( 0.3 )
P=[0.7,0.3]
예측 확률 분포 Q
- 고양이 : 60% ( 0.6 )
- 강아지 : 40% ( 0.4 )
Q=[0.6,0.4]
확률 분포 P 와 Q
| X | 0 | 1 |
|---|
| P(x) | 0.7 | 0.3 |
| Q(x) | 0.6 | 0.4 |
Entropy
밑이 2일 때,
H(P)=−[0.7log20.7+0.3log20.3]
H(P)≈−[0.7⋅(−0.51457)+0.3⋅(−1.73697)]
H(P)≈−(−0.3602−0.5211)
H(P)≈0.8813 bit
자연로그일 때,
H(P)≈−[0.7ln0.7+0.3ln0.3]
H(P)≈−[0.7⋅(−0.35667)+0.3⋅(−1.20397)]
H(P)≈−[−0.24967−0.36119]
H(P)≈0.6109 nats
Cross-Entropy
밑이 2일 때,
H(P,Q)=−[0.7log20.6+0.3log20.4]
H(P,Q)=−[0.7⋅(−0.73697)+0.3⋅(−1.32193)]
H(P,Q)=−(−0.5159−0.3966)
H(P,Q)=0.9125 bit
자연로그일 때,
H(P,Q)≈−[0.7ln0.6+0.3ln0.4]
H(P,Q)≈−[0.7⋅(−0.51083)+0.3⋅(−0.91629)]
H(P,Q)≈−[−0.35758−0.27489]
H(P,Q)≈0.6325 nats
K-L Divergence
밑이 2일 때,
DKL(P∥Q)=[0.7log20.60.7+0.3log20.40.3]
DKL(P∥Q)=[0.7log1.1667+0.3log0.75]
DKL(P∥Q)≈[0.7⋅0.22239+0.3⋅(−0.41503)]
DKL(P∥Q)≈0.15567−0.12451
DKL(P∥Q)≈0.0312 bit
자연로그일 때,
DKL(P∥Q)≈0.7ln(0.60.7)+0.3ln(0.40.3)
DKL(P∥Q)≈0.7ln1.1667+0.3ln0.75
DKL(P∥Q)≈0.7⋅0.15415+0.3⋅(−0.28768)
DKL(P∥Q)≈0.10791−0.08630
DKL(P∥Q)≈0.0216 nats