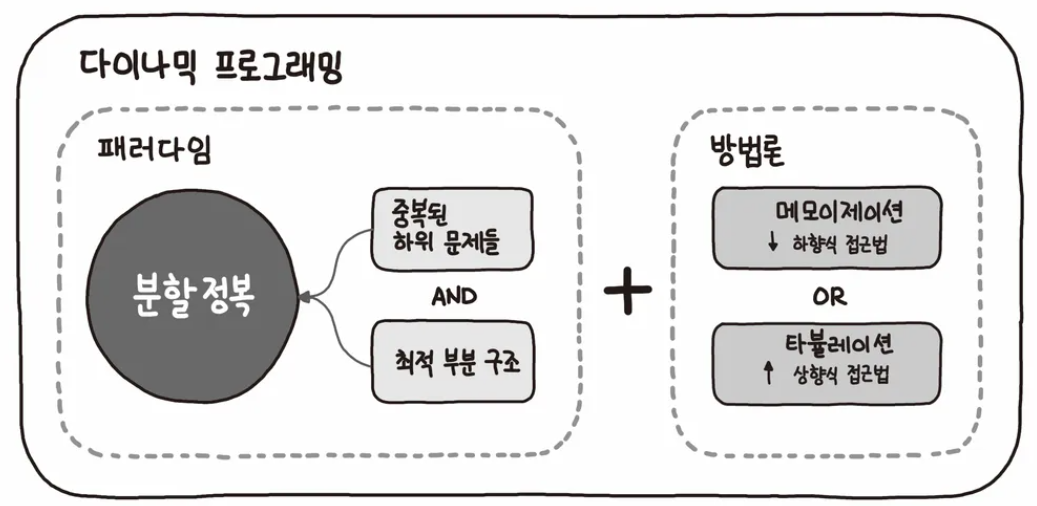
다이나믹 프로그래밍

다이나믹 프로그래밍은 복잡한 문제를 작은 [[하위 문제(sub-problems)]]로 나뉘어 해결하고, 그 결과를 저장[[Momoization (메모이제이션)]] 하여 나중에 동일한 하위 문제가 발생했을 때 빠르게 해결하는 알고리즘 설계 기법. 특히, 최적화 문제에 사용됨.

다이나믹 프로그래밍의 개념

1. [[하향식 (Top-Down) 접근법]] : 재귀를 사용하여 큰 문제를 작은 문제로 나눔
2. [[상향식 (Bottom-UP) 접근법]] : 작은 문제부터 시작하여 큰 문제를 해결
3. [[Momoization (메모이제이션)]] : 중복된 계산을 피하기 위해 이전에 계산한 값을 저장
4. [[상태 전이 (State Transition)]] : 하위 문제와 원래 문제 간의 관계를 찾음

장단점

장점

1. 시간복잡도 감소 : 중복 계산을 피하여 알고리즘의 속도를 높임
2. 코드의 재사용 : 작은 문제를 해결하는 코드를 큰 문제에도 적용할 수 있음

단점

1. 공간 복잡도 : [[Momoization (메모이제이션)]] 으로 인해 추가적인 메모리가 필요할 수 있음.
2. 코드 복잡성 : 다이나믹 프로그래밍을 이해하고 구현하기 복잡함.

사용방법

1. 문제 정의 : 문제를 해결하기 위해 작은 문제를 어떻게 나눌지 결정
2. 점화식 설정: 작은 문제들의 해답을 결합하여 큰 문제의 해답을 구할 수 있는 식을 만듬
3. 초기값 설정 : 재귀적으로 풀 때 기저 조건을 설정
4. 메모이제이션 : 중복되는 계산을 피하기 위해 한번 계산한 작은 문제의 해답을 저장해둠 보통 이를 위해 배열이나 딕셔너리를 사용

---

문제

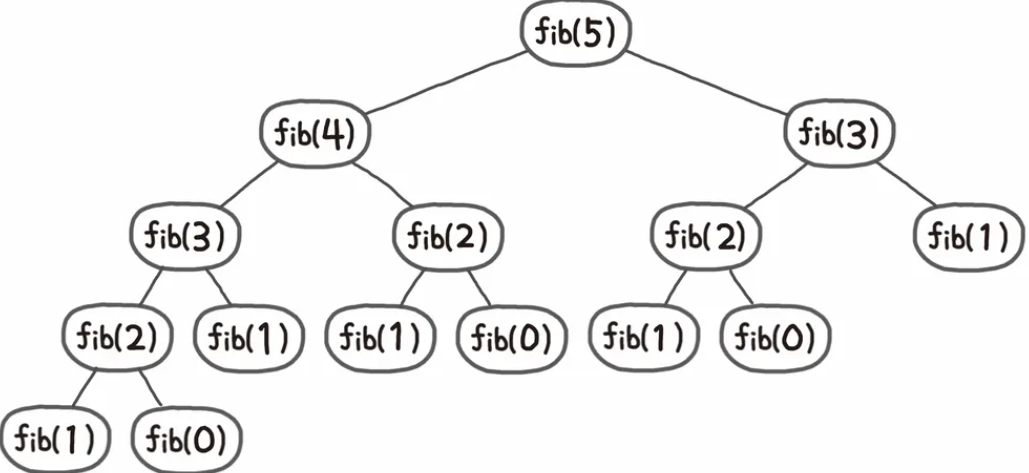
피보나치의 수 : https://www.acmicpc.net/problem/2748

[[하향식 (Top-Down) 접근법]]

def fibonacci(n, memo):
    if memo[n] is not None:
        return memo[n]
    
    memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo)
    return memo[n]

if __name__ == '__main__':
    user_input = int(input())
    
    memo = [0, 1] + [None] * (user_input - 1)
    print(fibonacci(user_input, memo))

재귀 함수를 호출하고 메모이제이션 하면 하향식

def fibonacci(n):
    memo = [0, 1] + [0] * (n - 1)  # 메모이제이션을 위한 배열 준비
    
    for i in range(2, n + 1):
        memo[i] = memo[i-1] + memo[i-2]  # 작은 문제의 해를 이용해 큰 문제 해결
        
    return memo[n]

배열에서 즉시 처리해주는 상향식

상향식과 하향식은 결과를 저장하고 재활용한다는 의미에서 아이디어가 동일하다.