➰힙(Heap)

[개념]

• 데이터에서 최댓값과 최솟값을 빠르게 찾기 위한 완전 이진 트리(Complete Binary Tree)
• 반정렬 상태(or 느슨한 정렬 상태, 약한 힙) : 부모자식간 우선순위만 고려, 형제간 X
• 힙트리 중복값 허용 : 이진트리 탐색은 중복 허용 X
• 우선순위 큐 : 우선순위 높은 데이터가 먼저 나감

[장점]

• 시간복잡도 감소 : 배열을 쓰는 O(n) 대신 O(logn) 시간 소요됨 (트리의 깊이만큼만 비교)
  • 모든 요소를 고려하여 우선순위 정렬X
  • 부모노드 우선순위가 항상 자녀노드 우선순위 앞섬

[종류]

• 최소 힙(min heap) / 최대 힙(max heap)
  
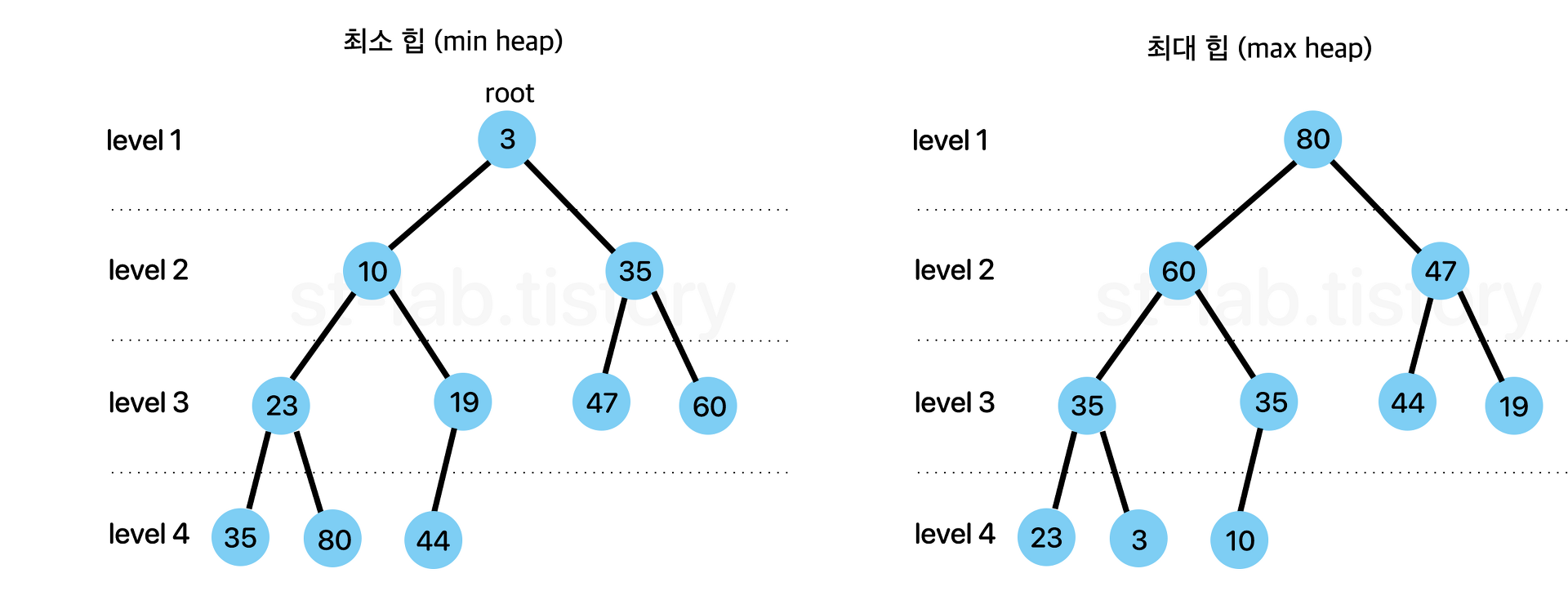
  • 최소 힙 : 부모노드 값 ≤ 자식노드 값
  • 최대 힙 : 부모노드 값 ≥ 자식노드 값

[동작 과정]

• 인덱스 부여
  • 왼쪽 자식노드 인덱스 = 부모 노드 인덱스 x 2 + 1
  • 오른쪽 자식노드 인덱스 = 부모 노드 인덱스 x 2 + 2
  • 부모노드 인덱스 = (자식 노드 인덱스 - 1) / 2

    ex)   1     - (부모)
    
         3   4   - (자식)

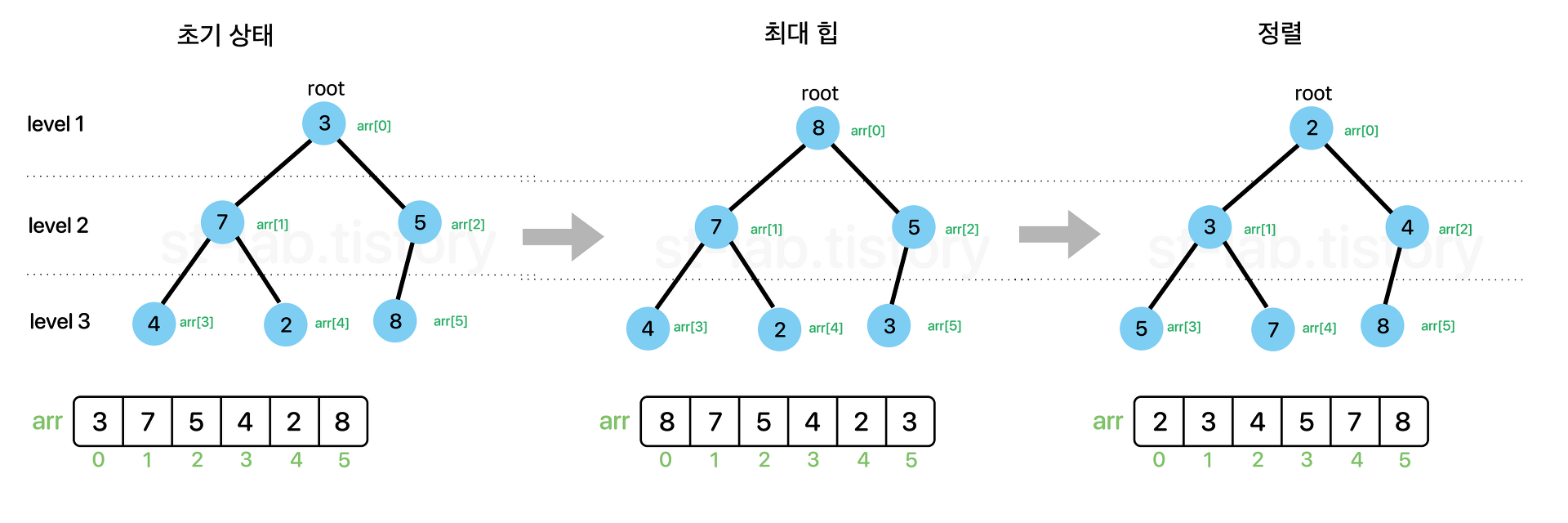
• 정렬
  • 삽입 : 일단 마지막 노드에 넣고, 부모 노드와 비교하며 힙 재구성
  • 삭제 : (최대 힙) 루트 노드 삭제, 빈 자리에 가장 마지막 노드를 가져온 뒤 힙 재구성
    

[코드]

• heapq 모듈
  • heappush(heap, item) : 힙 불변성 유지하며 heap에 item 추가
  • heappop(heap) : 힙 불변성 유지하며 heap에서 가장 작은 값 반환 (단, 힙 비어있을 시 에러 발생)

### 최소 힙 
import heapq

heap = []

for i in range(1, 6):
	heapq.heappush(heap, i)
	# heap = [1, 2, 3, 4, 5]

for i in range(5):
	print(heapq.heappop(heap))
	# 1 2 3 4 5 순으로 출력

### 최대 힙
import heapq

heap = []
values = [1, 5, 3, 2, 4]

for value in values:
	heapq.heappush(heap, -values)
	# heap = [-5, -4, -3, -1, -2] (최소 힙)

for i in range(5):
	print(-heapq.heappop(heap)) # heapq 최대 힙 따로 제공X, 부호 바꾸어 구현
	# 5, 4, 3, 2, 1 순으로 출력