키 교환 : Diffie-Hellman 알고리즘
.
.
대칭키 암호 -> 수신자와 송신자가 같은 키를 공유하고 있다는 전제가 필요
-> 키 교환(Key Exchange)가 이뤄져야 함
-> 키를 안전하게 공유할 수 없는 환경에서 대칭키 암호는 무용지물
공개 키 교환 알고리즘 -> 공개된 채널을 통해 키를 교환해도 외부인은 키를 알 수 없음
최초의 공개 키 교환 알고리즘 = Diffie-Hellman 키 교환 절차 (Diffie-Hellman key exchange protocol)
Diffie-Hellman Key exchange protocol 에 필요한 수학적 배경지식
- Square and multiply (모듈로 연산에서의 거듭제곱)
임의의 합동 항등식에 대해, 양변에 동일한 값을 곱해도 식은 성립
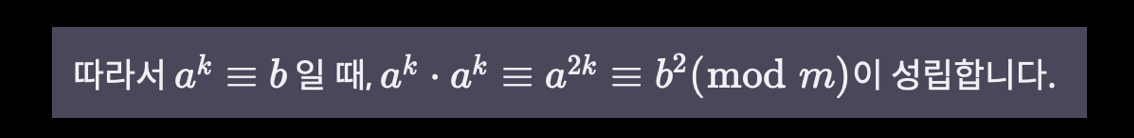
- 페르마의 소정리(Fermat’s Little Theorem)
소수 p와 정수 a에 대해 ap-1 ≡ 1(mod p) 성립 - 이산 로그 문제(Discrete Logarithm Problem)
자연수 a, m, 정수 b에 대해 ax ≡ b(mod m)을 만족하는 정수 x를 구하는 문제

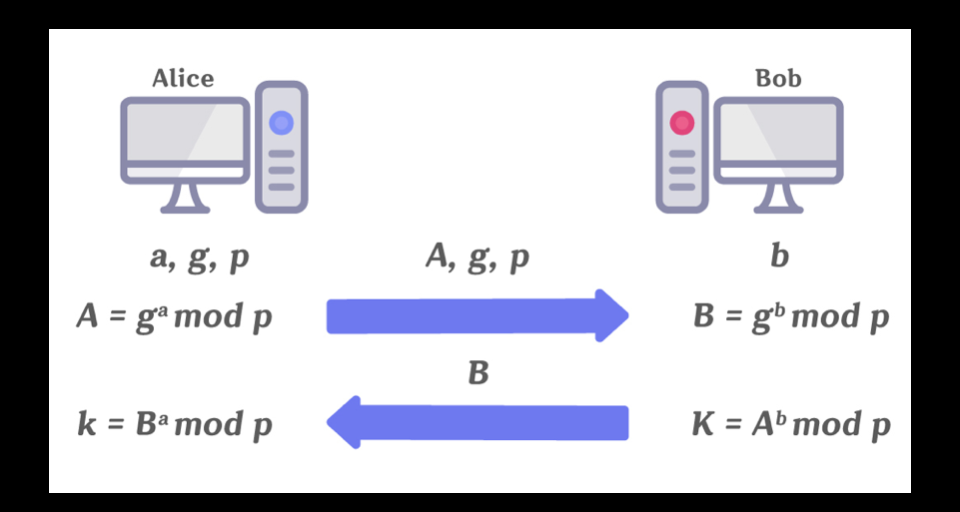
키 교환 절차
중간자 공격
수동적 공격 - 공격자가 통신에 개입하지 않음, 둘 사이의 통신 도청 외엔 아무것도 못함
능동적 공격 - 공격자가 통신에 직접 개입, 통신을 도청하며 중간에 데이터 위변조 가능
중간자 공격 - 능동적 공격에 해당
Diffie-Hellman key exchange protocol은 중간자 공격에 취약
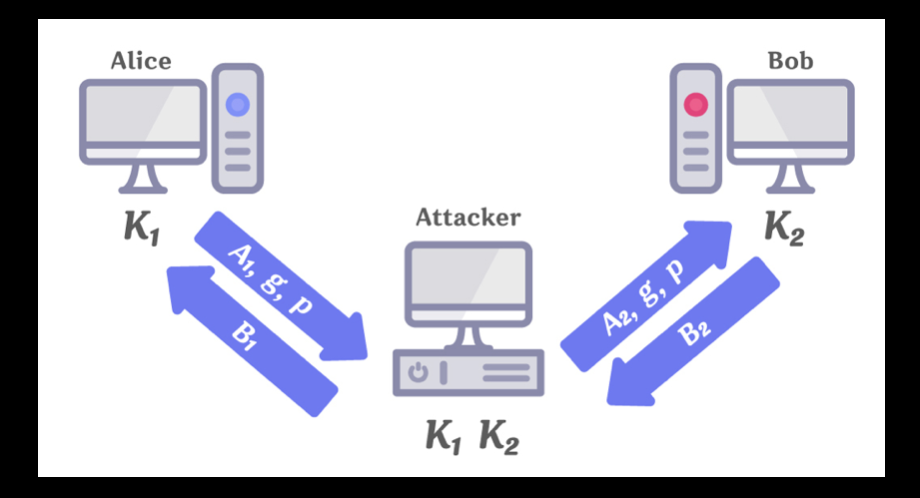
Alice가 Bob에게 키 교환 시도하면, 공격자는 이를 가로채 둘 모두와 키 교환 진행 -> alice는 K1 키를, bob이랑은 K2키 공유 -> alice는 bob과 k1을, bob은 alice와 k2 공유했다고 믿음 -> alice가 k1으로 암호화된 데이터를 전송하면 공격자는 복호화 한 뒤 k2로 다시 암호화해서 bob에게 보냄
