PWNME CTF QUALS 2025 - Easy Diffy, Square Power, My Zed, Mafia at the end 1, Mafia at the end 2
CTF

한국 시간대로는 매우 쉽지 않은 새벽 4시 시작 CTF 였어서 쉬운 크립토 문제들 쌀먹 많이 해버린 것 같다. with GPT 선생님.
Easy Diffy
Easy Diffy
Category: Crypto
Description: I managed to generate strong parameters for our diffie-hellman key exchange, i think my message is now safe.You’ll find a local flag hidden in the files we provided. Once you’ve got it, open a ticket on our Discord to receive your remote flag. Good luck and have fun!
Author : wepfen
Flag format: PWNME{.........................}
Tags: diffie-hellman
source.py, output.txt
from Crypto.Util.number import getPrime, long_to_bytes
from Crypto.Util.Padding import pad, unpad
from Crypto.Cipher import AES
from hashlib import sha256
import os
# generating strong parameters
flag = b"REDACTED"
p = getPrime(1536)
g = p-1
a = getPrime(1536)
b = getPrime(1536)
A = pow(g, a, p)
B = pow(g, b, p)
assert pow(A, b, p) == pow(B, a, p)
C = pow(B, a, p)
# Encrypting my message
key = long_to_bytes(C)
key = sha256(key).digest()[:16]
cipher = AES.new(key, AES.MODE_ECB)
ciphertext = cipher.encrypt(pad(flag, AES.block_size))
print(f"{p = }")
print(f"{g = }")
print("ciphertext =", ciphertext.hex())--------------------------------------------------------------------------
p = 1740527743356518530873219004517954317742405916450945010211514630307030225825627940655848700898186119703288416676610512180281414181211686282526701502342109420226095690170506537523420657033019751819646839624557146950127906808859045989204720555752289247833349649020285507405445896768256093961814925065500513967524214087124440421275882981975756344900858314408284866222751684730112931487043308502610244878601557822285922054548064505819094588752116864763643689272130951
g = 1740527743356518530873219004517954317742405916450945010211514630307030225825627940655848700898186119703288416676610512180281414181211686282526701502342109420226095690170506537523420657033019751819646839624557146950127906808859045989204720555752289247833349649020285507405445896768256093961814925065500513967524214087124440421275882981975756344900858314408284866222751684730112931487043308502610244878601557822285922054548064505819094588752116864763643689272130950
ciphertext = f2803af955eebc0b24cf872f3c9e3c1fdd072c6da1202fe3c7250fd1058c0bc810b052cf99ebfe424ce82dc31a3ba94f
Description
DH(Diffie-Hellman) 키 교환을 이용하는 문제
g = p - 1 이라서, 생성되는 공유 키 후보를 1 또는 p - 1 로 설정 가능
공유 키에서 유도된 키로 AES or XOR (일반적인 대칭키 암호화 알고리즘 시도) 하면 될 것 같음
문제를 봤을 때 공유 키를 SHA-256 해시 후에 앞 16바이트만 사용하여 AES 키를 생성하기 때문에 AEX-ECB로 복호화 후에 패딩을 제거해준다.
payload
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
from Crypto.Util.number import long_to_bytes
from hashlib import sha256
p = 1740527743356518530873219004517954317742405916450945010211514630307030225825627940655848700898186119703288416676610512180281414181211686282526701502342109420226095690170506537523420657033019751819646839624557146950127906808859045989204720555752289247833349649020285507405445896768256093961814925065500513967524214087124440421275882981975756344900858314408284866222751684730112931487043308502610244878601557822285922054548064505819094588752116864763643689272130951
ciphertext = bytes.fromhex("f2803af955eebc0b24cf872f3c9e3c1fdd072c6da1202fe3c7250fd1058c0bc810b052cf99ebfe424ce82dc31a3ba94f")
key1 = sha256(long_to_bytes(1)).digest()[:16]
key2 = sha256(long_to_bytes(p - 1)).digest()[:16]
cipher1 = AES.new(key1, AES.MODE_ECB)
cipher2 = AES.new(key2, AES.MODE_ECB)
try:
flag1 = unpad(cipher1.decrypt(ciphertext), AES.block_size)
if flag1.startswith(b"PWNME{"):
print("Flag:", flag1.decode())
except:
pass
try:
flag2 = unpad(cipher2.decrypt(ciphertext), AES.block_size)
if flag2.startswith(b"PWNME{"):
print("Flag:", flag2.decode())
except:
pass
공유키가 1일 경우, p-1일 경우로 나눠서 try if
PWNME{411_my_h0m13s_h4t35_sm411_Gs}
Square Power
Square Power
Category: Crypto
Description: Using p or N is outdated, let's square N!Author : lightender
Flag format: PWNME{.........................}
Files:
square-power.zip
Tags: Medium, Deffie-Hellman
challenge.py, output.txt
from Crypto.Util.number import getStrongPrime
from math import gcd
from random import randint
from typing import Tuple
from Crypto.Cipher import AES
from hashlib import sha256
flag = b"PWNME{xxxxxxxxxxxxxxxxxxxxxxxxx}"
def generate_primes() -> int:
p = getStrongPrime(512)
q = getStrongPrime(512)
while gcd(p*q, (p-1)*(q-1)) != 1:
p = getStrongPrime(512)
q = getStrongPrime(512)
return p*q
def generate_public_key() -> Tuple[int, int]:
n = generate_primes()
k = randint(2, n-1)
while gcd(k, n) != 1:
k = randint(2, n-1)
g = 1 + k * n
return n, g, k
n, g, k = generate_public_key()
a = randint(2, n-1)
b = randint(2, n-1)
A = pow(g, a, n*n)
B = pow(g, b, n*n)
secret_key = pow(B, a, n*n)
def encrypt(m: bytes, secret_key: int) -> str:
hash_secret_key = sha256(str(secret_key).encode()).digest()
cipher = AES.new(hash_secret_key, AES.MODE_ECB)
return cipher.encrypt(m).hex()
print(f"{n = }")
print(f"{g = }")
print(f"{k = }")
print(f"{A = }")
print(f"{B = }")
print(f'enc = "{encrypt(flag, secret_key)}"')--------------------------------------------------------------------------
n = 130480001264795511204952981970554765286628282097708497573805562495761746956689294837477924716000173700265689121058390655726461662172763702188805523675445230642476356316152454104476211773099930843629048798894397653741145611772970364363628025189743819724119397704649989182196725015667676292311250680303497618517
g = 14232999694821698106937459755169111250723143832548091913379257481041382160905011536064172867298828679844798321319150896238739468953330826850323402142301574319504629396273693718919620024174195297927441113170542054761376462382214102358902439525383324742996901035237645136720903186256923046588009251626138008729683922041672060805697738869610571751318652149349473581384089857319209790798013971104266851625853032010411092935478960705260673746033508293802329472778623222171537591292046922903109474029045030942924661333067125642763133098420446959785042615587636015849430889154003912947938463326118557965158805882580597710148
k = 109081848228506024782212502305948797716572300830339785578465230204043919222714279516643240420456408658167645175971167179492414538281767939326117482613367750888391232635306106151999375263906703485783436272382449557941704742019717763385971731987034043089865070488786181508175732060731733665723128263548176110391
A = 10331979810348166693003506393334562363373083416444082955583854323636220335613638441209816437198980825253073980493123573286927762799807446436773117670818921078297923733365129554252727963674496148945815529457095198387555733553703069705181377382893601879633657895337279524071439340411690401699779320407420258592904893010800421041848764790649945309236525529148459624417556599146885803882692326627657181584151248747924080070945415558421472606778565193931117263508570619290441914589981949634553417159683167906276897159926442471600725573380647253372071392282203683205441190912735696337884772579017885457286629133944441076065
B = 4081342267323018166249607688978380665241423816957875747125328810958590656153973787783246867777679461978030117454679495989870502705358238920918102708702013201363687875430336612386215884751792630402395947375495263771248401103245739000962715422458344125251671671250588124240486938525081520695571867300148511333511433839123962435025865462662009339451634433842267524048553313626315201481951251476302835595998914217740184369102003837614515913319042566394680732429410107620067602633793215206219823499602447575406162296590635685877032818801721681953430382920303700518722500790613216329394164889181089201919505288870098353385
enc = "abd9dd2798f4c17b9de4556da160bd42b1a5e3a331b9358ffb11e7c7b3120ed3"
Description
위의 easy diffy 문제는 소수 기반 Diffie-Hellman 이라면 이 문제는 RSA 기반 디피헬먼이다.
n = p q
k -> 2부터 n - 1 사이 랜덤 선택, n과 서로소 gcd(k,n) == 1 인 값
g = 1 + k n, mod n^2 생성 역할.
( g^n ≡ 1 (mod n^2) )
개인키 a, b
공개키 A, B
공유 비밀 키 S S = B^a mod n^2 , 대칭 암호 키로 사용됨
대칭 암호화 하여 enc 값을 얻고 있으므로 AES-EBC 암호화 방식 사용됨.
enc는 공유 비밀키로부터 나온 AES-256 키를 사용해 플래그를 ECB 방식으로 암호화 한 결과.
payload
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
from hashlib import sha256
n = 130480001264795511204952981970554765286628282097708497573805562495761746956689294837477924716000173700265689121058390655726461662172763702188805523675445230642476356316152454104476211773099930843629048798894397653741145611772970364363628025189743819724119397704649989182196725015667676292311250680303497618517
g = 14232999694821698106937459755169111250723143832548091913379257481041382160905011536064172867298828679844798321319150896238739468953330826850323402142301574319504629396273693718919620024174195297927441113170542054761376462382214102358902439525383324742996901035237645136720903186256923046588009251626138008729683922041672060805697738869610571751318652149349473581384089857319209790798013971104266851625853032010411092935478960705260673746033508293802329472778623222171537591292046922903109474029045030942924661333067125642763133098420446959785042615587636015849430889154003912947938463326118557965158805882580597710148
k = 109081848228506024782212502305948797716572300830339785578465230204043919222714279516643240420456408658167645175971167179492414538281767939326117482613367750888391232635306106151999375263906703485783436272382449557941704742019717763385971731987034043089865070488786181508175732060731733665723128263548176110391
A = 10331979810348166693003506393334562363373083416444082955583854323636220335613638441209816437198980825253073980493123573286927762799807446436773117670818921078297923733365129554252727963674496148945815529457095198387555733553703069705181377382893601879633657895337279524071439340411690401699779320407420258592904893010800421041848764790649945309236525529148459624417556599146885803882692326627657181584151248747924080070945415558421472606778565193931117263508570619290441914589981949634553417159683167906276897159926442471600725573380647253372071392282203683205441190912735696337884772579017885457286629133944441076065
B = 4081342267323018166249607688978380665241423816957875747125328810958590656153973787783246867777679461978030117454679495989870502705358238920918102708702013201363687875430336612386215884751792630402395947375495263771248401103245739000962715422458344125251671671250588124240486938525081520695571867300148511333511433839123962435025865462662009339451634433842267524048553313626315201481951251476302835595998914217740184369102003837614515913319042566394680732429410107620067602633793215206219823499602447575406162296590635685877032818801721681953430382920303700518722500790613216329394164889181089201919505288870098353385
enc_hex = "abd9dd2798f4c17b9de4556da160bd42b1a5e3a331b9358ffb11e7c7b3120ed3"
enc_bytes = bytes.fromhex(enc_hex)
a = ((A - 1) // (k * n)) % n
S = pow(B, a, n * n)
key = sha256(str(S).encode()).digest()
cipher = AES.new(key, AES.MODE_ECB)
decrypted_bytes = cipher.decrypt(enc_bytes)
flag = unpad(decrypted_bytes, AES.block_size).decode()
print(flag)
S 복원 : 일반적인 Diffie-Hellman이라면 S를 구하려면 한 쪽의 비밀키(a 또는 b)가 필요하지만, g = 1 + kn의 구조 때문에 공개값으로부터 비밀 지수를 구할 수 있다.
A = 1 + akn (mod n^2)이므로, a = (A-1/kn) * (mod n) 로 a 값 계산 가능
복호화 : A에서 개인키 a 계산 -> B^a mod n^2 로 공유 비밀키 S 계산 -> S 를 SHA-256 해시하여 AES 키 생성 -> AES-ECB 복호화
PWNME{Thi5_1s_H0w_pAl1ier_WorKs}
My Zed
My Zed
Category: Crypto
Description: Tried to make an opensource zedencrypt in 2 weeks but i got doubts about it ...Author : wepfen
Flag format: PWNME{.........................}
Files:
my_zed.zip
Tags: AES, Easy
Description
지피티의 한 달에 10번 사용할 수 있는 '심층 리서치' 기능이 95%는 풀어줌
(어케했음?ㄷㄷ)
앞으로 씨텦 문제에 ai로 풀리는지 더블검증도 들어갈듯
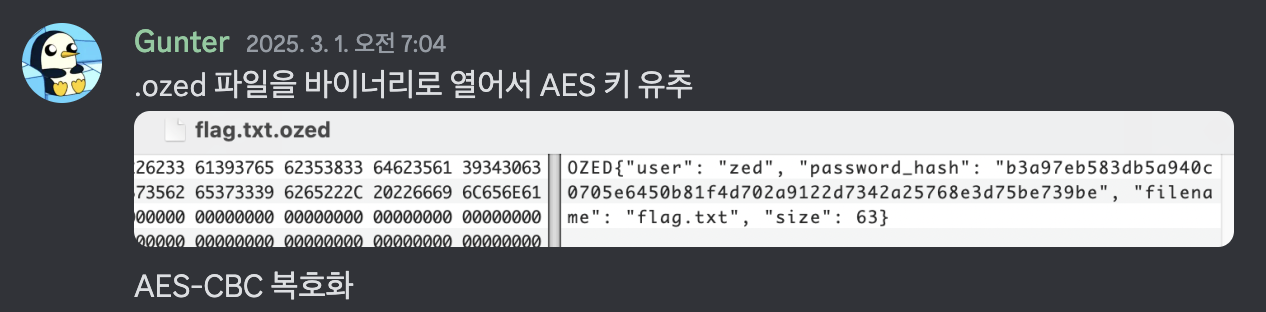
flag.txt.ozed 파일을 hex fiend로 열어서 메타데이터에서 password_hash 값 발견 -> AES 키 유추
from hashlib import sha256
import os
def xor(a: bytes, b: bytes) -> bytes:
return bytes(x^y for x,y in zip(a,b))
class AES_CBC_ZED:
def __init__(self, user, password):
self.user = user
self.password = password
self.derive_password()
self.generate_iv()
def encrypt(self, plaintext: bytes):
iv = self.iv
ciphertext = b""
ecb_cipher = AES.new(key=self.key, mode=AES.MODE_ECB)
for pos in range(0, len(plaintext), 16):
chunk = plaintext[pos:pos+16]
# AES CFB for the last block or if there is only one block
if len(plaintext[pos+16:pos+32]) == 0 :
#if plaintext length <= 16, iv = self.iv
if len(plaintext) <= 16 :
prev=iv
# else, iv = previous ciphertext
else:
prev=ciphertext[pos-16:pos]
prev = ecb_cipher.encrypt(prev)
ciphertext += xor(chunk, prev)
# AES CBC for the n-1 firsts block
elif not ciphertext:
xored = bytes(xor(plaintext, iv))
ciphertext += ecb_cipher.encrypt(xored)
else:
xored = bytes(xor(chunk, ciphertext[pos-16:pos]))
ciphertext += ecb_cipher.encrypt(xored)
return iv + ciphertext
def decrypt(self, ciphertext: bytes):
# TODO prendre un iv déjà connu en paramètre ?
plaintext = b""
ecb_cipher = AES.new(key=self.key, mode=AES.MODE_ECB)
iv = ciphertext[:16]
ciphertext = ciphertext[16:]
for pos in range(0, len(ciphertext), 16):
chunk = ciphertext[pos:pos+16]
# AES CFB for the last block or if there is only one block
if len(ciphertext[pos+16:pos+32]) == 0 :
#if plaintext length <= 16, iv = self.iv
if len(ciphertext) <= 16 :
prev=iv
# else, iv = previous ciphertext
else:
prev=ciphertext[pos-16:pos]
prev = ecb_cipher.encrypt(prev)
plaintext += xor(prev, chunk)
# AES CBC for the n-1 firsts block
elif not plaintext:
xored = ecb_cipher.decrypt(chunk)
plaintext += bytes(xor(xored, iv))
else:
xored = ecb_cipher.decrypt(chunk)
plaintext += bytes(xor(xored, ciphertext[pos-16:pos]))
return plaintext
def derive_password(self):
for i in range(100):
self.key = sha256(self.password).digest()[:16]
def generate_iv(self):
self.iv = (self.user+self.password)[:16]
위 aes_cbc_zed.py 코드를 보면 AES-CBC + 마지막 블록 CFB 변형 사용
IV 생성 방식이 "zed" + 패스워드 일부 포함 이라서 IV가 패스워드 일부를 노출하고 있음
Payload
import json
import zlib
from hashlib import sha256
from Crypto.Cipher import AES
with open("flag.txt.ozed", "rb") as f:
data = f.read()
meta_json = data[4:304].decode().strip("\x00")
meta = json.loads(meta_json)
password_hash = bytes.fromhex(meta["password_hash"])
aes_key = password_hash[:16]
enc_data = zlib.decompress(data[304:])
iv, ciphertext = enc_data[:16], enc_data[16:]
cipher = AES.new(aes_key, AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
print(plaintext.decode().strip())
password_hash 값에서 AES키 (16바이트) 추출
IV + 암호문 분리
AES-CBC 복호화 수행
PWNME{49e531f28d1cedef03103af6cec79669_th4t_v3Ct0r_k1nd4_l3aky}
Mafia at the end 1
Mafia at the end 1
Category: Misc
Description: You're an agent, your unit recently intercepted a mob discussion about an event that's going to take place on August 8, 2024. You already know the location, though. A password for the event was mentioned. Your job is to find it and return it so that an agent can go to the scene and collect evidence.Note : The contract is deployed on sepolia network
Authors : wepfen, teazer
Flag format: PWNME{.........................}
Files:
Mafia_at_the_end_of_the_block_1.zip
Tags: Blockchain, Network, Easy
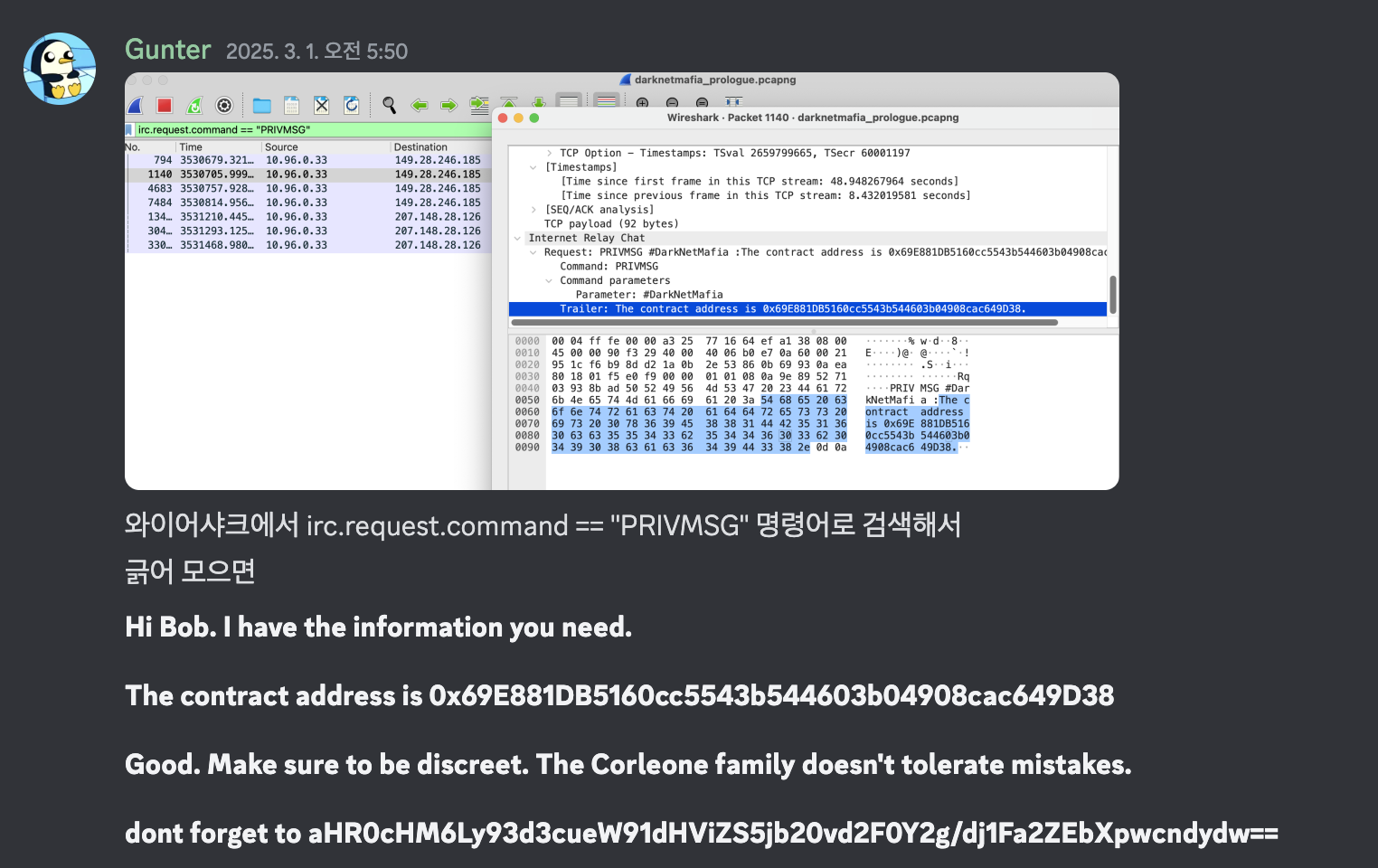
+) irc = internet Relay Chat. 채팅을 위한 텍스트 기반 프로토콜
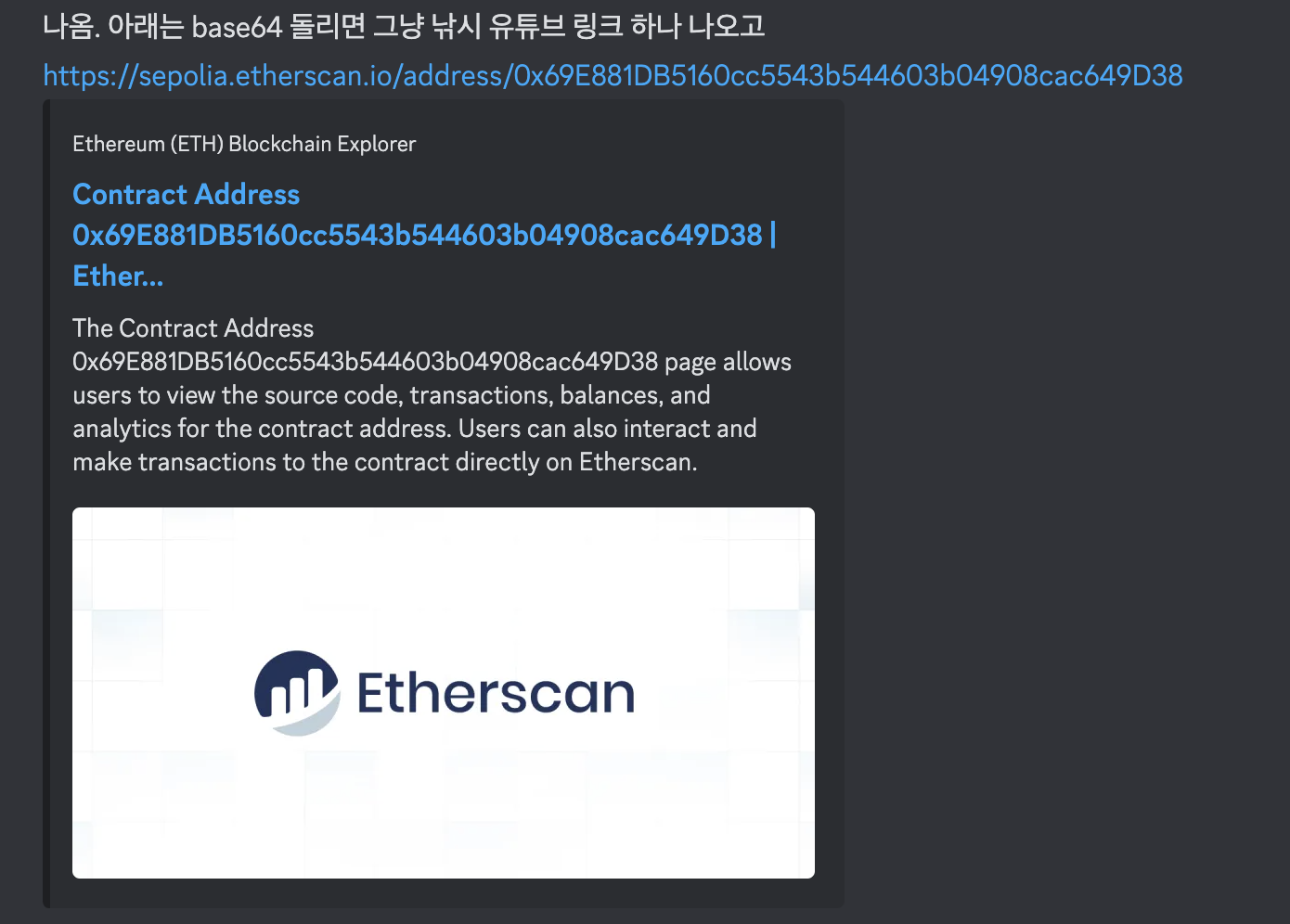
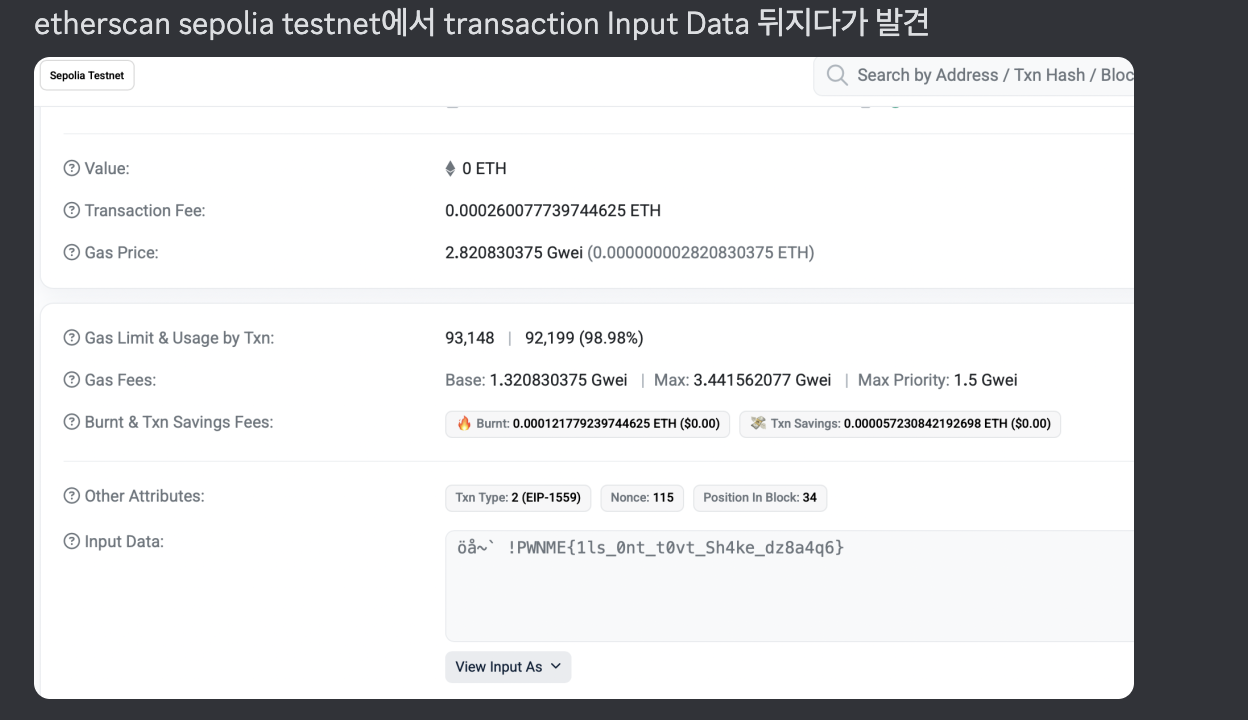
PWNME{1ls_0nt_t0vt_Sh4ke_dz8a4q6}
Mafia at the end 2
Mafia at the end 2
Category: Misc
Description: You're in the final step before catching them lacking. Prove yourself by winning at the casino and access the VIP room !But remember, the house always win.
Note : To connect to the casino with Metamask, we recommend you to use another browser and a "trash" MetaMask wallet to avoid some weird behavior.
Author : Wefpen, Tzer
Flag format: PWNME{.........................}
Connect : https://mafia2.phreaks.fr/ & `nc mafia2.phreaks.fr 10020
Files:
Mafia_at_the_end_of_the_block_2.zip
Tags: Medium, Blockchain
Casino.sol, Setup.sol, mafia.py
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.26;
contract CasinoPWNME {
bool public isWinner;
uint256 public multiplier = 14130161972673258133;
uint256 public increment = 11367173177704995300;
uint256 public modulus = 4701930664760306055;
uint private state;
constructor (){
state = block.prevrandao % modulus;
}
function checkWin() public view returns (bool) {
return isWinner;
}
function playCasino(uint number) public payable {
require(msg.value >= 0.1 ether, "My brother in christ, it's pay to lose not free to play !");
PRNG();
if (number == state){
isWinner = true;
} else {
isWinner = false;
}
}
function PRNG() private{
state = (multiplier * state + increment) % modulus;
}
},
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.26;
import {CasinoPWNME} from "./Casino.sol";
contract Setup {
CasinoPWNME public casino;
constructor() {
casino = new CasinoPWNME();
}
function isSolved() public view returns (bool) {
return casino.checkWin();
}
,
multiplier = 14130161972673258133
increment = 11367173177704995300
modulus = 4701930664760306055
current_state = int("0x063f7662ffa196f9", 16)
next_state = (multiplier * current_state + increment) % modulus
print(f"next state 값 : {next_state}")
Description
casino.sol엔 CasinoPWNME 라는 컨트랙트가 존재
isWinner : 사용자가 승리했는지 저장하는 public boolean 변수
playCasino : 최소 0.1ETH 베팅해야함. 내부적으로 PRNG() 호출해 state 값 업데이트. 입력한 number가 state와 같으면 isWinner = true
PRNG() : LCG ( Linear Congruential Generator ) 방식으로 난수 생성
- state의 초기값이 block.prevrandao % modulus로 설정됨 → 특정 블록에서 prevrandao 값을 가져와서 예측 가능.
- PRNG()의 선형 합동 생성기(LCG) 식을 이용해 다음 state 값을 예측할 수 있음.
- 예측한 state 값을 playCasino()에 입력하여 승리 조건을 충족시키면 isWinner가 true가 됨.
Payload
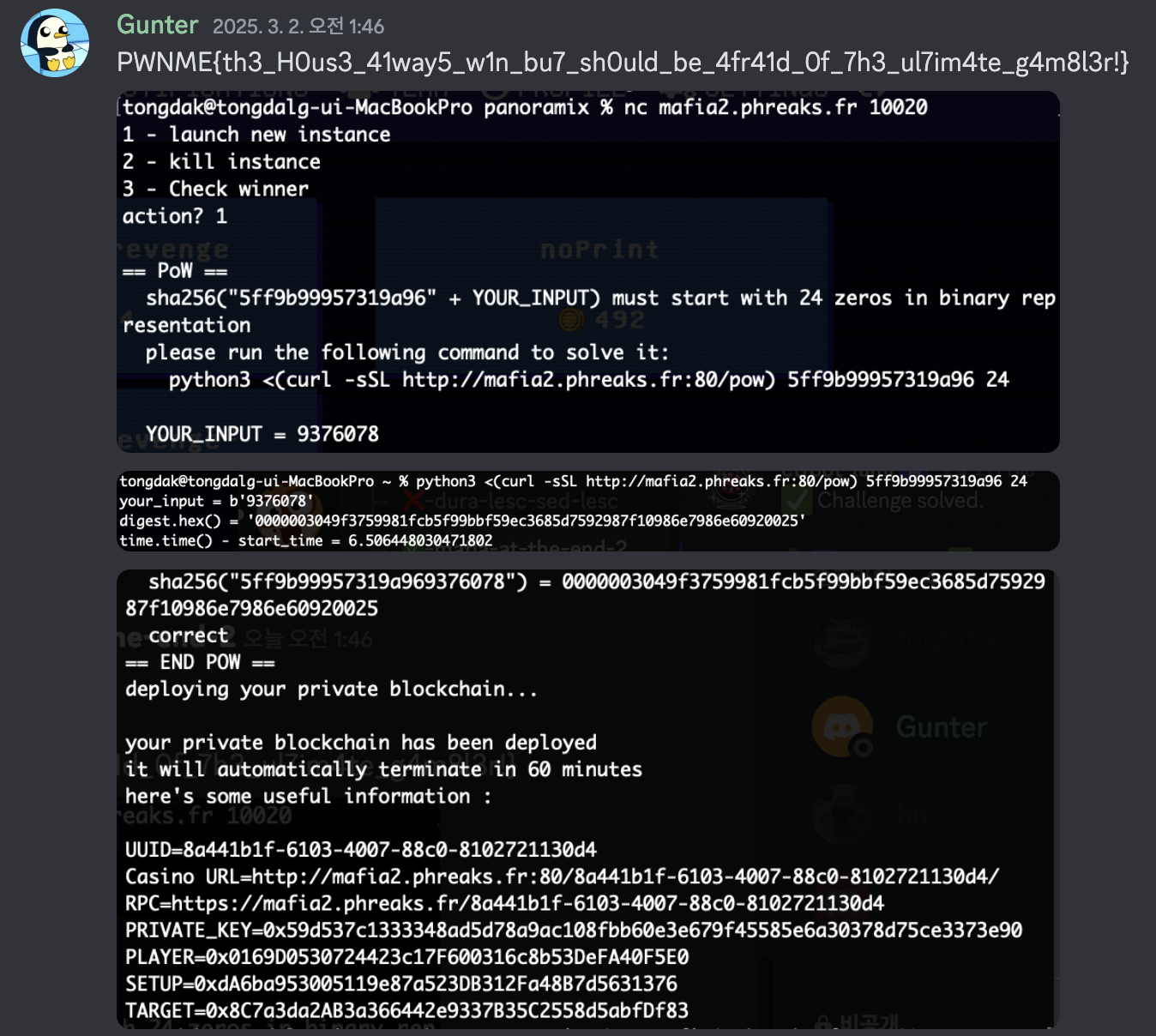
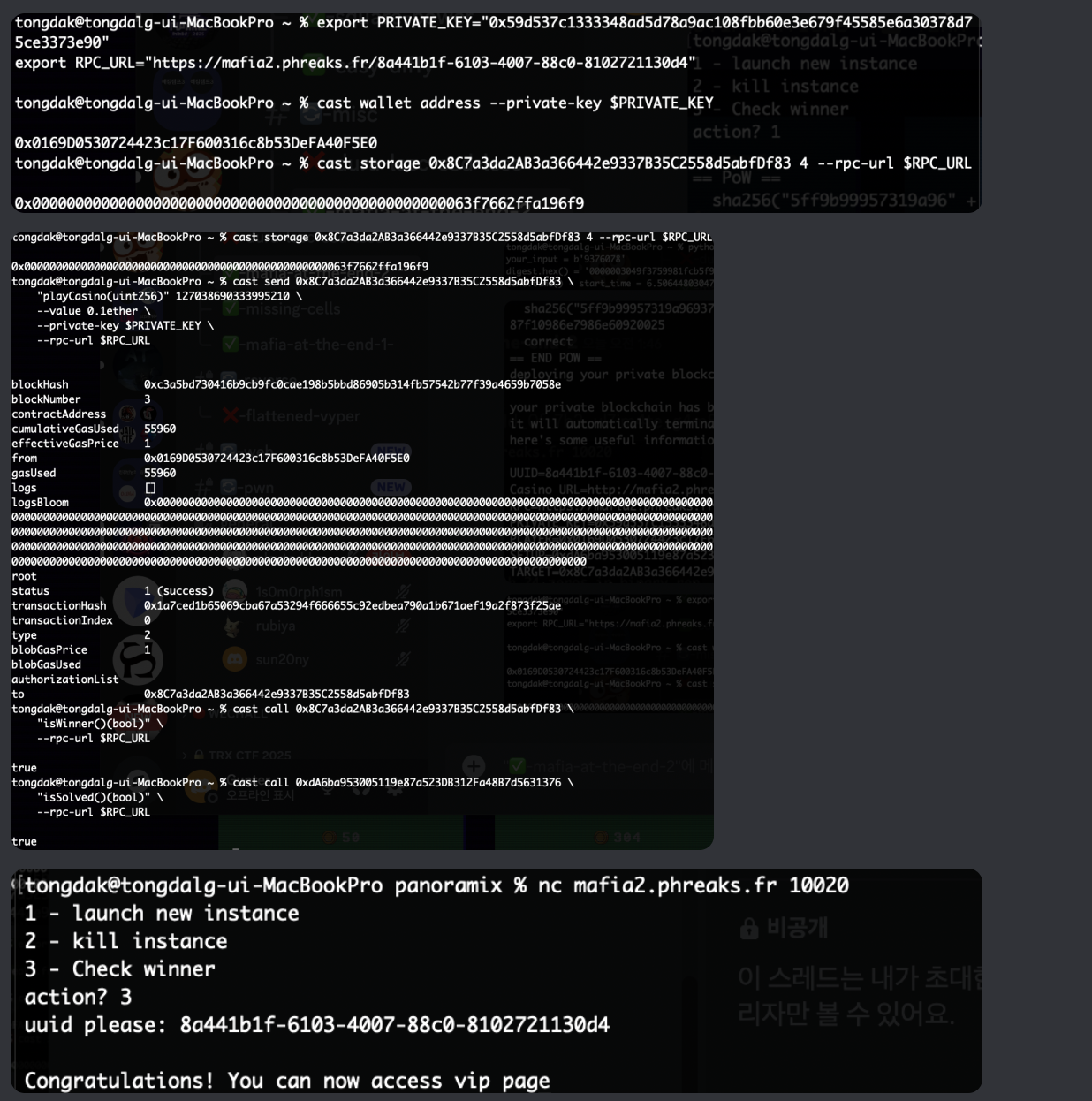
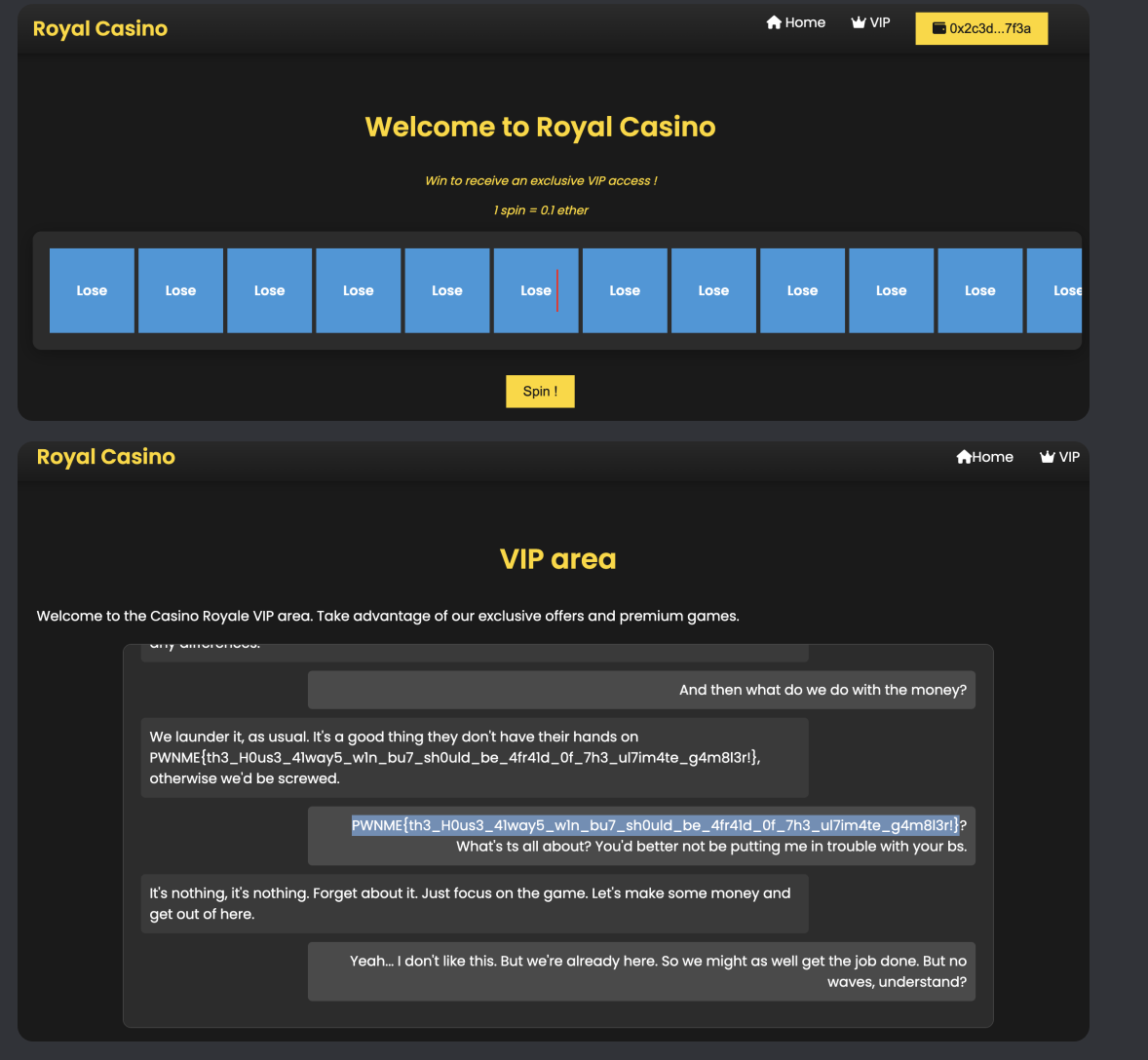
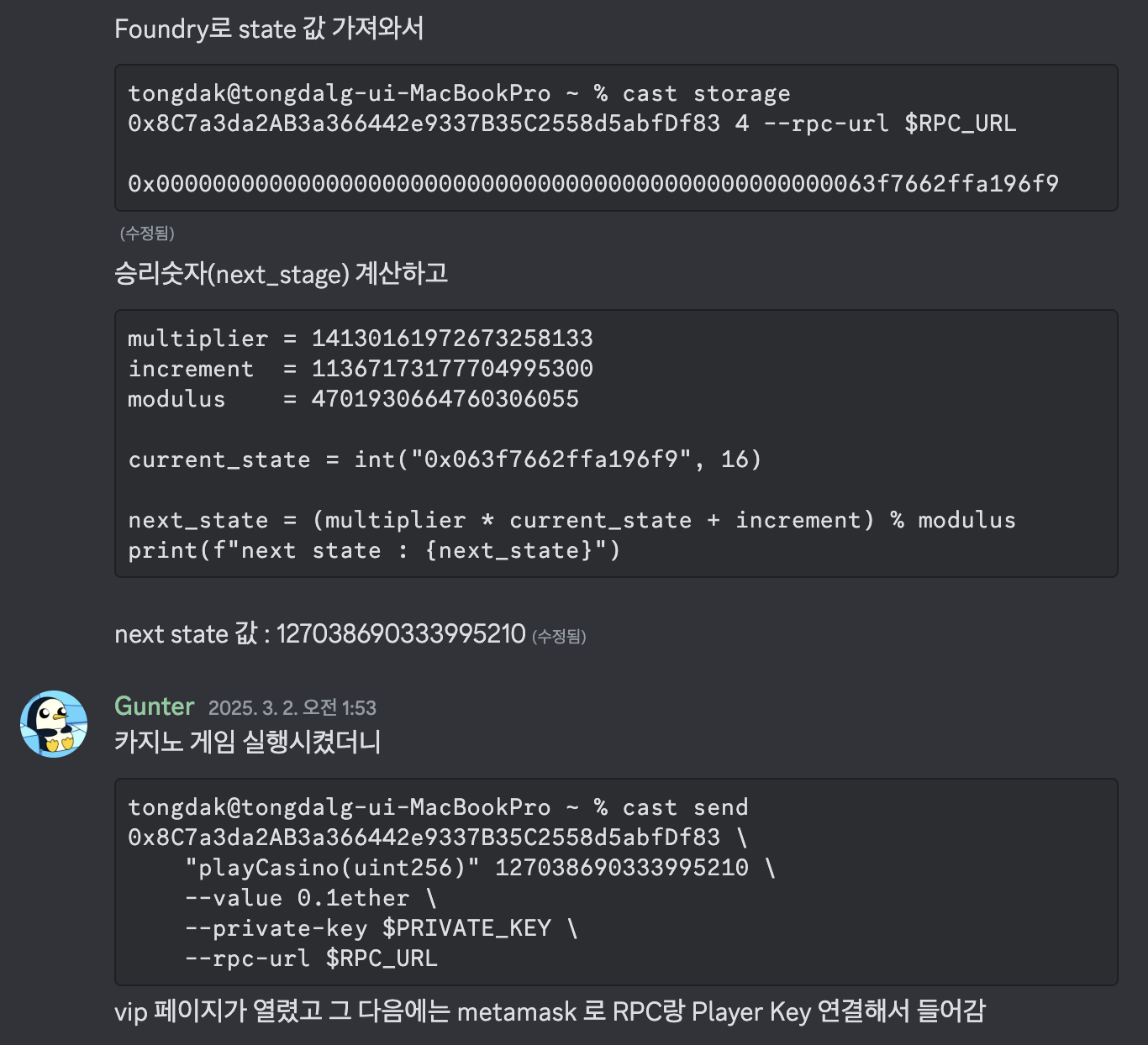
블록체인 재미쪙
