Dreamhack_Textbook-DH_Write up

Description

Alice와 Bob의 통신을 중간자 드림이가 엿보고 있습니다. 둘의 키교환 과정을 공격해 플래그를 획득해주세요 !

플래그 형식은 DH{…} 입니다

.
.

문제 코드

#!/usr/bin/python3
from Crypto.Util.number import getPrime
from Crypto.Util.Padding import pad, unpad
from Crypto.Cipher import AES
import hashlib
import random

class Person(object):
    def __init__(self, p):
        self.p = p
        self.g = 2
        self.x = random.randint(2, self.p - 1)
    
    def calc_key(self):
        self.k = pow(self.g, self.x, self.p)
        return self.k

    def set_shared_key(self, k):
        self.sk = pow(k, self.x, self.p)
        aes_key = hashlib.md5(str(self.sk).encode()).digest()
        self.cipher = AES.new(aes_key, AES.MODE_ECB)

    def encrypt(self, pt):
        return self.cipher.encrypt(pad(pt, 16)).hex()

    def decrypt(self, ct):
        return unpad(self.cipher.decrypt(bytes.fromhex(ct)), 16)

flag = open("flag", "r").read().encode()
prime = getPrime(1024)
print(f"Prime: {hex(prime)}")
alice = Person(prime)
bob = Person(prime)

alice_k = alice.calc_key()
print(f"Alice sends her key to Bob. Key: {hex(alice_k)}")
print("Let's inturrupt !")
alice_k = int(input(">> "))
if alice_k == alice.g:
    exit("Malicious key !!")
bob.set_shared_key(alice_k)

bob_k = bob.calc_key()
print(f"Bob sends his key to Alice. Key: {hex(bob_k)}")
print("Let's inturrupt !")
bob_k = int(input(">> "))
if bob_k == bob.g:
    exit("Malicious key !!")
alice.set_shared_key(bob_k)

print("They are sharing the part of flag")
print(f"Alice: {alice.encrypt(flag[:len(flag) // 2])}")
print(f"Bob: {bob.encrypt(flag[len(flag) // 2:])}")

.
.
.

코드 설명

• 공통으로 사용할 소수 p를 뽑고 각자 알아서 x 준비. 이때 x는 random하게 생성
• 이어서 calc_key()를 실행해 서로에게 공유할 키를 만듦. 이때 공유키 self.k는 (2^x)mod p(pow(self.g, self.x, self.p))로 만듦.
• alice와 bob이 각자 공개키를 만들어서 상대방한테 보냄.
• 이때 중간에 키를 가로채서 상대방에게 키를 속일 수 있음.
• 조작된 상대방의 키 값이 전달되면 상대방은 조작된 키를 가지고 공유키(shared_key)로 설정되게 됨
• 조작된 키를 받은 상대방은 이를 기반으로 AES키를 준비한다.(aes_key)
• 사전에 읽어들인 flag를 반반씩 나눠 이전에 설명한 설정과 함께 AES로 암호화하여 보여줌
  .
  .
  .
  .
  .

Write up

Diffie-Hellman의 가장 큰 약점은 통신하고자하는 상대에 대한 검증이 없는 것이다.

그래서 누구나에게 공개된 a,p 을 통해 제 3자도 동일한 개인키,공개키 쌍을 만들 수 있으며, 중간자와 유효한 키를 분배하게 된다. A->B 로 가는 통신을 가로채 A <-> (나) <-> B 이렇게 통신할 수 있다는 것이다. 그럼 A와 B는 서로 통신하고 있다고 믿게 되지만 중간자에 의해 변조되거나 모두 도청 당할 수 있다.

그래서 A <-> ‘나’ 에 대한 키와 ‘나’ <-> B 에 대한 키가 같다면 같은 키로 암호화 했기 때문에 복호화 역시 같은 키로 할 수 있다.

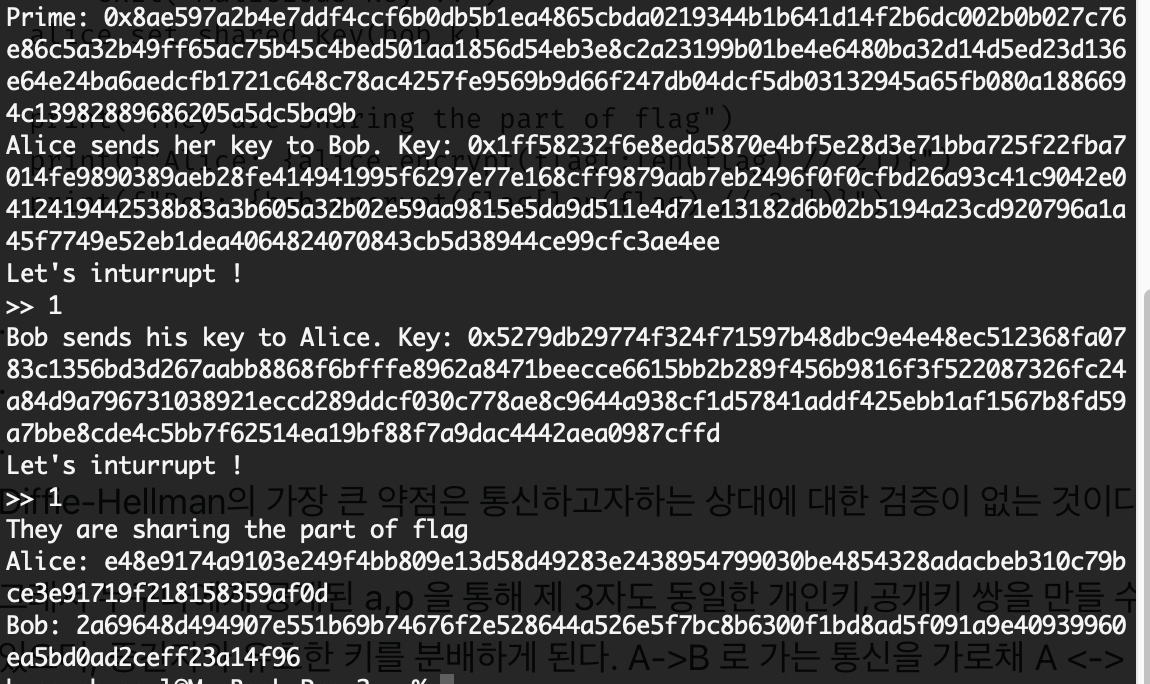
같은 키인 1로 키 교환이 이루어졌을 때 동일한 키로 암호화 했기 때문에 복호화도 정상적으로 이루어졌다.

.
.
.
.

Payload

from Crypto.Cipher import AES
import hashlib
from Crypto.Util.Padding import unpad

prime = b"dd7ec16da4376b1f0ef97e69b2f7f544d8d62c53ca3291058c1ad9dcf7ce0b53fd89bd034337095c78d6dd133721ccaae56b542a06cbdc61407d3f76f00d38d94c72611da709a0df3929b41d850b05f63c46e793ddb3afc38d71e59024346c4dfd07a76e728163b91ff6d15ef6edf924fcb9878b8ac94ffaea6f01df296dd48b"
AESKEY = hashlib.md5(str("1").encode()).digest()

cipher = AES.new(AESKEY, AES.MODE_ECB)

aliceEncryptedData = b"e48e9174a9103e249f4bb809e13d58d49283e2438954799030be4854328adacbeb310c79bce3e91719f218158359af0d"
bobEncryptedData = b"2a69648d494907e551b69b74676f2e528644a526e5f7bc8b6300f1bd8ad5f091a9e40939960ea5bd0ad2ceff23a14f96"

FLAG = unpad(cipher.decrypt(bytes.fromhex(aliceEncryptedData.decode())), 16)
FLAG += unpad(cipher.decrypt(bytes.fromhex(bobEncryptedData.decode())), 16)

print(f"FLAG : {FLAG}")

.
값을 받아서 직접 계산하는 방법.
prime, alice 암호화 데이터, bob 암호화 데이터를 키를 1로 intercept하여 보낸 뒤 각각 모아 위처럼 정리했다.
.
.
.

DH{6625fe941be9a9ad76f0ca7b3250d83d2f8f33ccee8aa5a55a605a3a8e9b7104}