트리

비선형 구조의 여러 구조 중 단방향의 한 구조, 그래프인데 단방향인 거임, 하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮아 있음

특징

• 비선형 구조
  • 데이터를 순차적으로 나열시킨 선형 구조가 아니라, 하나의 데이터 아래에 여러 개의 데이터가 존재할 수 있는 비선형 구조
• 사이클이 없음
  • 사이클: 시작 노드에서 출발해 다른 노드를 거쳐 시작하는 것
  • 트리는 사이클(cycle)이 없는 하나의 연결 그래프 (Connected Graph)
• 용어
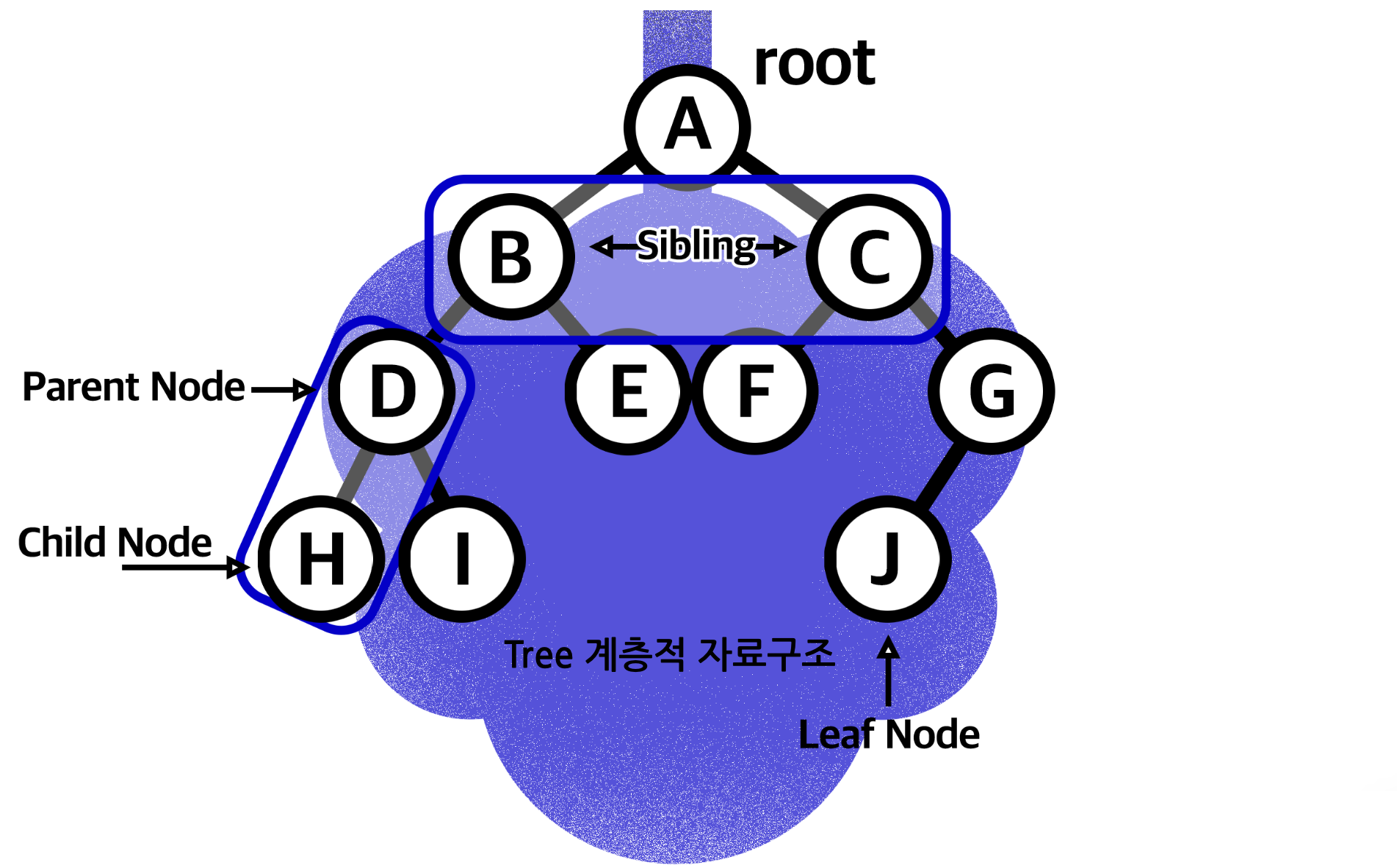
  • 노드: 트리 구조를 이루는 모든 개별 데이터
  • 트리는 '루트' 노드부터 시작해 그 자식인 '자식' 노드, 자식이 또 부모가 되는 '부모'노드, 자식끼리는 '형제' 노드, 제일 막내 노드는 '리프' 노드
• 측정데이터:
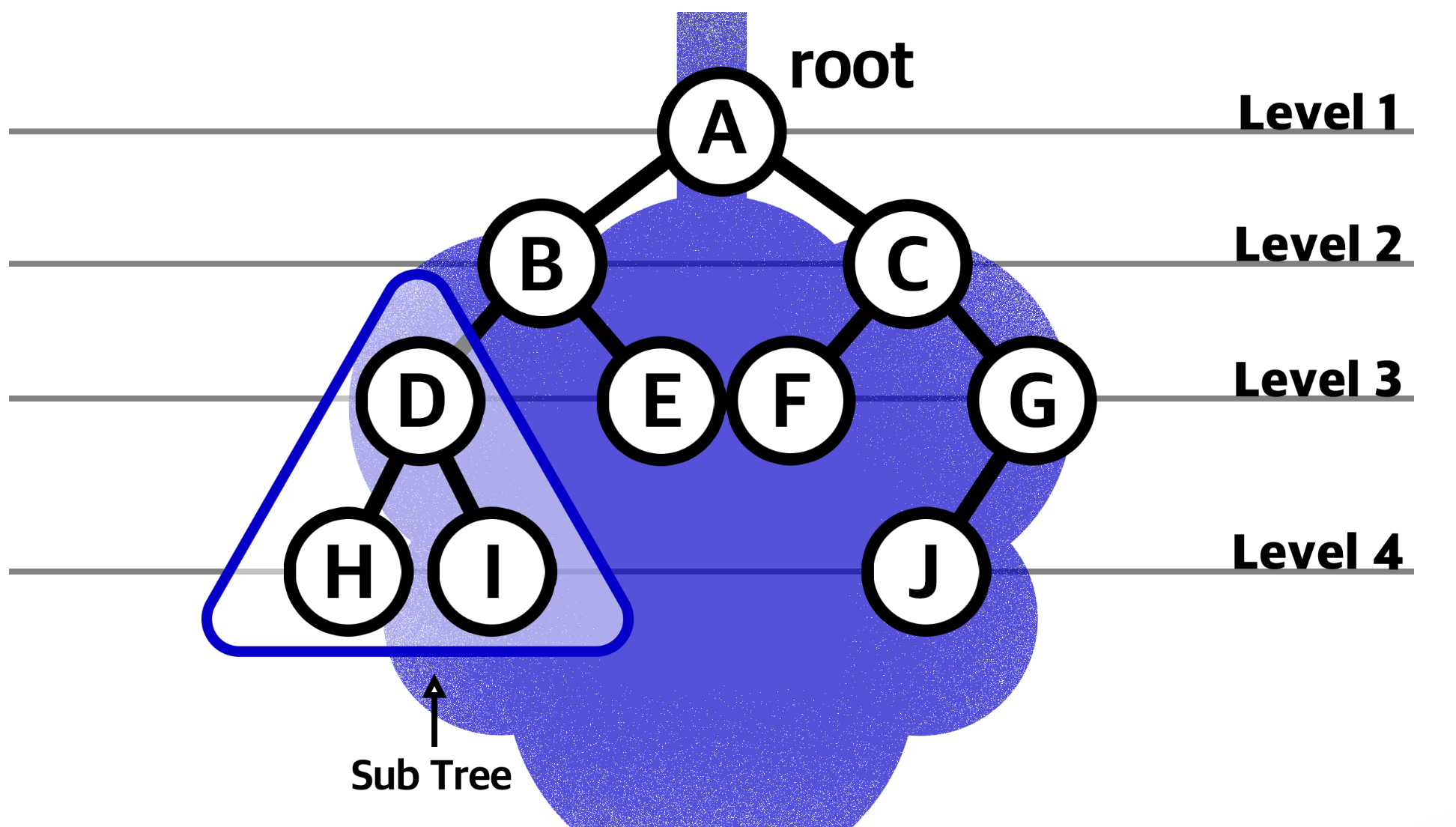
  • 깊이(Depth): 루트 노드 0부터 시작해서 자식 노드로 하나씩 내려갈 때마다 깊이가 1씩 증가
  • 레벨(Level): 같은 깊이들을 묶어 레벨로 표현
  • 높이(Height): 리프 노드 0부터 시작해 부모 노드로 하나씩 올라갈 때마다 높이가 1씩 증가
  • 서브 트리: 트리 구조를 갖춘 작은 트리를 서브 트리

예시

• 컴퓨터의 디렉토리 구조: 모든 폴더는 하나의 폴더(루트 폴더, /)에서 시작되어, 가지를 뻗어나가는 모양새
  
• 가계도
• 회사 직책
• 월드컵 토너먼트 대진표

이진 트리

효율적인 탐색을 위해 고민하여 나온 것이 이진 트리다!

자식 노드가 최대 두 개인 노드들로 구성된 트리, 두 개의 자식 노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 나눔

특징

자료의 삽입, 삭제 방법에 따라 정 이진 트리(Full binary tree), 완전 이진 트리(Complete binary tree), 포화 이진 트리(Perfect binary tree)로 나눈다!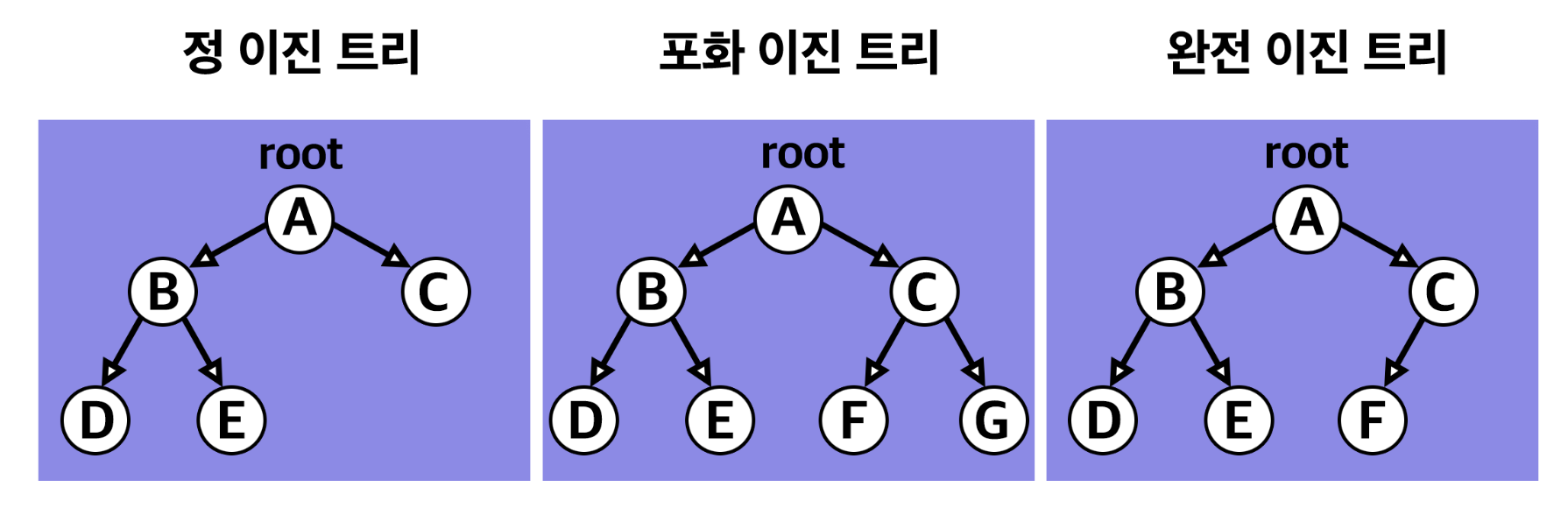

• 정 이진 트리 : 각 노드가 0개 혹은 2개의 자식 노드를 가짐.
• 포화 이진 트리 : 정 이진 트리이면서 완전 이진 트리인 경우. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리.
• 완전 이진 트리 : 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져야 함.

이진 탐색 트리

Binary Search Tree, 이진 탐색(binary search)과 연결 리스트(linked list)를 결합한 이진트리

• 각 노드에 중복되지 않는 키(Key)가 있음.
• 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있음.
• 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있음.
• 좌우 서브트리도 모두 이진 탐색 트리여야 함.
  단점: 균형 잡힌 트리가 아닐 때, 입력되는 값의 순서에 따라 한쪽으로 노드들이 몰리게 될 수 있음, 해결하고 싶다면 삽입과 삭제마다 트리의 구조를 재조정하는 과정을 거치는 알고리즘을 추가해야한다!

즉, 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징을 가진다!

특징

• 효율성: 기존 이진 트리보다 탐색이 빠르다는 장점
  • 트리의 높이가 h(height)라면 o(h)의 복잡도
• 탐색 과정: 원하는 값이 나올 때까지 반복해 진행!
  • 루트 노드의 키와 찾고자 하는 값을 비교. 만약 찾고자 하는 값이라면 탐색을 종료.
  • 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행.
  • 찾고자 하는 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리로 탐색을 진행.

예시

5라는 값을 찾고자 한다.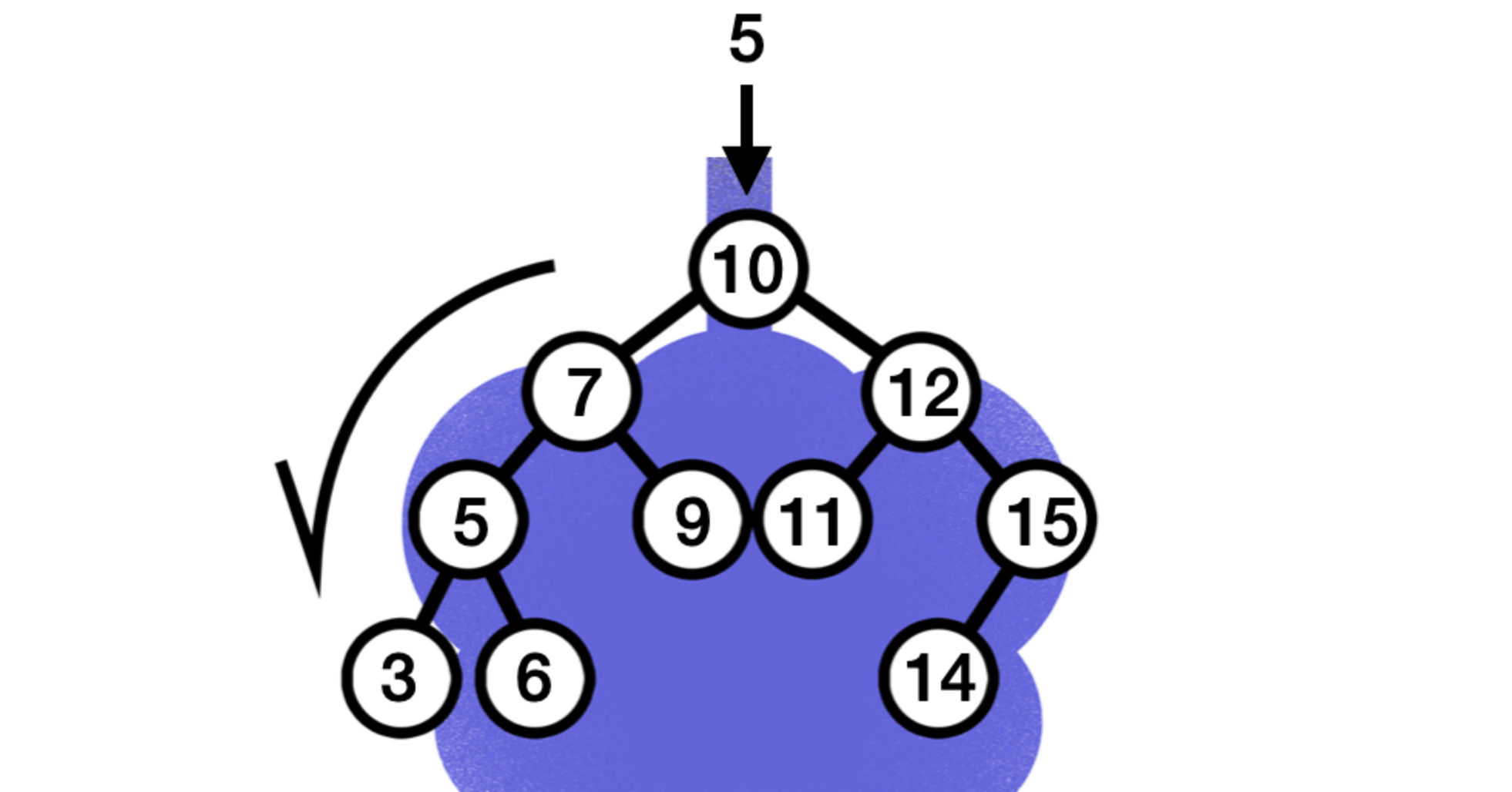

1. 제일 처음에는 루트 노드와 값을 비교
2. 루트 노드가 여기서는 10이므로 루트노드보다 작기 때문에, 왼쪽 서브 트리로 탐색 시작
3. 마주친 노드는 7이고, 찾고자 하는 값은 5이므로 다시 7을 기준으로 왼쪽 서브 트리로 탐색 진행
4. 만난 값이 찾고자 하는 값이므로 탐색이 종료

만약 3을 찾는다면 4번의 연산이 진행되었을 것. 즉! 트리 안의 값을 찾는다면 무조건 트리의 높이(h) 이하의 탐색

핵심: 트리 안에 찾고자 하는 값이 없더라도 최대 h번의 연산 및 탐색이 진행

1. 만일 13이라는 숫자를 찾는다고 가정. 마지막으로 도착하는 노드의 값은 14인데, 여기서 13은 14보다 작으므로 왼쪽 서브 트리로 탐색을 진행
2. 오른쪽 서브 트리가 없으므로 14에서 탐색이 종료

즉! 최대 h번의 연산 및 탐색이 진행 - 트리의 높이(h) 이하의 탐색, 시간복잡도는 O(h)!

트리 순회

특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것, 모든 노드를 방문하기 위해서 일정한 조건이 필요, 트리 구조를 유지보수하거나 특정 목적을 위해서도 순회 방법에 대한 정의는 필수적으로 필요

트리 순회는 크게 DFS(Depth-First Search)와 BFS(Breadth-First Search)로 나눌 수 있다.

지그재그 순회, 모리스 순회, 경계 순회, 대각선 순회 등이 있지만 가장 유명한 순회만 살펴보겠다.

DFS (깊이 우선 탐색)

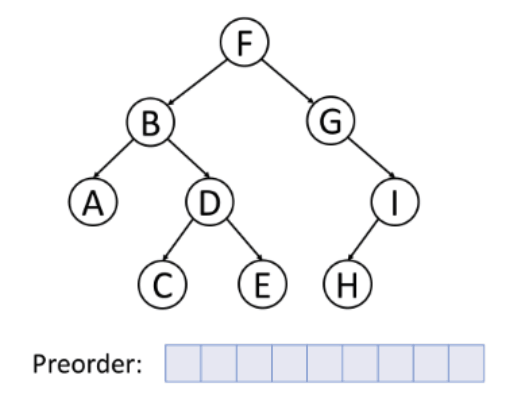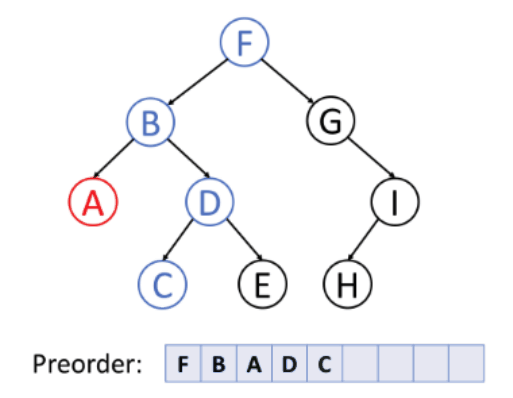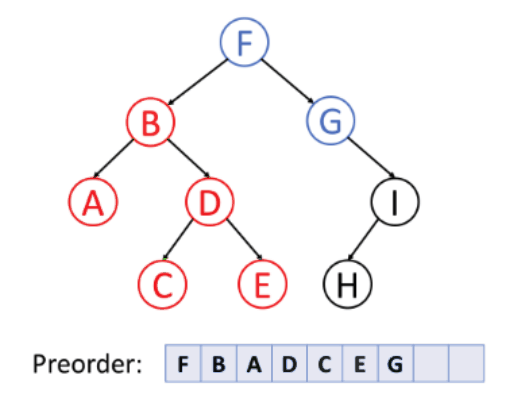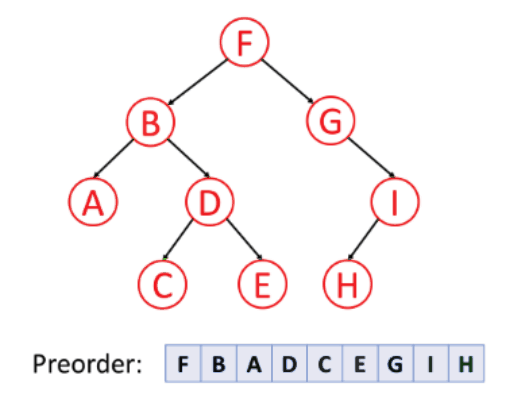
1. 전위 순회 (preorder traverse)

• 순서: 루트 → 왼쪽 → 오른쪽
• 특징: 주로 부모 노드가 먼저 생성되어야 하는 트리를 복사할 때 적합!

2. 중위 순회 (inorder traverse)

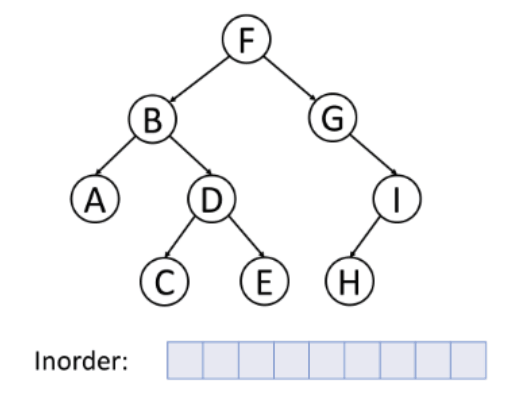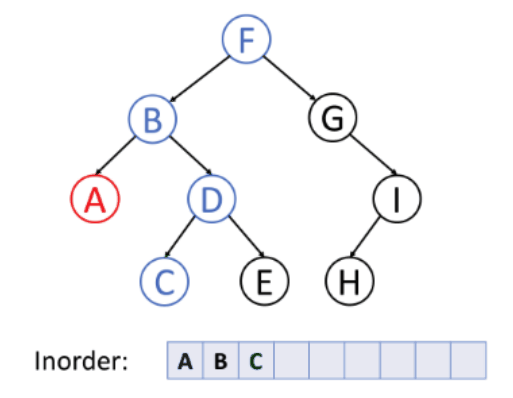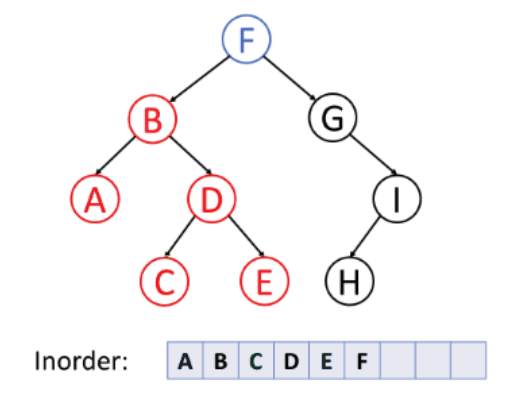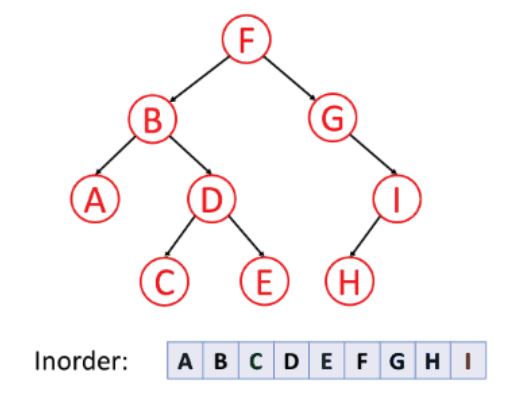
• 순서: 왼쪽 → 루트 → 오른쪽, 루트를 중간에 순회, 부모 노드가 서브 트리의 방문 중간에 방문되는 순회 방식
• 특징: 이진 탐색 트리의 오름차순으로 값을 가져올 때 적합!

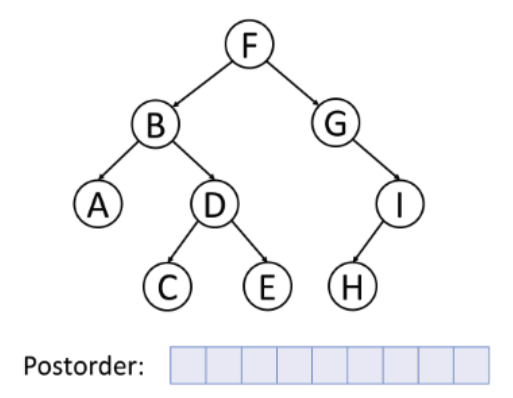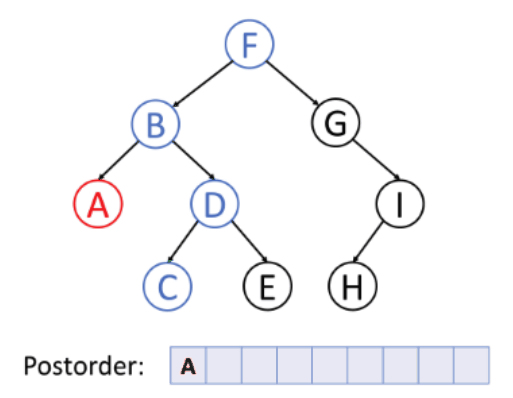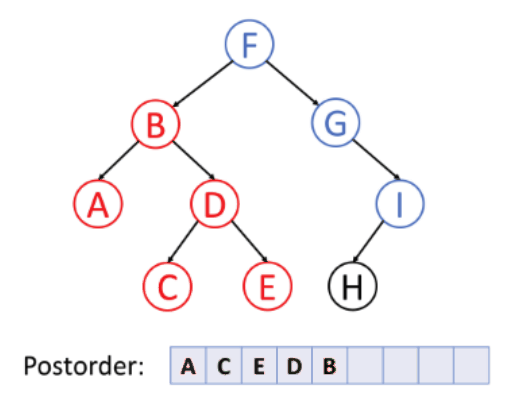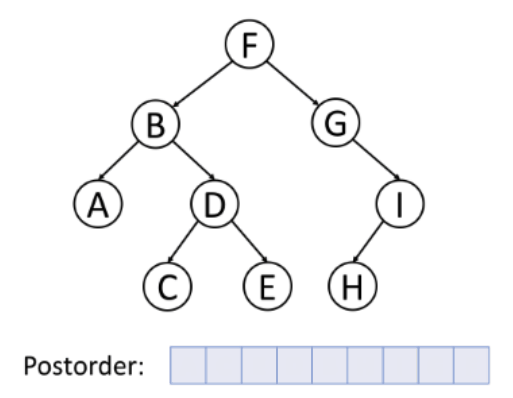
3. 후위 순회 (postorder traverse)

• 순서: 왼쪽 → 오른쪽 → 루트, 루트를 가장 마지막에 순회
• 특징: 자식 노드부터 삭제해야 하는 트리 삭제에 적합, 자식 노드가 먼저 삭제되어야 상위 노드를 삭제할 수 있기 때문

BFS (너비 우선 탐색)

레벨 순회(Level-order Traverse)라고도 하며, 같은 레벨의 노드들을 왼쪽에서 오른쪽으로 순회한다.

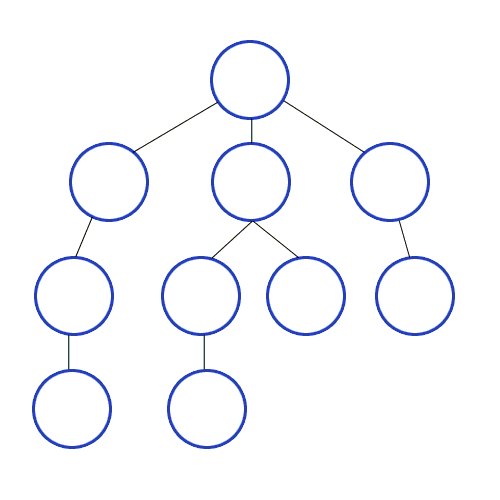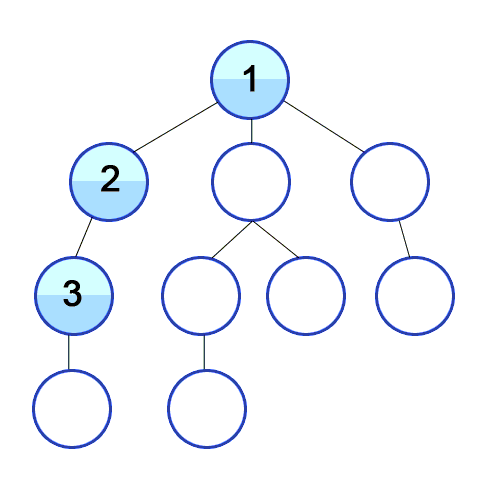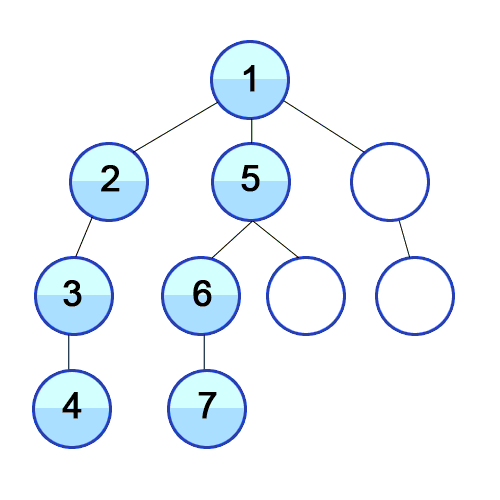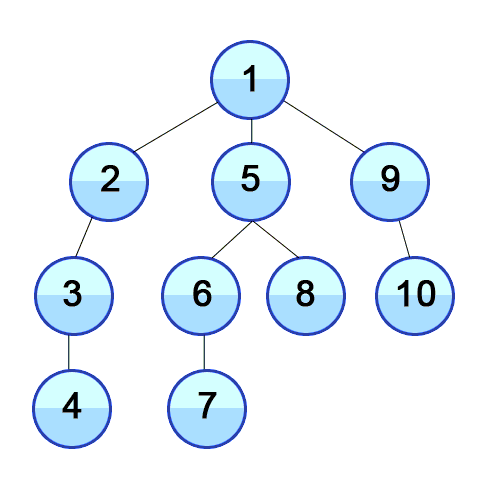
아래와 같은 방법을 요구할 때, 적합하다!

1. 최단 경로 찾기

   • 시작점에서 목표까지의 최단 거리나 최소 단계를 찾을 때
   • 모든 간선의 가중치가 동일한 경우에 최적
   • 예: 미로에서 출구까지의 최단 경로, 소셜 네트워크에서의 최소 연결 단계

2. 레벨 단위 처리가 필요한 경우

   • 트리의 각 레벨별로 데이터를 처리해야 할 때
   • 예: UI 렌더링의 계층 구조, 조직도 시각화

3. 그래프의 연결 요소 탐색

   • 특정 노드와 가까운 모든 노드를 찾을 때
   • 네트워크상의 가까운 이웃 노드 탐색
   • 예: 소셜 네트워크의 친구 추천 시스템

4. 상태 공간 탐색

   • 모든 가능한 상태를 체계적으로 탐색할 때
   • 게임의 다음 수 탐색
   • 예: 루빅큐브 최소 움직임 찾기, 퍼즐 게임 솔버

5. 동심원적 탐색이 필요한 경우

   • 중심점에서부터 거리에 따라 점차적으로 확장하며 탐색해야 할 때
   • 예: 전염병 확산 시뮬레이션, 물결 효과 구현

구현

// 최단 경로 찾기 예시
function findShortestPath(graph, start, end) {
    const queue = [[start, [start]]];
    const visited = new Set([start]);
    
    while (queue.length > 0) {
        const [current, path] = queue.shift();
        
        if (current === end) {
            return path;
        }
        
        for (let neighbor of graph[current]) {
            if (!visited.has(neighbor)) {
                visited.add(neighbor);
                queue.push([neighbor, [...path, neighbor]]);
            }
        }
    }
    
    return null; // 경로가 없는 경우
}

요약: 트리 순회의 DFS vs BFS 비교

특성	BFS (너비 우선 탐색)	DFS (깊이 우선 탐색)
탐색 방식	레벨 단위로 너비 우선 탐색	한 경로를 끝까지 탐색 후 백트래킹
자료구조	큐(Queue) 사용	스택(Stack) 또는 재귀 사용
메모리	큐에 동일 레벨의 모든 노드 저장으로 많은 메모리 필요	현재 경로의 노드만 저장하여 적은 메모리 사용
최적화	최단 경로 보장 (가중치가 없거나 동일한 경우)	최단 경로 보장하지 않음
완전성	유한 그래프에서 해 존재시 반드시 찾음	무한 그래프에서도 해를 찾을 수 있음
적합한 경우	• 최단 경로 찾기 • 레벨 단위 처리 • 인접 노드 탐색 • 상태 트리가 넓지만 얕은 경우	• 경로 존재 여부 확인 • 사이클 탐지 • 위상 정렬 • 상태 트리가 깊고 좁은 경우
시간 복잡도	O(V + E) - V는 정점, E는 간선	O(V + E) - V는 정점, E는 간선
구현 복잡도	상대적으로 단순	재귀로 인해 상대적으로 복잡
방문 순서	시작점에서 가까운 순서대로 방문	한 방향으로 최대한 깊이 방문
백트래킹	불필요	필요 (이전 분기점으로 돌아가야 함)

1. BFS 사용이 좋은 경우

   • 네트워크에서 가장 가까운 서버 찾기
   • 소셜 네트워크에서 친구 추천
   • 미로에서 출구까지의 최단 거리
   • GPS 내비게이션 최단 경로

2. DFS 사용이 좋은 경우

   • 미로에서 경로 존재 여부 확인
   • 게임의 퍼즐 솔버
   • 그래프의 연결 요소 찾기
   • 위상 정렬이 필요한 작업 스케줄링