[알고리즘 문제 해결 전략] 06.3 문제: 소풍 (문제 ID: PICNIC)

Daniel Oh·2023년 11월 4일

algorithm algospot ps

알고리즘 문제 해결 전략

목록 보기

3/7

1 문제

링크

알고리즘 문제 해결 전략의 첫번째 문제... 첫 문제이므로 빡세게 공부해야지!

2 문제 해결 알고리즘

독해: 문제를 읽고 이해한다.

재정의+추상화: 문제를 익숙한 용어로 재정의한다.

설계: 어떻게 해결할지 계획을 세운다.

검증: 계획을 검증한다.

구현: 프로그램을 구현한다.

회고: 어떻게 풀었는지 돌아보고, 개선할 방법이 있는지 찾아본다.

2-1 독해

친구의 명 수와, 누구끼리 친구인지에 대한 정보가 주어질 때, 모든 학생을 짝 지어줄 수 있는 경우의 수 구하기 문제이다.

"누구끼리 친구인지에 대한 정보": (a, b)와 (b, a)는 동일한 정보이다.

"경우의 수 구하기": 무식하게 풀기의 근간으로, 완전 탐색 (재귀 호출)이 떠오르는 대목이다.

2-2 재정의

예제를 대입해보며 읽다보면, 결국 친구 쌍 중 어느 친구라도 중복되지 않도록 고르는 경우의 수를 구하는 것이라는 것을 알 수 있다. 즉, [(a, b), (c, d)]를 골랐다면, a, b, c, d를 모두 포함하지 않은 (예를 들어 (e, f)) 순서쌍만을 고를 수 있다는 뜻이다. ((a, e)는 고를 수 없다.)

(물론 친구 쌍에 모든 친구가 포함되지 않을 수도 있지 않느냐 할 수 있지만... 예제를 보니 그런 경우는 없는 것 같고, 또 출력에 모든 학생을 친구끼리만 짝지어줄 수 있는 방법의 수라고 적혀있기 때문에, 모든 학생이 최소한 친구 하나씩은 가지고 있는 것 같다. ~~왕따는 없는듯~~)

2-3 설계

2-3-a 직관

떠오르지 않는다... 입력부터 막막한 걸... 일단 어찌저찌 입력을 받았다고 하더라도... 뒤가 안 풀리네...

2-3-b 체계적인 접근

2-3-b-1 비슷한 문제를 풀어본 적이 있나?

있다! 바로 책 149p의 n개의 원소 중 m개를 고르는 모든 조합을 찾는 알고리즘이다. (자세한 내용)

// n : 전체 원소의 수
// picked : 지금까지 고른 원소들의 번호
// toPick : 더 골라야할 원소의 수

void pick(int n, vector<int>& picked, int toPick){
	// 더 고를 원소가 없는 경우 원소들을 출력
	if(toPick == 0){
		printPicked(picked);
		return;
	}
    
	// 고를 수 있는 가장 작은 번호 계산
	int smallest = picked.empty() ? 0 : picked.back() + 1;
    
	// 원소를 하나 골라서 재귀함수 호출
	for(int next = smallest; next < n; ++next){
		picked.push_back(next);
		pick(n, picked, toPick-1)
		picked.pop_back();
	}
}

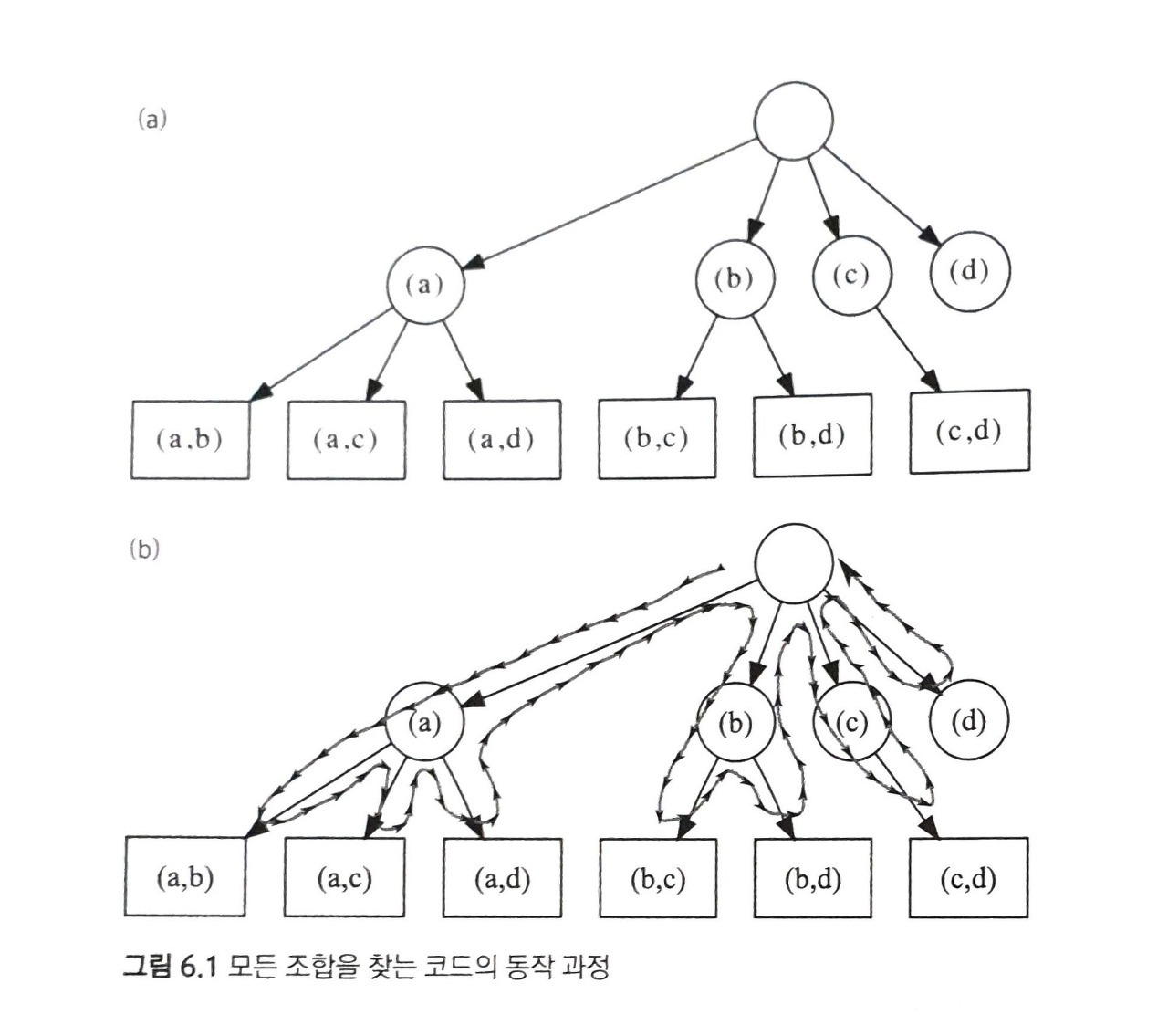
즉, 요런 느낌이다. 우리의 목표도 친구 쌍 중 어느 친구라도 중복되지 않도록 고르는 경우의 수를 구하는 것이므로,

친구 쌍 하나를 고르고
재귀함수를 호출하고
고른 친구 쌍을 빼고
1~4를 모든 친구 쌍에 걸쳐 반복

하면 되지 않을까?

2-3-b-5 그림으로 그려볼 수 있나?

해당 생각은 문제를 풀고나서 들긴 했지만.. 음.. 그래도 적어보겠다.

예제 입력

4 6
0 1 1 2 2 3 3 0 0 2 1 3

은 다음과 같이 해석된다.

'0, 1, 2, 3 중 6개의 친구 쌍 [(0,1), (1,2), (2,3), (3,0), (0,2), (1,3)]

이를 2차원 좌표 평면에 올려보면??

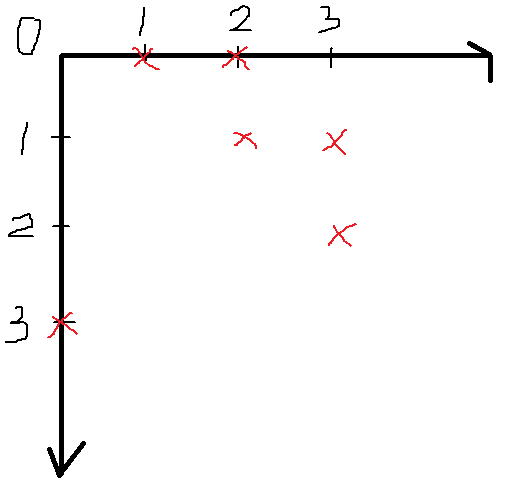
친구 쌍 중 어느 친구라도 중복되지 않도록 고르는 경우의 수는 한 점을 취하기로 정하면 해당 점의 가로선, 세로선는 고를 수 없다는 것을 의미한다. 예를 들어 (a,b)를 고르면 (a,?), (b,?), (?,a), (?,b)는 고를 수 없다.

따라서 (0,1)을 고르면 (2,3)만을 고를 수 있고,

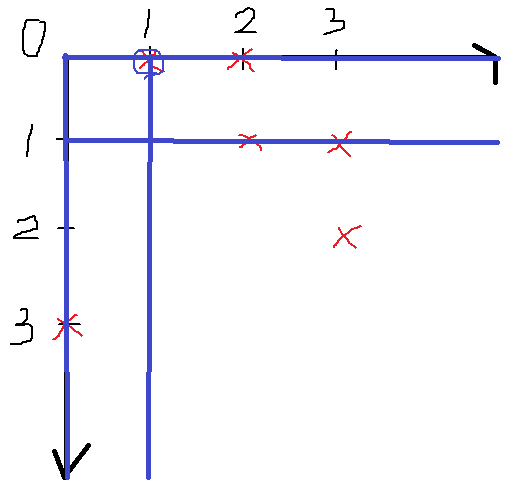
(0,2)을 고르면 (1,3)만을 고를 수 있고,

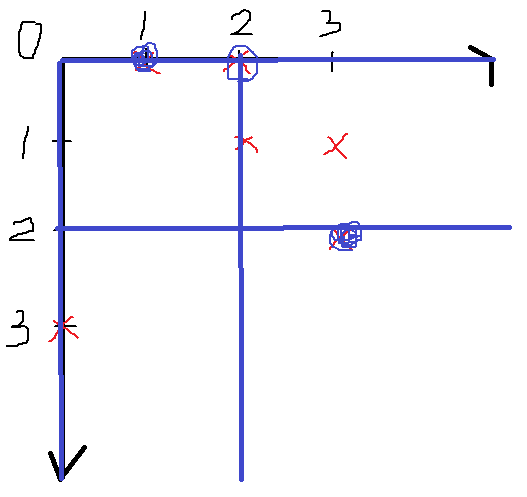
(1,2)을 고르면 (3,0)만을 고를 수 있다.

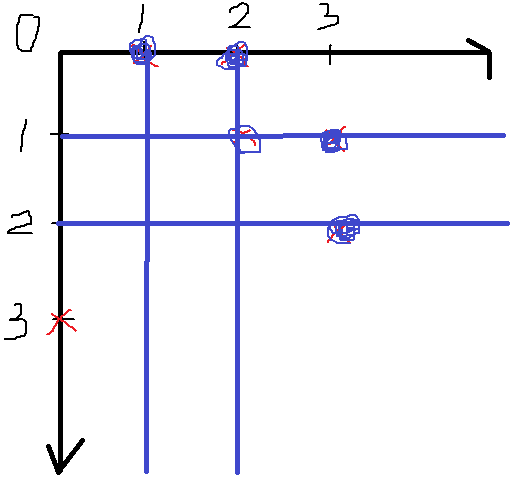
따라서 가짓수는 3개이다.

즉, 친구 쌍들을 좌표평면 위에 표시하고 조건에 따라 다음 선택의 제한을 주며 0부터 n-1까지 다 채우는 경우의 수를 세면 된다.

2-4 검증

2-4-1 재귀로 완전 탐색하는 방법

basecase를 몇 번 찍을지를 생각해보면 된다. 최악의 경우는 m=nC2로 모두가 서로의 친구라고 주는 경우이다. 이 경우 basecase가 nC2번 찍히므로 nC2=n*(n-1)/2이다. 따라서 시간 복잡도는 O(n^2)이다.

n의 최댓값은 10이므로 최악의 경우 100번 연산을 해야하고, 이는 주어진 시간 1초 (1000ms) 내에 충분히 해결될 수 있다.

2-4-2 좌표평면 위에서 지우는 방법

역시 최악의 경우는 모두가 서로의 친구라고 주는 경우이다.

이 경우 점 하나를 취하고 지운 나머지 점의 개수는 항상 1부터 n-3까지의 합개이다. 즉, (n-3)(n-2)/2이다. (귀납적으로 유도했다.)

따라서 시간복잡도는... 잘 모르겠음. ㅠ 좀 더 생각해 보아야겠다.

2-5 구현

2-4-1 재귀로 완전 탐색하는 방법

의사 코드를 작성해보자.

void pick(뽑은친구쌍벡터, 더고를친구쌍수)
	if (더고를친구쌍수 = 0) cnt++; return;
    int startIndex = find(친구쌍벡터, 뽑은친구쌍벡터.back())
    for (int i = startIndex; i < 친구쌍수; ++i) 
    	if (친구쌍벡터[i]의 원소 둘 다 뽑은친구쌍벡터내에 없다면)
        	뽑은친구쌍벡터.push_back(친구쌍벡터[i]);
            pick(뽑은친구쌍벡터, 더고를친구쌍수 - 1);
            뽑은친구쌍벡터.pop_back();

구현한 코드는 다음과 같다.

#include <bits/stdc++.h>
// #include "bits/stdc++.h"
#define endl "\n"
#define all(x) (x).begin(), (x).end()
#define sz(x) (uint)(x).size()
using namespace std;
using lld = long long;
using pii = pair<int, int>;
using pll = pair<lld, lld>;

uint cnt;
vector<pii> friendPair;

int findIndexOfPairInListOfPair(pii pair, vector<pii>& pairs) {
    for (uint i = 0; i < sz(pairs); ++i) {
        if (pair.first == pairs[i].first && pair.second == pairs[i].second) return i;
    }
    return -1;
}

int tailIndexPlusOneIncludingEmpty(vector<pii>& v) {
    if (sz(v) == 0) return 0;
    pii tail = v.back();
    return findIndexOfPairInListOfPair(tail, friendPair) + 1;
}

bool isElementInPairNotExistInListOfPair(pii pair, vector<pii>& pairs) {
    for (uint i = 0; i < sz(pairs); ++i) {
        if (pair.first == pairs[i].first || pair.first == pairs[i].second
            || pair.second == pairs[i].first || pair.second == pairs[i].second) return false;
    }
    return true;
}

void pickAndUpdateCnt(vector<pii>& pickedFriendPair, int numOfRestFriendPair) {
    // cout << "numOfRestFriendPair " << numOfRestFriendPair << endl;
    if (numOfRestFriendPair == 0) { cnt++;
    // cout << "cnt " << cnt << endl;
    return; }

    int startIndex = tailIndexPlusOneIncludingEmpty(pickedFriendPair);
    // cout << "startIndex " << startIndex << endl;
    
    for (int i = startIndex; i < sz(friendPair); ++i) {
        // cout << "{" << "i " << i << " among " << sz(friendPair) << endl;
        if (isElementInPairNotExistInListOfPair(friendPair[i], pickedFriendPair)) {
            pickedFriendPair.push_back(friendPair[i]);
            pickAndUpdateCnt(pickedFriendPair, numOfRestFriendPair - 1);
            pickedFriendPair.pop_back();
        }
        // cout << "i " << i << " among " << sz(friendPair) << "}" << endl;
    }

    return;
}

int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
        
    uint c;
    cin >> c;
    // cout << c << endl;

    for (uint i = 0; i < c; ++i) {
        uint n, m;
        cin >> n >> m;
        // cout << n << " " << m << endl;
        friendPair.resize(m);
        for (uint j = 0; j < m; ++j) {
            int a, b;
            cin >> a >> b;
            // cout << a << " " << b << endl;
            friendPair[j] = make_pair(a, b);
        }

        vector<pii> pickedFriendPair;
        cnt = 0;
        pickAndUpdateCnt(pickedFriendPair, n / 2);
        cout << cnt << endl;
    }

    return 0;
}

의사 코드 작성하고 한 3시간 동안 끙끙댔던 것 같다.

좋은 코드를 작성하기 위한 원칙 적용

간결한 코드 작성: 답을 내기 위한 cnt와 friendPair에서 글로벌 변수를 사용했다.
적극적으로 코드 재사용: 평소 함수를 많이 만들어봤자 1~2개였건만... 이번에는 최대한 작은 단위로 쪼개 함수를 무려 3개나 만들었다.
표준 라이브러리 공부: std::vector와 std::pair에 대한 내용을 헷갈려 약간 헤멨다. 그래도 표준 라이브러리 사이트가 잘 되어 있어서 쉽게 해결했다.
항상 같은 형태로 프로그램 작성: n개의 원소 중 m개를 고르는 모든 조합을 찾는 알고리즘 과 유사한 형태의 코드로 작성되었다. (단, 원소를 고르는 조건이 추가되었을 뿐!)
명료한 명명법 사용: 함수 이름, 변수 이름에 특히 공들였다. 옛날 같았으면 극혐했을 변수 이름이지만, 지금 보니 술술 읽혀 좋다. (isElementInPairNotExistInListOfPair은 좀 뇌절인 것 같기도..?)
모든 자료를 정규화하여 사용: 아.. 이건 사실 잘 못 지킨 것 같다. 앞서 "누구끼리 친구인지에 대한 정보": (a, b)와 (b, a)는 동일한 정보이다. 이 정보는 더 멋지게 처리할 수도 있었을 것 같다. 하지만 그냥 isElementInPairNotExistInListOfPair 이 함수에서 다음과 같이 처리했다.

if (pair.first == pairs[i].first || pair.first == pairs[i].second
            || pair.second == pairs[i].first || pair.second == pairs[i].second) return false;
    }

채점 결과

결과는 한 번에 (마이너한 오류 제외)

정답~!

2-6 회고

2-6-1 입력

입력 부분에서 막히면 안된다. 이번 문제의 입력은 좀 괴랄하긴하다.

cin은 \n(줄바꿈) 또는 (공백)으로 쪼개어 입력된다.

테스트 케이스 (`c`) 주어지는 경우

반복문을 c번 돌리면 된다.

int main()
{
    uint c;
    cin >> c;

    for (uint i = 0; i < c; ++i) {
        테스트 케이스에 대한 입력
        입력 처리
        테스트 케이스에 대한 출력
    }

    return 0;
}

숫자 여러 개 입력받는 경우

숫자 개수에 맞게 cin >> .. >> ..을 작성하면 된다.

int main()
{
    uint a, b;
    cin >> a >> b >> c >> ... ;

    return 0;
}

벡터에 숫자 저장

보통 몇 개의 숫자를 받을지 준다. (n) 미리 벡터를 만들고, 벡터의 사이즈를 조정한다. (push_back은 잘 안쓰는 것 같다. 입력 받을 때에는 indexing을 해서 넣어주자.)

int main()
{
    uint n;
    cin >> n;
    
    vector<number> v(n); 만약 v를 글로벌로 이미 정의했다면 v.resize(n);
    for (uint i = 0; i < n; ++i) {
    	cin >> v[i]
    }

    return 0;
}

숫자를 끊어서 벡터에 저장해야 하는 경우

그럼 해당 문제 같은 입력은 어떻게 처리하지? 이렇게 for문 안에서 끊고자 하는 숫자 단위만큼 cin으로 입력 받아 처리할 수 있다.

int main()
{
    uint n, m;
    cin >> n >> m;
    
    vector<number> v(n); 만약 v를 글로벌로 이미 정의했다면 v.resize(n);
    for (uint i = 0; i < m; ++i) {
    	int a, b;
        cin >> a >> b;
    	v[i] = make_pair(a, b);
    }

    return 0;
}

이번 문제의 입력

int main()
{
    uint c;
    cin >> c;

    for (uint i = 0; i < c; ++i) {
        uint n, m;
        cin >> n >> m;
        friendPair.resize(m);
        for (uint j = 0; j < m; ++j) {
            int a, b;
            cin >> a >> b;
            friendPair[j] = make_pair(a, b);
        }

        입력 처리
        테스트 케이스에 대한 출력
    }

    return 0;
}

2-6-2 전역 변수의 활용

...

uint cnt; 					// cnt 정의
vector<pii> friendPair; 	// friendPair 정의

...

int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
        
    uint c;
    cin >> c;
    // cout << c << endl;

    for (uint i = 0; i < c; ++i) {
        uint n, m;
        cin >> n >> m;
        // cout << n << " " << m << endl;
        friendPair.resize(m);
        for (uint j = 0; j < m; ++j) { 		// 해당 for문을 통해 friendPair가 초기화된다.
            int a, b;
            cin >> a >> b;
            // cout << a << " " << b << endl;
            friendPair[j] = make_pair(a, b);
        }

        vector<pii> pickedFriendPair;
        cnt = 0;	 						// cnt는 여기서 초기화된다.
        pickAndUpdateCnt(pickedFriendPair, n / 2);
        cout << cnt << endl;
    }

    return 0;
}

답을 내기 위한 cnt와 friendPair에서 글로벌 변수를 사용했다. 열심히 만든 함수들에서의 접근을 용의하게 만들기 때문이다. 만약 글로벌로 안 놓았다면 이들을 일일이 인자로 넘겨야 하기 때문에, 꽤나 코드가 복잡해졌을 것이다.

주의 사항은, 이들은 초기화를 잘 시켜주어야 한다는 것이다. 다음 테스트 케이스로 넘어가기 전에 이전 테스트 케이스의 결과값이 cnt에 넘어간다면 곤란하다. (따라서 처음부터 값을 초기화하지 말고, 처음에는 비워놓았다가 사용하기 직전에 값을 수정하자.)

함수에서 값의 접근을 용의하게 만들기 위해 전역 변수를 화활용할 수 있다. 단, 값을 초기화하는데 유념하자!

2-6-3 표준 라이브러리: `vector`, `pair`

벡터의 크기를 바꾸고 싶을 경우 vector.resize(size) 함수를 사용한다. 이는 벡터가 전역 변수로 정의되어 있을 때, 벡터를 정의하며 크기를 명시할 수 없기에 유용한다. (정확히는 크기를 명시해도 크기가 테스트 케이스마다 바뀌기 때문에...)

vector.front()와 vector.begin(), vector.back()과 vector.end()를 헷갈리지 않는다. 전자는 원소를 반환하고, 후자는 Iterator를 반환한다.

// 사용되는 매크로 및 기타 등등
#include <bits/stdc++.h>
// #include "bits/stdc++.h"
#define endl "\n"
#define all(x) (x).begin(), (x).end()
#define sz(x) (uint)(x).size()
using namespace std;
using lld = long long;
using pii = pair<int, int>;
using pll = pair<lld, lld>;

벡터의 크기를 알고 싶을 경우 vector.size() 대신 sz(vector) 매크로를 적극 활용하자. 코드가 간결해진다.

pair를 사용할 때에도 pair<int, int> 대신 pii 매크로를 적극 활용하자. 코드가 간결해진다.

// make_pair를 이용한 pair 생성
for (uint j = 0; j < m; ++j) {
	int a, b;
    cin >> a >> b;
    friendPair[j] = make_pair(a, b);
}

pair를 정의할 때에는 그냥 pair(a,b)가 아니고 make_pair(a,b)이다.

2-6-4 재귀 함수 작성 Tip

재귀 함수는 두 가지 종류로 나뉜다. 집합의 원소 하나하나를 고르거나 말거나 반복하며 결과를 만들어 출력하는, 개수를 세는 재귀 함수와 기저에서 boolean을 반환하여 여러 가능성 중에서 ~ 가능한 경우가 한 가지는 있더라 / 아예 안 되더라라는 재귀 함수가 있다.

이번 경우는 전자이다. 출력하는 or 개수를 세는 재귀 함수이기 때문이다. 해당 함수의 알짜 코드는 다음과 같다.

// n : 전체 원소의 수
// picked : 지금까지 고른 원소들의 번호
// toPick : 더 골라야할 원소의 수

void pick(int n, vector<int>& picked, int toPick){
	// 더 고를 원소가 없는 경우 원소들을 출력 또는 개수 세기
	if(toPick == 0) {
		printPicked(picked); 또는 cnt++;
		return;
	}
    
	// 고를 수 있는 원소들의 집합 순회하며 재귀함수 호출
	for(next = 원소 in 고를 수 있는 원소들의 집합) {
    	if (next가 조건을 충족함) {
            picked.push_back(next);
            pick(n, picked, toPick-1)
            picked.pop_back();
        }
	}
}

집합의 원소 하나하나를 고르거나 말거나 반복하며 결과를 만들어 출력하는, 개수를 세는 재귀 함수는 다음과 같은 과정을 거친다.
1. 기저 사례: 더 고를 원소가 없는 경우 결과를 출력하거나, 개수 증가 후 return
2. 고를 수 있는 원소들의 집합을 순회하며 재귀 함수 호출

그렇다면 기저에서 boolean을 반환하여 여러 가능성 중에서 ~ 가능한 경우가 한 가지는 있더라 / 아예 안 되더라라는 재귀 함수는 어떻게 작성할까?

대표적인 예제 문제로 BOGGLE 문제가 있다.

// 코드 6.3 보글 게임판에서 단어를 찾는 재귀 호출 알고리즘

const int dx[8] = { -1, -1, -1,  1, 1, 1,  0, 0 };
const int dy[8] = { -1,  0,  1, -1, 0, 1, -1, 1 };

// 5*5의 보글 게임 판의 해당 위치에서 주어진 단어가 시작하는지를 반환
bool hasWord(int y, int x, const string& word) {

    // 기저 사례 1: 시작 위치가 범위 밖이면 무조건 실패
    if (y < 0 || y >= 5 || x < 0 || x >= 5) return false;
    // 기저 사례 2: 첫 글자가 일치하지 않으면 실패
    if (board[y][x] != word[0]) return false;
    // 기저 사례 3: 단어 길이가 1이면 성공
    if (word.size() == 1) return true;
    
    // 인접한 여덟 칸을 검사한다.
    for (int direction = 0; direction < 8; ++direction) {
        int nextY = y + dy[direction], nextX = x + dx[direction];
        // 다음 칸이 범위 안에 있는지, 첫 글자는 일치하는지 확인할 필요가 없다.
        if (hasWord(nextY, nextX, word.substr(1)))
            return true;
    }
    
    return false;
}

bool hasWord(가능성 중 하나) {
    기저 사례 최대한 자세히 (성공, 실패 등)
    
    for (a = 여러 가능성 중 하나) {
        if (hasWord(a))
            return true;
    }
    
    return false;
}

이러면 여러 가능성 중 되는 경우가 있는지, 없는지를 판독할 수 있다. (근데 관련된 문제는 직접 안풀어봐서 감이 잘 안 온다... 이 정도 정리하면 될 듯?)

2-6-5 재귀 함수 디버깅 Tip

재귀 함수 디버깅은 힘들다. 스택이 쌓였다가 빠지고~ 를 반복하며 예상할 수 없는 일이 많이 일어나기 때문! 여기서의 Tip은 {과 }를 적절히 활용하여 스택이 쌓이고 빠지고를 시각화하는 것이다.

...

void pickAndUpdateCnt(vector<pii>& pickedFriendPair, int numOfRestFriendPair) {
    // cout << "numOfRestFriendPair " << numOfRestFriendPair << endl;
    if (numOfRestFriendPair == 0) { cnt++;
    // cout << "cnt " << cnt << endl;
    return; }

    int startIndex = tailIndexPlusOneIncludingEmpty(pickedFriendPair);
    // cout << "startIndex " << startIndex << endl;
    
    for (int i = startIndex; i < sz(friendPair); ++i) {
        cout << "{" << "i " << i << " among " << sz(friendPair) << endl;
        if (isElementInPairNotExistInListOfPair(friendPair[i], pickedFriendPair)) {
            pickedFriendPair.push_back(friendPair[i]);
            pickAndUpdateCnt(pickedFriendPair, numOfRestFriendPair - 1);
            pickedFriendPair.pop_back();
        }
        cout << "i " << i << " among " << sz(friendPair) << "}" << endl;
    }

    return;
}

작성한 함수를 보면, 재귀 함수를 호출하기 직전과 직후에 (조금 뭐가 더 있긴 하지만) i의 값을 관찰하고자 할 때 직전에는 {를, 직후에는 }를 추가해주었다. 이는 결과 창을 볼 때 재귀 함수가 어떻게 진행되고 있는지 인지하는데 도움을 준다.

재귀 함수를 디버깅할 때에는 재귀 함수를 호출하기 직전과 직후에 {과 }를 적절히 사용하여 스택이 쌓이고 빠지고를 시각화한다.

3 구종만's Sol

3-1 구종만's 재정의

아직 짝을 찾지 못한 학생들의 명단이 주어질 때 친구끼리 둘씩 짝짓는 경우의 수를 계산하라!

3-2 구종만's 구현 (틀림)

// 코드 6.4 소풍 문제를 해결하는 (잘못된) 재귀 호출 코드

int n;
bool areFriends[10][10];

// taken[i] = i번째 학생이 짝을 이미 찾았으면 true, 아니면 false
int countPairings(bool taken[10]) {

    // 기저 사례: 모든 학생이 짝을 찾았으면 한 가지 방법을 찾았으니 종료한다.
    bool finished = true;
    for (int i = 0; i < n; ++i) if (!taken[i]) finished = false;
    if (finished) return 1;
    int ret = 0;

    // 서로 친구인 두 학생을 찾아 짝을 지어 준다.
    for (int i = 0; i < n; ++i) {
        for (int j = i+1; j < n; ++j) {
            if (!taken[i] && !taken[j] && areFriends[i][j]) {
                taken[i] = taken[j] = true;
                ret += countPairings(taken);
                taken[i] = taken[j] = false;
            }
        }
    }
    
    return ret;
}

3-3 구종만's 검증

위 코드에는 두 가지 문제점이 존재한다.

같은 학생 쌍을 두 번 짝지어 준다.
예) (0,1)과 (1,0)을 따로 세고 있다.
다른 순서로 학생들을 짝지어 주는 것을 서로 다른 경우로 세고 있다.
예) (0,1) 후에 (2,3)을 짝지어 주는 것과 (2,3) 후에 (0,1)을 짝지어주는 것은 완전히 같은 방법인데 다른 경우로 세고 있다.

3-4 구종만's 구현 (fixed) using 정규화

각 단계에서 남아 있는 학생들 중 가장 번호가 빠른 학생의 짝을 찾아준다.

가장 번호가 빠른 학생의 짝은 그보다 번호가 뒤일 수밖에 없기 때문에 (1,0)과 같은 짝은 나올 수 없다.
또한, 항상 번호가 가장 빠른 학생부터 짝을 짓기 때문에 (2,3), (0,1)의 순서로 짝을 지어줄 일도 없다.

// 코드 6.4 소풍 문제를 해결하는 재귀 호출 코드

int n;
bool areFriends[10][10];
// taken[i] = i번째 학생이 짝을 이미 찾았으면 true, 아니면 false
int countPairings(bool taken[10]) {
    // 남은 학생들 중 가장 번호가 빠른 학생을 찾는다.
    int firstFree = -1;
    for (int i = 0; i < n; ++i) {
        if (!taken[i]) {
            firstFree = i;
            break;
        }
    }
    // 기저 사례: 모든 학생이 짝을 찾았으면 한 가지 방법을 찾았으니 종료한다.
    if (firstFree == -1) return 1;
    int ret = 0;
    // 이 학생과 짝지을 학생을 결정한다.
    for (int pairWith = firstFree + 1; pairWith < n; ++pairWith) {
        if (!taken[pairWith] && areFriends[firstFree][pairWith]) {
            taken[firstFree] = taken[pairWith] = true;
            ret += countPairings(taken);
            taken[firstFree] = taken[pairWith] = false;
        }
    }
    return ret;
}

3-5 구종만's 검증

답의 수의 상한

모든 답을 생성하며 답의 수를 세는 재귀 호출 알고리즘은 답의 수에 정비례하는 시간이 걸린다.

이 문제에서 가장 많은 답을 가질 수 있는 입력은 열 명의 학생이 모두 서로 친구인 경우이다. 이때 가장 번호가 빠른 학생이 선택할 수 있는 짝은 9명이고, 그 다음 학생이 선택할 수 있는 짝은 일곱 명이다.

따라서, 최종 답의 개수는 9x7x5x3x1 = 945 가 된다

3-6 구종만's Sol을 읽고 또 회고

3-6-1 입력 형태

나는 보자마자 친구 쌍 관계를 순서쌍 벡터에 저장할 생각을 했는데, 2차원 배열에 넣는 것도 좋은 방법인 것 같다. boolean 2차원 배열에 관계를 넣고 문제를 해결하다 보니.. 이 방법이 내 것보다 훨씬 간편한 것 같다. 내 방법은 관계가 선택되었는지 아닌지를 중심으로 재귀를 했고, 종만 씨는 사람이 택해졌는지 아닌지를 중심으로 재귀를 했다.

3-6-2 정규화

앞서 "누구끼리 친구인지에 대한 정보": (a, b)와 (b, a)는 동일한 정보이다. 이 단서를 더 멋있게 처리하고 싶었는데, 해당 풀이에서는 그 점을 인지하고 바로 처리한게 좋은 것 같다.

3-6-3 답의 상한 (시간복잡도)

내가 앞서 분석한 시간 복잡도는 틀리진 않았다. 하지만 이 문제의 경우 답의 상한이 비교적 작기 때문에 직접 계산하여 검증할 수 있었다. 이것이 중요한 이유는 내가 계산한 시간 복잡도가 터무니 없이 작게 나왔기 때문이다. 시간 복잡도 방식에 너무 의존하지 말고, 직접 계산하여 검증하는 습관을 익히자.

4 끝..?

종만: "한 번 푼 문제를 다시 본다고 해서 배우는 것이 있을까 생각할 수도 있지만, 오히려 문제를 한 번만 풀어서는 그 문제에서 배울 수 있는 것들을 다 배우지 못하는 경우가
더 많습니다."

다시 보고, 또 다시 보자!

Daniel Oh

안녕하세요. 오도열입니다.

이전 포스트

[알고리즘 문제 해결 전략] 02 문제 해결 개관

다음 포스트

[알고리즘 문제 해결 전략] 06.3 문제: 소풍 (문제 ID: PICNIC)