문제
프로그래머스 - 소수 찾기
🔢 문제 링크입니다! 🔢
문제 풀이
알고리즘 시나리오입니다!
1. n의 숫자들로 만들어질 수 있는 수를 전부 생성한다.
2. 각 숫자가 소수인지 확인하고 아니라면 삭제한다.
3. 남은 원소들의 갯수 반환하면 끝!
정답 보드를 돌아다니다가 발견한 끝판왕 답변을 먼저 공유드립니다.
def solution(n):
primes = set()
# 1단계
for i in range(len(n)):
primes |= set(map(int, map("".join, permutations(list(n), i+1))))
# 2단계
primes -= set(range(2))
for i in range(2, int((max(primes))**0.5) + 1):
primes -= set(range(i*2, max(primes) + 1, i))
# 3단계
return len(primes)간단히 부연설명을 해보자면, 주석으로 적어둔 1단계에서는 permutations 함수로 가능한 모든 숫자를 생성합니다.
set을 사용해서 중복되는 값들도 없애고, 합집합과 차집합을 사용했습니다!
그리고 2단계에서는 소수들을 지워나갑니다. 먼저 0, 1을 먼저 삭제하고, 에라토스테네스의 체를 이용해서 남은 숫자들을 지워줍니다.
마지막으로 남아있는 숫자들의 갯수를 반환합니다.
정말 간단하면서 코드가 술술 읽히는 대망의 답변인 것 같습니다.
이해에 도움이 될까싶어 위의 코드에서 소수를 찾아가는 과정을 프린트로 찍어봤습니다.
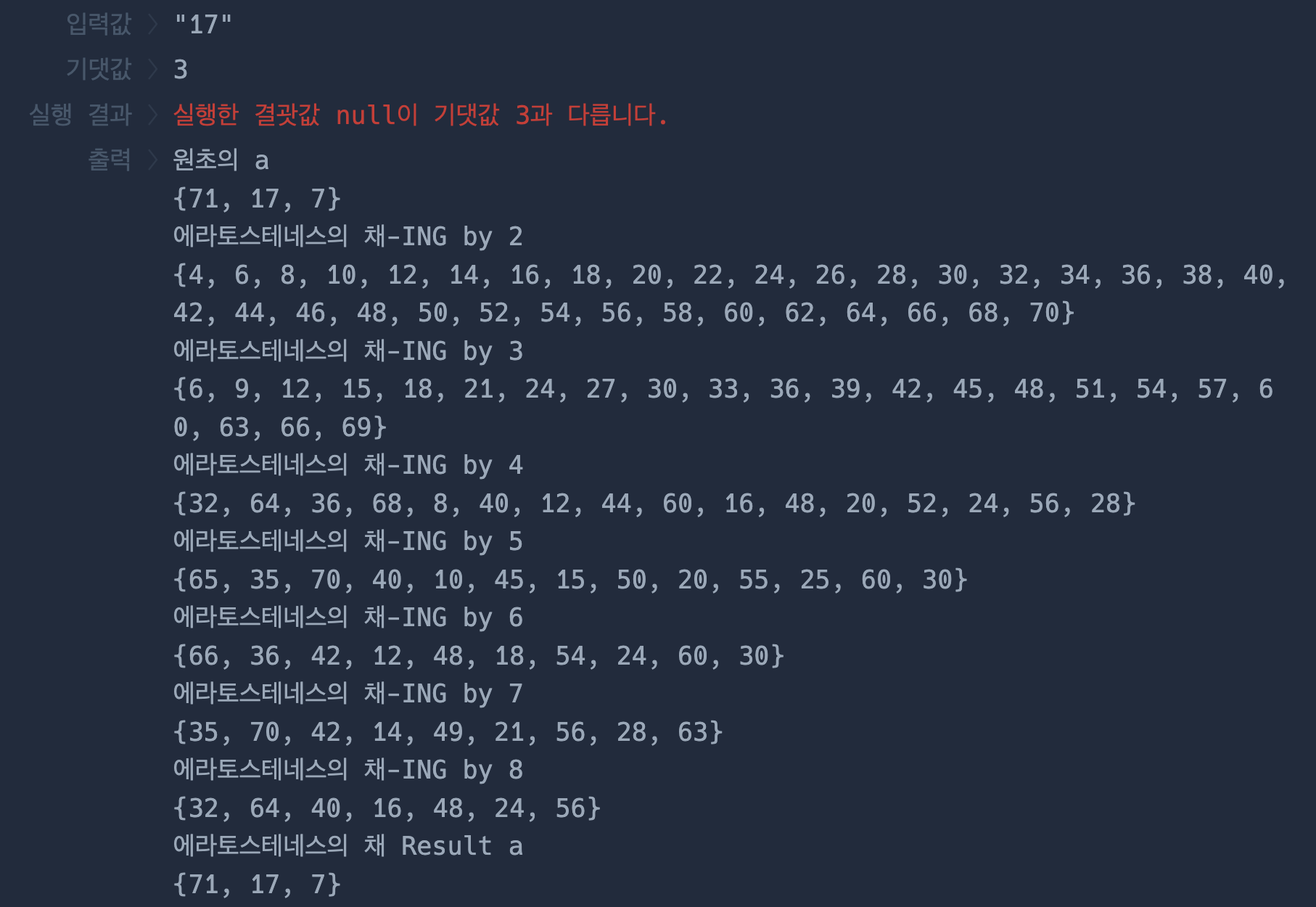
어떤가요? 원초의 숫자들에서 에라토스테네스의 체로 걸러지는 과정이 잘 보이지 않나요?
안타깝게도 위의 예시에서는 하나도 걸러지지 않았지만요...
🧏 이번 문제를 해결하면서 함께 알아가면 좋을 정보들을 정리해봤습니다!
에라토스테네스의 체
임의의 자연수 n에 대해 그 이하의 소수를 모두 찾는 방법입니다. 특히 소수를 대량으로 찾을 때 유용한 방법입니다.
과정은 다음과 같습니다.
1. 1부터 n을 원소로 갖는 배열 arr를 선언합니다.
2. 소수도 합성수도 아닌 자연수 1을 제거합니다.
3. 2부터 √n까지 돌면서 자기 자신을 제외한 배수를 제거합니다.
3번 과정에서 √n까지만 도는 이유는 각 수가 갖는 약수가 해당 수의 제곱근을 기준으로 대칭을 이루기 때문입니다.
예를 들어 16의 경우 1,2,4,8,16의 약수를 갖고 있습니다.
16의 양의 제곱근인 4를 기준으로 대칭을 이루기 때문에 소수가 아니라면 4가 나오기 전에 2로 나눠질 수 밖에 없습니다.
또 자기 자신을 제외한 배수를 제거한다는 것은 2나 3으로 나누어 떨어질 때 2와 3은 삭제되어서는 안 된다는 것입니다.
이 문제에 적용한 코드는 다음과 같습니다.
# 각 수가 갖는 약수는 해당 수의 제곱근을 기준으로 대칭을 이루므로 제곱근까지만 확인한다.
for i in range(2, int((max(primes))**0.5) + 1):
# 자기 자신은 지워지면 안 되니까 i*2부터!
primes -= set(range(i*2, max(primes) + 1, i))i*2부터 i씩 더하면서 배수를 찾아나가므로 자기 자신은 삭제되지 않을 것입니다.
map()
map()은 반복 가능한 자료형에 함수를 적용시켜서 반환해주는 함수입니다.
map(function, iterable)
위와 같은 형태이며 적용시킬 함수와 적용할 값이 들어간 iterable을 차례로 넣으시면 됩니다.
연산이 끝나고 map을 리턴하므로 적당한 자료형으로 변환하여 사용합시다.
이 문제에 사용한 예는 다음과 같습니다.
primes |= set(map(int, map("".join, permutations(list(n), i+1))))위의 코드는 permutation한 결과인 tuple을 하나의 String으로 만들고, int로 변환하여 primes에 추가하는 부분입니다.
tuple을 String으로 만들기 위해서 "".join 함수를 적용하고, int로 변환하기 위해 int 함수를 map했습니다.
하나씩 for문으로 돌면서 변환했다면 코드가 더 길어졌겠지만, map을 활용하니 한 줄로 정리가 가능합니다.
range()
range()는 일정 범위의 연속된 정수를 생성하는 함수입니다.
주로 for문과 함께 쓰여서 낯설게 느껴질 수 있지만 range 자체로도 사용할 수 있습니다.
예를 들어 range(1, 11) 라고 한다면 1부터 10까지의 정수를 생성하고 이를 range 객체로 반환합니다.
이를 list() 함수나 set()으로 변환하여 사용할 수 있습니다.
이번 문제를 푸는 과정에서 다음과 같이 사용되었습니다.
primes -= set(range(i*2, max(primes) + 1, i))이렇게 range를 이용해서 정수 작업을 하면, 한 줄로 에라토스테네스의 채를 구현할 수 있습니다.
filter()
filter()는 이름 그대로 필터링해주는 함수입니다.
filter(function, iterable)
map 함수와 비슷해보이지만 filter 함수가 받는 function은 True/False를 리턴해야 합니다.
iterable의 원소들을 순회하면서 function 함수를 적용시키고, True인 애들만 골라서 반환해줍니다.
filter() 또한 iterable로 리턴해주기 때문에 원하는 타입으로 변환하여 사용합시다.
이번 문제에 사용된 예시입니다.
return len(list(filter(is_prime, primes)))소수인지 판단하는 함수와 가능한 모든 수를 담은 primes 배열을 filter()로 보내서 소수인 숫자만 return되게 합니다.
permutations()
파이썬이 만들어준 순열 함수입니다.
tuple들의 list를 반환합니다.
from itertools import permutations
list = [1,2,3]
perm = permutations(list)
print(list(perm))
# print된 결과
[(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)]permutations()에 순열로 만들고 싶은 iterable을 인자로 넘겨줍니다.
두번째 인자로 길이를 지정할 수 있습니다. 만약 길이를 지정하지 않는다면 기본값으로 iterable의 길이를 사용합니다.
순서가 상관없는 조합을 사용한다면 combinations()를 사용합니다.
소스 코드
2가지 방법이 있습니다!
Method 1: set, map, range, 그리고 permutations 함수를 활용한 방법
Method 2: 재귀와 filter를 사용한 방법
from itertools import permutations
# Method 1: set, map, range, 그리고 permutations 함수를 멋지게 활용한 방법
def solution(n):
primes = set()
for i in range(len(n)):
primes |= set(map(int, map("".join, permutations(list(n), i+1))))
primes -= set(range(2)) # 0, 1 제외
# 각 수가 갖는 약수는 해당 수의 제곱근을 기준으로 대칭을 이루므로 제곱근까지만 확인한다.
for i in range(2, int((max(primes))**0.5) + 1):
# 자기 자신은 지워지면 안 되니까 i*2부터!
primes -= set(range(i*2, max(primes) + 1, i))
return len(primes)
# Method 2: 재귀와 filter를 사용한, 기본에 충실한 방법
def is_prime(n):
if n < 2:
return False
if n == 2:
return True
for i in range(2, int(n ** 0.5) + 1):
if (n % i) == 0:
return False
return True
primes = set()
def permutation(base, array):
if base:
primes.add(int(base))
for i, num in enumerate(array):
permutation(base + num, array[:i] + array[i+1:])
def solution(n):
permutation("", list(n))
return len(list(filter(is_prime, primes)))