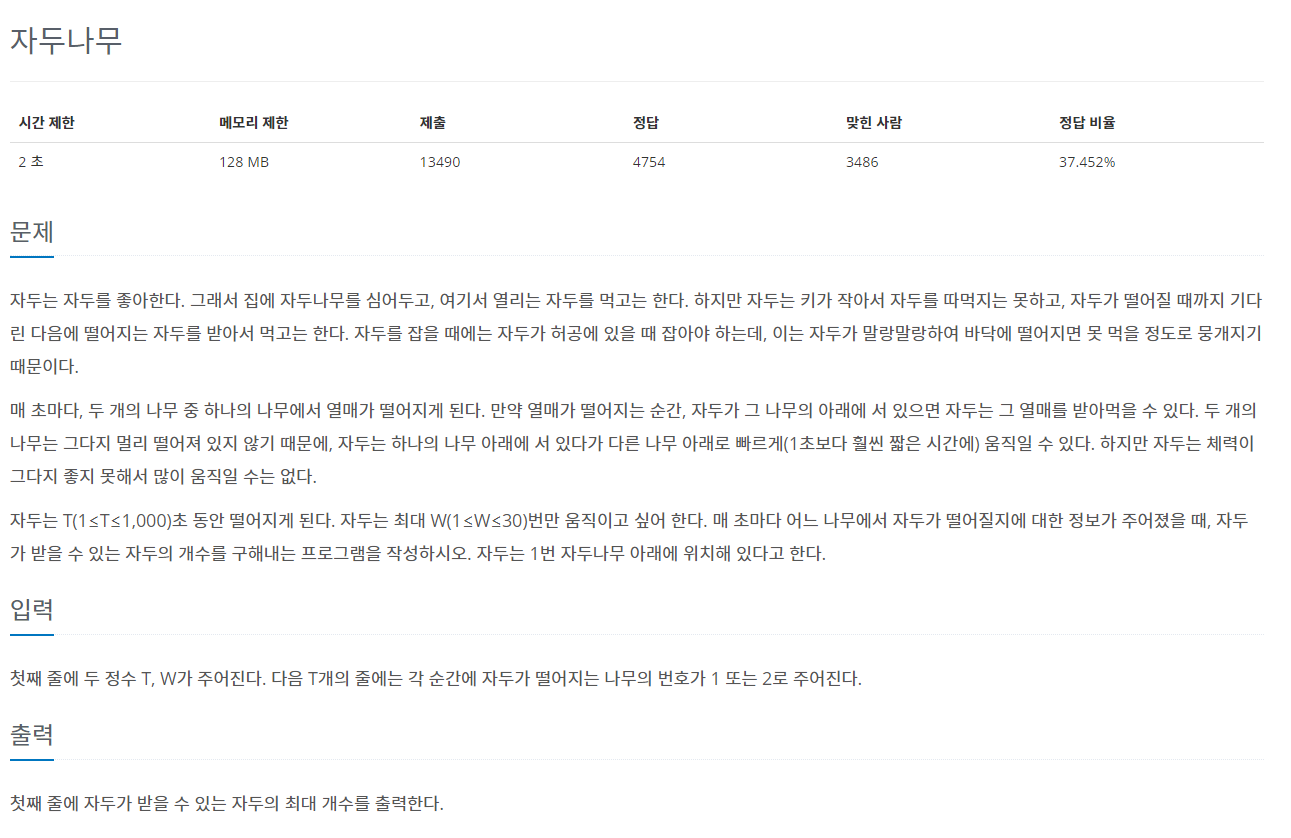
문제
비하인드 스토리
혼자 힘으로는 풀지 못해서 다른 이의 풀이를 참고해서 풀었는데 막상 스터디원들에게 설명하려니 내가 완전히 이해하지 못하고 있는 걸 알게 되어 더 분석해보기로 약속했다
풀이
dp를 사용했다. 보통 dp의 변수가 2개인 것에 반해서 여기서는 3개의 변수가 사용된다.
dp[자두나무][현재시간][움직인 횟수]
어려웠던 점
마지막 움직인 횟수부분이 날 어렵게 만들었다. 저기에 어떤 수가 적혀 있는 것이 특정 경로들을 지나와서 만들어지는 정보로 보여지지 않았다.
최단거리 알고리즘과 비교
그런데 생각해보니 다른 최단 거리 알고리즘들도 따로 경로를 저장하지 않으면 어떤 경로를 지나왔는지는 알지 못한다. 다만 그 변수, 혹은 위치에 도달하기까지의 최단거리를 갱신하는 식으로 이루어진다.
특정 시점에 취할 수 있는 선택지들을 계산하고 그 중 최소값을 갱신해나간다.
현재 문제에 적용
이 문제에서는 주어진 변수에서 취할 수 있는 최대 자두의 갯수를 구해야 한다. 그런데 움직이는 횟수의 제약이 있다. 우리는 횟수정보를 기록해야 한다.
횟수정보를 기록하는 두가지 방법
첫번째는 dfs, 백트래킹, 재귀처럼 매개변수로 기록해나가는 방식이다. 이것은 횟수가 맥시멈이 되면 초기화되고 저장할 값을 dp에 담아줄 것이다.
두번째는 지금처럼 for문을 이용하는 방법이다. 이 방법의 특징은 움직임횟수를 늘여가는 방식이 아닌 가능한 움직임의 경우의 수를 배열로 만들어 들어오는 값 자체를 제한함으로써 초기화가 없이 이어져나가게 하는 방식이다.
즉, 내가 처음에 생각했던 '구하고자 하는 dp의 값이 최대움직임 값을 지키며 이동했다는 것을 어떻게 알지?' 애초에 들어오는 값을 제한해서 가능한 것이다.
직접 두 눈으로 보자

노드그래프와 DP
나는 두 가지를 조금 다르게 생각했는지도 모르겠다. 보통 접했던 dp문제는 움직일 수 있는 능력에 초점을 맞췄다. 맵에서 장애물이나 제한이 있었지만 맵은 그저 놓여있는 것이었다.
반대로 노드는 맵자체에 움직일 수 있는 제한이 있다. 그래서 두 문제의 풀이방법을 다르게 생각했던 것 같다.
그런데 전에 접했던 맵을 통과하는 문제들도 사실 가상의 엣지들로 연결되어 있다. 그 정보들을 따로 저장하는 것이 불필요해서 없었던 것이다. 맵문제는 이동규칙에 의해서 엣지가 자동으로 생성되는 반면 그래프 문제들은 설계자에 의해서 미리 계획된 것이기 때문에 맵정보가 반드시 필요하다.
이 문제를 그래프에서 많이 사용되었던 최단거리 문제와 비교하여 보았을 때 규칙에 의해 가상의 엣지들이 존재하고 dp는 그 가상엣지들로부터 최대값을 저장하는 것이다.
올 수 있는 경우의 수 중에 가장 큰 수를 저장한다
이전 노드 접근
이건 조금 부끄러운 얘긴데 dp를 쌓아가면서 변수를 i + 1해주는 건 익숙했지만 이전 dp에 있는 값을 가져오는 i-1의 방식은 익숙하지 않았다.
이건 시점의 차이다
미래의 정보를 업데이트 하고 싶을 때는 i + 1 을 사용하고
지금의 정보를 업데이트 할 때는 i - 1 을 통해 가져와야 한다
빼준다 vs 이전노드
dp[1][i - 1][j - 1]
이 부분에서 i-1, j-1을 시간을 뺀다, 움직일 수 있는 횟수를 뺀다고 생각하고 있었다. 지금 다시 보니 얼마나 잘못 이해하고 있었는 지 보인다. 이 부분은 이전 노드에 대한 접근이다.
이해하고 난 후 수정코드
내가 이 문제를 이해한 방식을 더 잘 표현하고 있다
역활 나누기
내가 이 문제에서 헷갈렸던 '올 수 있는 경우의 수 중 가장 큰 수'의 개념이 잘 보이도록 코드를 구성했다.
핵심코드부분
for (int i = 1; i <= t; i++) {
int appleTree = arr[i];
for (int j = 1; j <= w + 1; j++) {
if (appleTree == 2 && i == 1 && j == 1) continue;
dp[1][i][j] = max(dp[1][i - 1][j], dp[2][i - 1][j - 1]); //가능한 전 노드 중 최대값을 갱신
dp[2][i][j] = max(dp[1][i - 1][j - 1], dp[2][i - 1][j]); //가능한 전 노드 중 최대값을 갱신
dp[appleTree][i][j]++;
}
}for문 w+1까지 해주는 이유
j-1을 가져오는 경우에서 0부터 for문을 시작하면 -1이 되어 오류가 발생한다. 그래서 idx자체를 1씩 증가시켜주는 것이다. 나중에 찾을 때 값-1해서 찾기도 하지만 이 문제에서는 봐야하는 dp값 중 최대값만 찾으면 되기에 해당과정이 필요없다.
전체코드
#include <iostream>
#include <algorithm>
using namespace std;
//자두나무
int dp[3][1001][32];//자두나무 위치, 자두가 떨어지는 초, 움직인 횟수
int arr[1001]; //자두 떨어지는 나무 정보
void solve() {
int t; cin >> t;
int w; cin >> w;
int ans = 0;
for (int i = 1; i <= t; i++) {
cin >> arr[i];
}
for (int i = 1; i <= t; i++) {
int appleTree = arr[i];
for (int j = 1; j <= w + 1; j++) {
if (appleTree == 2 && i == 1 && j == 1) continue;
dp[1][i][j] = max(dp[1][i - 1][j], dp[2][i - 1][j - 1]); //가능한 전 노드 중 최대값을 갱신
dp[2][i][j] = max(dp[1][i - 1][j - 1], dp[2][i - 1][j]); //가능한 전 노드 중 최대값을 갱신
dp[appleTree][i][j]++;
}
}
for (int i = 1; i <= w + 1; i++) {
ans = max(ans, max(dp[1][t][i], dp[2][t][i]));
}
cout << ans;
}
int main() {
solve();
}결론
문제를 못 풀었을 때 다른 사람 풀이를 보고 공부하고 그대로 적는 경우가 많았는데 내 것으로 완전히 이해하고 내 '말'로 풀어 써야 진짜 내 것이 되는 것을 다시 느꼈다.
더불어 스터디에서 코드를 말로 설명하는 것이 나의 빈 곳을 발견하는 데 큰 도움이 되었다.
집요하게 질문해 준 스터디원들 감사!
