1. Bagging [Bootstrap aggregating]

1) 기본 과정

(1) 데이터셋으로부터 반복적으로 샘플 추출
(2) 각 bootstrap 샘플에 대해 base classifier를 학습
(3) test data를 활용하여 전체 base classifier를 예측
(4) 전체 base classifier의 예측값 중 다수결로 결과를 채택

2) 데이터셋 추출시 주의할 점 [왕왕중요]

• 복원 추출 (with replacement)

  • 뽑힌 데이터는 다시 그대로 제자리에
  • 매번 뽑을 때마다 전체 데이터에서 하나씩 추출
  • 이 성질 때문에 하나의 샘플 데이터셋에는 같은 데이터가 여러 개 뽑힐수도 !
    <-> 반대로 말하면 등장하지 않는 데이터도 있을 수 있다는 의미 !

• 모든 데이터가 뽑힐 확률은 항상 동일 (= uniform probability distribution)

• 각 bootstrap 샘플은 실제 데이터와 같은 크기를 가짐

  • 만약에 데이터가 n개다
    -> n번 복원 추출해서 하나의 bootstrap 샘플 데이터를 만드는 것
    -> 결국 n개의 행을 복원 추출로 뽑아 하나의 데이터셋을 생성한다는 의미
  • 이 과정을 base classifier 개수만큼 반복

• => 평균적으로 실제 데이터에서 약 63%의 데이터만이 사용됨

  $1-(1-1/N)^N = 0.632$
  • N이 충분히 크다고 가정
  • 각 base classifier마다 실제 데이터 중 약 63%의 데이터만 사용

3) Bagging 특징

• bias가 높은 모델을 모아 유연한 모델처럼 사용할 수 있다
  -> 근데 이건 어어엄청 특이 케이스
• base classifier의 variance를 낮춤으로써 오류를 개선
  • 반대로, base classifier가 높은 bias를 가지면, bagging은 성능을 향상시키기 어려움
    -> 왜냐면 ... training set이 보통 63%만 사용되니까

---

2. Boosting

1) 기본 과정

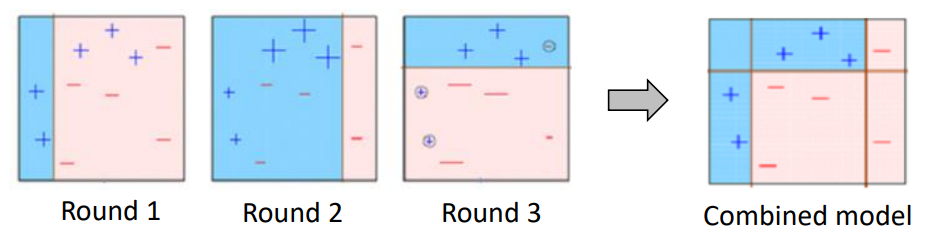
(1) 초기 가중치는 동일하게 $1/N$
(2) 샘플링 분포에 따라 샘플 추출
(3) 샘플 데이터를 가지고 훈련 -> original data에 대해 예측
(4) 가중치 조정

• 맞게 분류된 데이터의 가중치 -> 낮아짐
• 틀리게 분류된 데이터의 가중치 -> 높아짐
• 가중치가 높아졌다는 것은 다음 번 샘플링에서 뽑힐 확률이 높아진다는 의미
  & 틀렸을 때의 패널티가 더 크게 작용한다는 의미
  => 이전에 틀렸던 데이터를 더 잘 맞추려고 노력하게 만드는 것

2) Adaboost (boosting의 한 종류 / 대표적)

(1) boosting 알고리즘들을 구분하는 기준

• 각 라운드마다 가중치가 어떻게 업데이트되는가 ?
• 각 분류기로부터 만들어진 예측은 어떻게 결합되어 최종 결과를 내는가 ?

(2) 각 base classifier마다 error 계산법

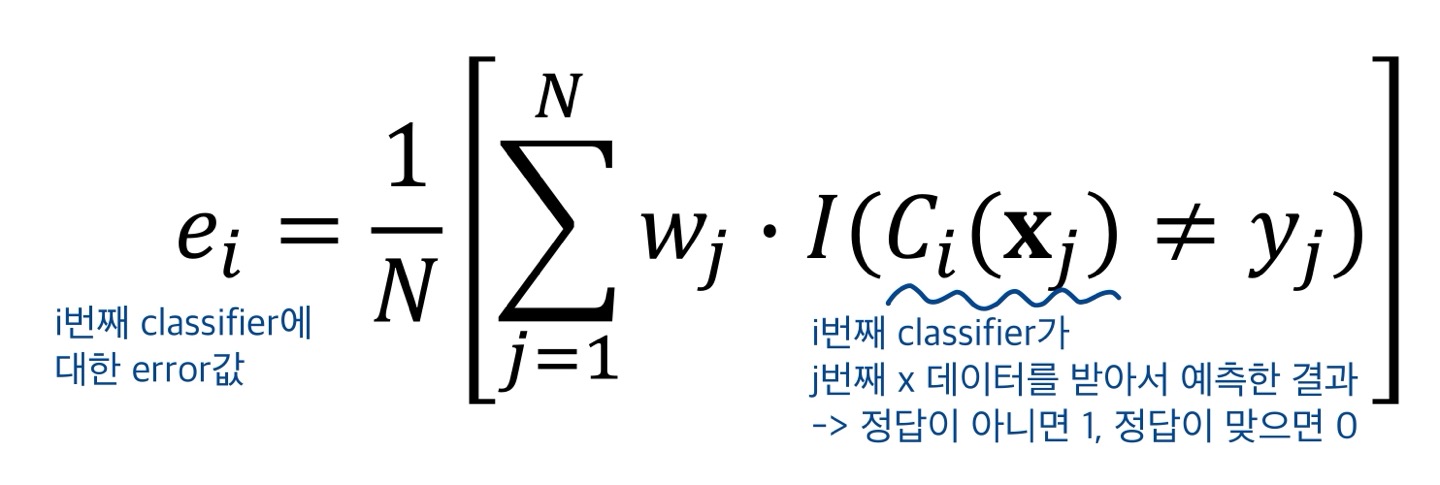
• $w_j$ : j번째 training example(= data object)의 가중치

(3) 각 base classifier마다 중요도 계산법

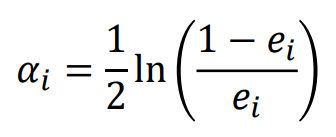
• $a_i$ : $i$번째 base classifier의 중요도
  -> 결과 결정시에 어떤 base classifier의 결과에 더 가중치를 주느냐를 결정하는데 사용
• $a_i$가 큰 양수값을 갖는다 -> error_rate는 0으로
• $a_i$가 큰 음수값을 갖는다 -> error_rate는 1로
• importance & error_rate => trade-off
• 보통 뒤에 실행된 모델일수록 importance 상승

(4) 각 training example마다 가중치 업데이트 방법

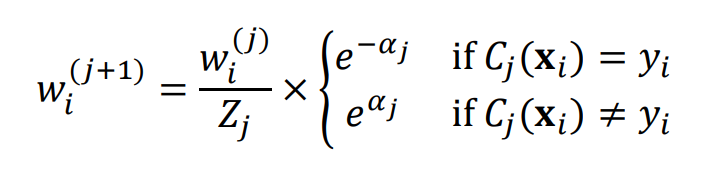
• $C_j(x_i) = y_i$ 정답을 맞췄을 때 -> $\times e^{-a_j}$
  -> 1보다 작은 값을 곱해 웨이트를 낮춰줌
• $C_j(x_i) \neq y_i$ 정답을 맞췄을 때 -> $\times e^{a_j}$
  -> 1보다 큰 값을 곱해 웨이트를 높여줌
• $a_j > 0$ 이라고 가정
  -> $e_j < 50$ 라고 가정하는 것과 같은 의미
• $Z_j$ : 가중치를 정규화 시켜주기 위한 값

(5) 최종 결과 생성법

• 성능이 낮을수록 낮은 중요도 -> 최종 결과에도 적게 영향을 미침
• 만약 오류율이 50% 이상이다 -> 가중치 초기화 -> $1/N$으로 돌아감

3) Boosting 특징

• Error rate가 매우 빠르게 수렴
• bias가 높은 애들을 사용해도 성능 효과가 있음
  • 왜냐면 앞의 과정에서 틀린 것들을 위주로 학습하기 때문에 bias가 높다 하더라도 통함
  • 모든 문제를 주는 것이 아니라 틀린 문제를 위주로 주기 때문에
  • variance를 낮춘다 = 하나의 결과에 좌지우지 되지 않는다 -> variance는 항상 낮춤
• 오버피팅의 가능성
  • 만약에 outlier같은 특이값이 들어왔는데 이걸 틀리게 분류했다면
  • 그다음에 이걸 맞추려고 여기에 가중치를 더 주고
  • 잘못된 값을 열심히 학습하게 됨
  • 잘못된 데이터의 특징을 지닌 모델이 나올 수 있음