서기 2012년! 드디어 2년간 수많은 국민들을 기다리게 한 게임 ACM Craft (Association of Construction Manager Craft)가 발매되었다.
이 게임은 지금까지 나온 게임들과는 다르게 ACM크래프트는 다이나믹한 게임 진행을 위해 건물을 짓는 순서가 정해져 있지 않다. 즉, 첫 번째 게임과 두 번째 게임이 건물을 짓는 순서가 다를 수도 있다. 매 게임시작 시 건물을 짓는 순서가 주어진다. 또한 모든 건물은 각각 건설을 시작하여 완성이 될 때까지 Delay가 존재한다.
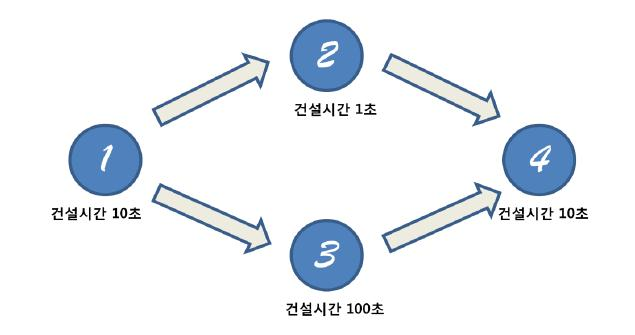
위의 예시를 보자.
이번 게임에서는 다음과 같이 건설 순서 규칙이 주어졌다. 1번 건물의 건설이 완료된다면 2번과 3번의 건설을 시작할수 있다. (동시에 진행이 가능하다) 그리고 4번 건물을 짓기 위해서는 2번과 3번 건물이 모두 건설 완료되어야지만 4번건물의 건설을 시작할수 있다.
따라서 4번건물의 건설을 완료하기 위해서는 우선 처음 1번 건물을 건설하는데 10초가 소요된다. 그리고 2번 건물과 3번 건물을 동시에 건설하기 시작하면 2번은 1초뒤에 건설이 완료되지만 아직 3번 건물이 완료되지 않았으므로 4번 건물을 건설할 수 없다. 3번 건물이 완성되고 나면 그때 4번 건물을 지을수 있으므로 4번 건물이 완성되기까지는 총 120초가 소요된다.
프로게이머 최백준은 애인과의 데이트 비용을 마련하기 위해 서강대학교배 ACM크래프트 대회에 참가했다! 최백준은 화려한 컨트롤 실력을 가지고 있기 때문에 모든 경기에서 특정 건물만 짓는다면 무조건 게임에서 이길 수 있다. 그러나 매 게임마다 특정건물을 짓기 위한 순서가 달라지므로 최백준은 좌절하고 있었다. 백준이를 위해 특정건물을 가장 빨리 지을 때까지 걸리는 최소시간을 알아내는 프로그램을 작성해주자.
이 문제를 처음에는 역 방향으로 돌려서 최대 시간이 걸리는
다익스트라를 써서 구현하려고 했지만 최장 시간은 다익스트라로 구할 수 없었다
왜냐하면 다익스트라는 양수 간선 하나라도 있으면 최장 시간을 구하는 로직에서
종료를 보장할 수 없기 때문이다 (이 부분에 대한 이해 필요)
이 문제를 수행할 때 DAG(비 순환 그래프)에서 순서가 보장 되어야 할 때
이를 Flat한 그래프로 만드는 알고리즘을 위상정렬이라고 한다.
문제의 핵심 과정은
1. 건설시간이 0초인 Node가 있다는 것
2. 진입 차수(inDegree)가 0인 출입 노드가 여러 개인 것
3. 앞선 차수들이 여러개일 때 그것을 해결 하지 않고는 대기열에 담길 수 없다는 것(Flat 조건)
4. 차수를 하나씩 제거해가면서 대기열에 넣을 수 있는
순서를 기다리며 DP 배열을 더 높은 cost 로 갱신시켜 가는 것.import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static int degree[];
static int N;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int T = Integer.parseInt(br.readLine());
while (T != 0) {
T--;
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int cost[] = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
// Make to graph
ArrayList<Integer> graph[] = new ArrayList[N + 1];
for(int i = 1; i <= N; i++) {
graph[i] = new ArrayList<>();
}
// 진입차수 배열
degree = new int[N+1];
// 1부터 n까지 더한값
int sum = N * (N + 1) / 2;
// graph 간선 설정
Set<Integer> set = new HashSet<>();
for(int i = 0; i < K; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
graph[from].add(to);
degree[to]++;
set.add(to);
}
// 도착점
int des = Integer.parseInt(br.readLine());
// 도착점이 진입차선이없다면
if(!set.contains(des)) {
System.out.println(cost[des-1]);
continue;
}
// 시작점은 진입차수 degree[i]의 num이 0인 곳
// 진입 점이 두 개일 수도 있다.
ArrayList<Integer> start = new ArrayList<>();
for(int i = 1; i <= N; i++) {
if(degree[i] == 0) {
start.add(i);
}
}
// 최소 비용
long r = topologySort(start, des, graph, cost);
System.out.println(r);
}
}
public static long topologySort(ArrayList<Integer> start, int des, ArrayList<Integer> graph[], int cost[]) {
long DP[] = new long[N+1];
// 0의 cost도 있기 때문에
Arrays.fill(DP, -1);
DP[des] = cost[des - 1];
// 시작에서 부터 queue에 넣는다
Queue<Node> queue = new LinkedList<>();
// 진입점들을 전부 넣어줘야함
for (int idx :start) {
queue.add(new Node(idx, cost[idx - 1]));
}
while(!queue.isEmpty()) {
Node nd = queue.poll();
// queue에서 꺼내고 진입 차수 제거
for(int idx :graph[nd.idx]) {
degree[idx]--;
if(DP[idx] < nd.cost + cost[idx - 1]) {
DP[idx] = nd.cost + cost[idx - 1];
}
if(degree[idx] == 0) {
queue.add(new Node(idx, DP[idx]));
}
}
}
return DP[des];
}
public static class Node {
int idx;
long cost;
public Node(int idx, long cost) {
this.idx = idx;
this.cost = cost;
}
}
}