2022 카카오 인턴 등산코스 정하기

XX산은 n개의 지점으로 이루어져 있습니다. 각 지점은 1부터 n까지 번호가 붙어있으며, 출입구, 쉼터, 혹은 산봉우리입니다. 각 지점은 양방향 통행이 가능한 등산로로 연결되어 있으며, 서로 다른 지점을 이동할 때 이 등산로를 이용해야 합니다. 이때, 등산로별로 이동하는데 일정 시간이 소요됩니다.

등산코스는 방문할 지점 번호들을 순서대로 나열하여 표현할 수 있습니다.
예를 들어 1-2-3-2-1 으로 표현하는 등산코스는 1번지점에서 출발하여 2번, 3번, 2번, 1번 지점을 순서대로 방문한다는 뜻입니다.
등산코스를 따라 이동하는 중 쉼터 혹은 산봉우리를 방문할 때마다 휴식을 취할 수 있으며, 휴식 없이 이동해야 하는 시간 중 가장 긴 시간을 해당 등산코스의 intensity라고 부르기로 합니다.

당신은 XX산의 출입구 중 한 곳에서 출발하여 산봉우리 중 한 곳만 방문한 뒤 다시 원래의 출입구로 돌아오는 등산코스를 정하려고 합니다. 다시 말해, 등산코스에서 출입구는 처음과 끝에 한 번씩, 산봉우리는 한 번만 포함되어야 합니다.
당신은 이러한 규칙을 지키면서 intensity가 최소가 되도록 등산코스를 정하려고 합니다.

다음은 XX산의 지점과 등산로를 그림으로 표현한 예시입니다.

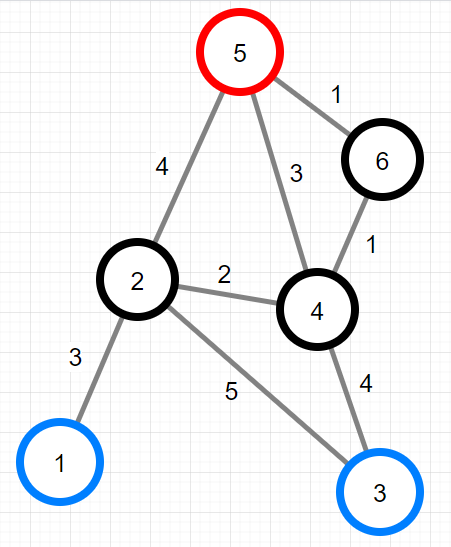
https://school.programmers.co.kr/learn/courses/30/lessons/118669

이 문제는 Gate의 수가 50000개라는 제한이 있다.
다시 말하자면 각 Gate를 다른 노드로 50000번 다익스트라를 실행
-> 시간초과

이 문제에서 요구하는 답은 '봉우리의 번호, 최소 intensity'
-> 출발지는 상관이 없다

결국 이 문제의 핵심은 모든 출입구를 하나의 다익스트라를 실행하여
각 노드들이 가질 수 있는 최소 intensity를 단조 증가하는 
최대 intensity를 갱신해주며 메모라이제이션 해주면 된다.

Max(현재까지의 간선 값, 다음 간선 값) < DP[다음 노드]
DP[다음노드] = Max(현재까지 간선 값, 다음 간선 값)

import java.util.*;
class Solution {
    
    public int[] solution(int n, int[][] paths, int[] gates, int[] summits) {
        int paLen = paths.length;
        int gateLen = gates.length;
        int summitLen = summits.length;
        ArrayList<Node>graph [] = new ArrayList[n+1];
        for(int i = 1; i <= n; i++) {
            graph[i] = new ArrayList<>();
        }
        HashSet<Integer> hs = new HashSet<>();
        for(int i : summits) {
            hs.add(i);
        }
        
        
        for(int i = 0; i < paLen; i++) {
            int from = paths[i][0];
            int to = paths[i][1];
            int cost = paths[i][2];
            
            graph[from].add(new Node(to, cost)); 
            graph[to].add(new Node(from, cost)); 
            
        }
           
        // 가장 큰 간선이 가장 작은...
        int DP[] = new int[n+1];
        Arrays.fill(DP, Integer.MAX_VALUE);
        
        // 단방향이고 큰 간선은 단조증가한다 지나온 간선보다 작은 간선은 지나온 간선 중 큰 간선과 swap
        Queue<Node> queue = new LinkedList<>();
        
        for(int i :gates) {
            queue.add(new Node(i, 0));
            DP[i] = 0;
        }
        while(!queue.isEmpty()) {
            Node tmp = queue.poll();
            if(hs.contains(tmp.cur)) {
                continue;
            }
            
            for(Node nd : graph[tmp.cur]) {
                if(Math.max(nd.edge, tmp.edge) < DP[nd.cur]) {
                    DP[nd.cur] = Math.max(nd.edge, tmp.edge);
                    queue.add(new Node(nd.cur, DP[nd.cur]));
                }
            }
            
            
        }
        
        
        
        int min = Integer.MAX_VALUE;
        int idx = 0;
        for(int i = 0; i < summitLen; i++) {
            if(min > DP[summits[i]]) {
                min = DP[summits[i]];
                idx = summits[i];
            } else if(min == DP[summits[i]]) {
                if(idx > summits[i]) {
                    idx = summits[i];
                }
            }
        }
        
        
        
        
        return new int[]{idx, min};
    }
    static class Node {
        int cur;
        int edge;
        public Node(int cur, int edge) {
            this.cur = cur;
            this.edge = edge;
        }
        
        
    }
}