특징점 추출 알고리즘

1. Harris corner [ 1988 ]
2. SIFT [ 2004 ]
3. FAST [ 2006 ]

영상 특징점이란?

영상에서 물체를 추적하거나 인식할 때, 영상과 영상을 매칭할 때 가장 일반적인 방법은 영상에서 주요 특징점을 뽑아서 매칭하는 것이다. 특징점을 영어로는 보통 keypoint 또는 interesting point라고 부른다.

영상에서 좋은 특징점은?

1. 물체의 형태나 크기, 위치가 변해도 쉽게 식별이 가능할 것
2. 카메라의 시점, 조명이 변해도 영상에서 해당 지점을 쉽게 찾아낼 수 있을 것

이러한 조건을 만족시키는 특징점은 코너점이다.

Harris Corner

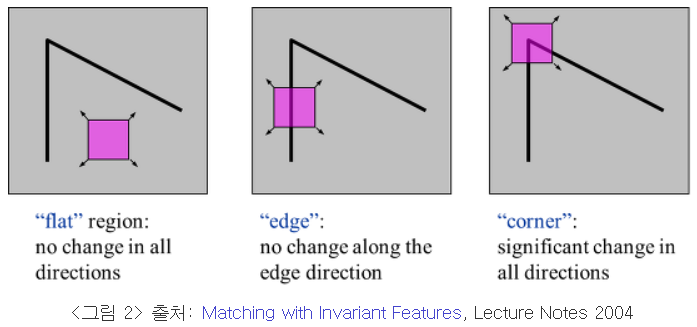
영상에서 코너를 찾는 기본적인 아이디어는 영상에서 작은 윈도우를 조금씩 이동시켰을 때, 코너점의 경우는 모든 방향으로 영상의 변화가 커진다.

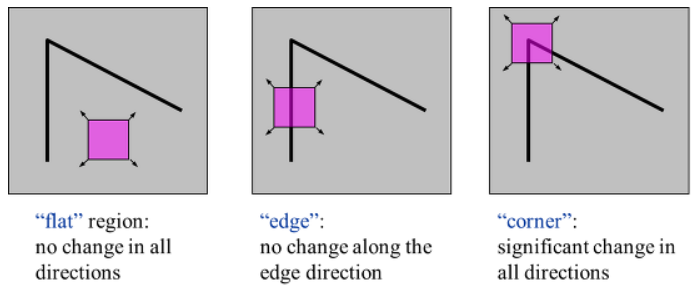
동작 원리

작은 윈도우를 수평, 수직, 좌대각선, 우대각선 4개 방향으로 1픽셀씩 이동시켰을 때 영상 변화량(SSD) E을 계산한 후, E들 중의 최소값을 해당 픽셀의 영상 변화량 값으로 설정, 이 최소값들 중 극대가 되는 지점을 코너점으로 함

특징

• 영상의 평행이동, 회전 변화에 불변
• affine 변화(카메라 각도에 의한 기하학 왜곡, 형태 변형 ) , 조명의 변화에도 어느 정도 강인하다.
• 영상 크기 변화에는 영향을 받는다. ( 적용할 때는 다양한 스케일을 고려해야할 수도 있다. )

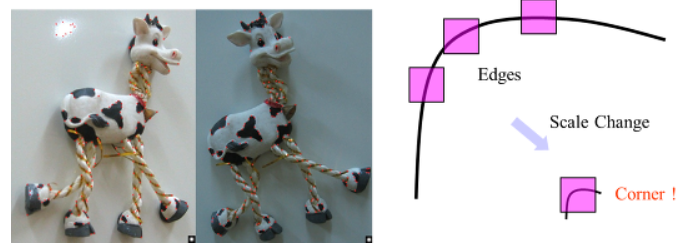
스케일 ( Scale )

영상인식, 컴퓨터 비전에서 스케일은 중요한 문제.

영상에서 물체의 특징을 계산할 때 어떤 스케일을 보느냐에 따라 전혀 다른 결과가 나올 수 있기 때문이다.

위와 같이 영상 코너 검출에서 큰 스케일에서는 명확히 코너점으로 인식되겠지만, 작은 스케일에서는 완만한 곡선 또는 직선으로 인식될 것이다.

• 스케일을 이미지 크기로 생각하기 쉬우나 서로 다른 개념이다.
  • 이미지 크기 : 이미지의 픽셀 수나 물리적인 width와 height
  • Scale : 이미지의 설명 ( 산의 모양을 본다면 scale이 큰 것이고 나뭇잎의 모양을 본다면 scale이 작은 것 )

SIFT

SIFT는 기존의 Harris 코너가 영상의 스케일 변화에 민감한 문제를 해결하기 위하여 DoG( Difference of Gaussian )를 기반으로 이미지 내에서 뿐만 아니라 스케일 축으로도 코너성이 극대인 점을 찾는다.

이미지 피라미드( Image Pyramid )

스케일에 불변하는 특징점을 찾기위해 고안된 방법

입력 이미지의 크기를 단계적으로 변화(축소)시켜 가면서 필요한 분석 작업을 한다.

ex ) 영상에서 보행자를 검출하는 경우, 이미지 피라미드를 생성한 후 각 스케일 영상에서 고정된 크기의 윈도우를 이동시켜 가면서 윈도우 내 영역이 보행자인지 여부를 판단.

SIFT에서 특징점을 추출하기 위해서 Laplacian 함수값을 사용한다. 각 영상 스케일마다 Laplacian 값을 계산하되 그 값이 이미지 내에서 뿐만 아니라 스케일 축으로도 극대( 또는 극소 )인 점들의 특징점으로 선택한다.

• Laplacian 계산은 이미지 밝기 변화에 대한 2차 미분값으로 계산되며, 영상 밝기 변화가 일정한 곳에서는 0에 가까운 값, 밝기가 급격한 곳에서는 높은 값(절대값)을 나타낸다.

실제 SIFT에서는 속도문제로 인해 Laplacian을 직접 계산하지 않고 DoG( Difference of Gaussian )를 이용하여 각 스케일별로 Laplacian을 근사적으로 계산한다.

DoG ( Difference of Gaussian )

입력 영상에서 Gaussian 필터를 점진적으로 적용하여 블러링시킨 이미지들에서 인접 이미지들간의 차 영상을 의미하며 이론적으로 LoG(Laplacian of Gaussian) 필터를 적용한 것과 거의 동일한 결과를 갖는다.

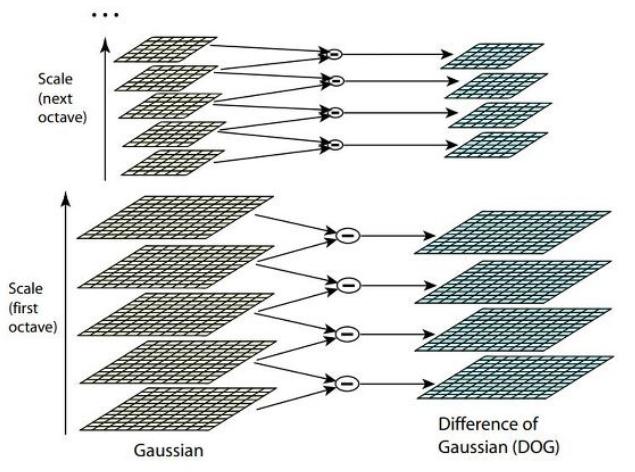
그렇게 얻어진 DoG 피라미드에서 극대 또는 극소점을 찾으면 SIFT의 특징점이 된다.

FAST

극도의 빠름을 추구한 특징점 추출 방법

속도에 최적화된 설계 기술임에도 특징점의 품질( repeatability : 다양한 영상 변화에서도 동일한 특징점이 반복되어 검출되는 정도 ) 또한 기존 방법을 상회한다.

FAST에서는 P를 중심으로하는 반지름 3인 원 상의 16개의 픽셀값을 보고 판단한다. P 값보다 일정값 이상( >P+t ) 밝은 픽셀들이 n개 이상 연속되어 있거나 일정값 이상 어두운 픽셀(< p - t )들이 n개 이상 연속되어 있으면 P를 코너점으로 판단한다.

FAST 알고리즘은 n을 몇 개 잡느냐에 따라서 FAST-9, FAST-10... 과 같이 다양한 버전이 가능하다.

어떤 점 P가 코너점인지 여부를 판단하기 위해 decision tree를 이용한다. 픽셀의 밝기값이 P보다 휠씬 밝은 경우, P보다 휠씬 어두운 경우, P와 유사한 경우 3가지 값으로 분류하고 원주상의 픽셀 밝기 분포를 16차원의 ternary 벡터로 표현한다. 이를 decision tree에 입력하여 코너점 분류한다.

non-maximal suppression

FAST 알고리즘은 어떤 점 P가 코너점으로 검출된 경우 P와 인접한 주변 점들도 같이 코너점으로 검출되는 경우가 많아지는 문제점이 있다. 이 문제를 해결하기 위해 코너성이 극대점만 남기고 나머지는 제거하는 방법이 non-maximal suppression이다.

FAST 알고리즘의 성능

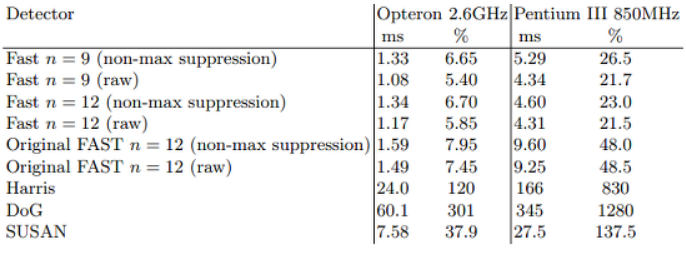
FAST - 9의 성능이 가장 좋으며 기존 방식에 비해 10배 이상의 속도 증가를 가져온다.

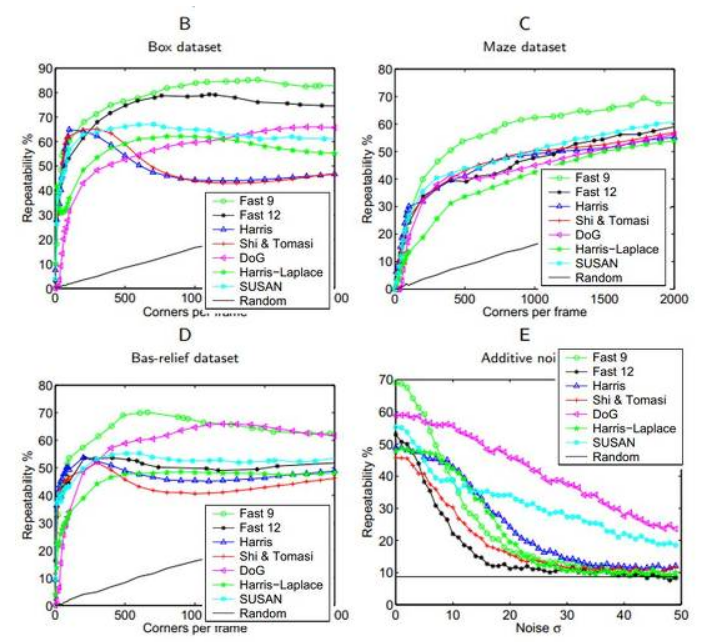
특징점의 품질(repeatability) 또한 기존 방법들을 상회하는 결과를 보여준다.